NRBSPHERETILE: Makes a quadrilateral NURBS tile of the unit sphere
from four vertex points.
Calling Sequence:
[tile] = nrbspheretile(ver3d)
INPUT:
ver3d: 3-by-4 matrix with the coordinates of 4 (ordered) vertices on
the sphere. Vertices should be ordered clockwise when viewed
from outside the sphere. The tile should be convex and should
contain the south pole.
OUTPUT:
tile: NURBS object representing the tile of the sphere. The tile
will be a quartic rational Bezier patch.
See also: nrbspheretiling
This function is based on the paper:
J.E. Cobb, Tiling the Sphere with Rational Bezier patches, 1988
For more details, see:
Sander Dedoncker, Laurens Coox, Florian Maurin, Francesco Greco, Wim Desmet
Bézier tilings of the sphere and their applications in benchmarking multipatch isogeometric methods
Computer Meth. Appl. Mech. Engrg., 2018
Copyright (C) 2017 Sander Dedoncker
This program is free software: you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation, either version 3 of the License, or
(at your option) any later version.
Demonstration 1
The following code
vertices = [1 -1 -1 1;1 1 -1 -1;-1 -1 -1 -1]/sqrt(3);
tile = nrbspheretile(vertices);
figure
nrbkntplot(tile)
title('Spherical cube tile')
Produces the following figure
| Figure 1 |
|---|
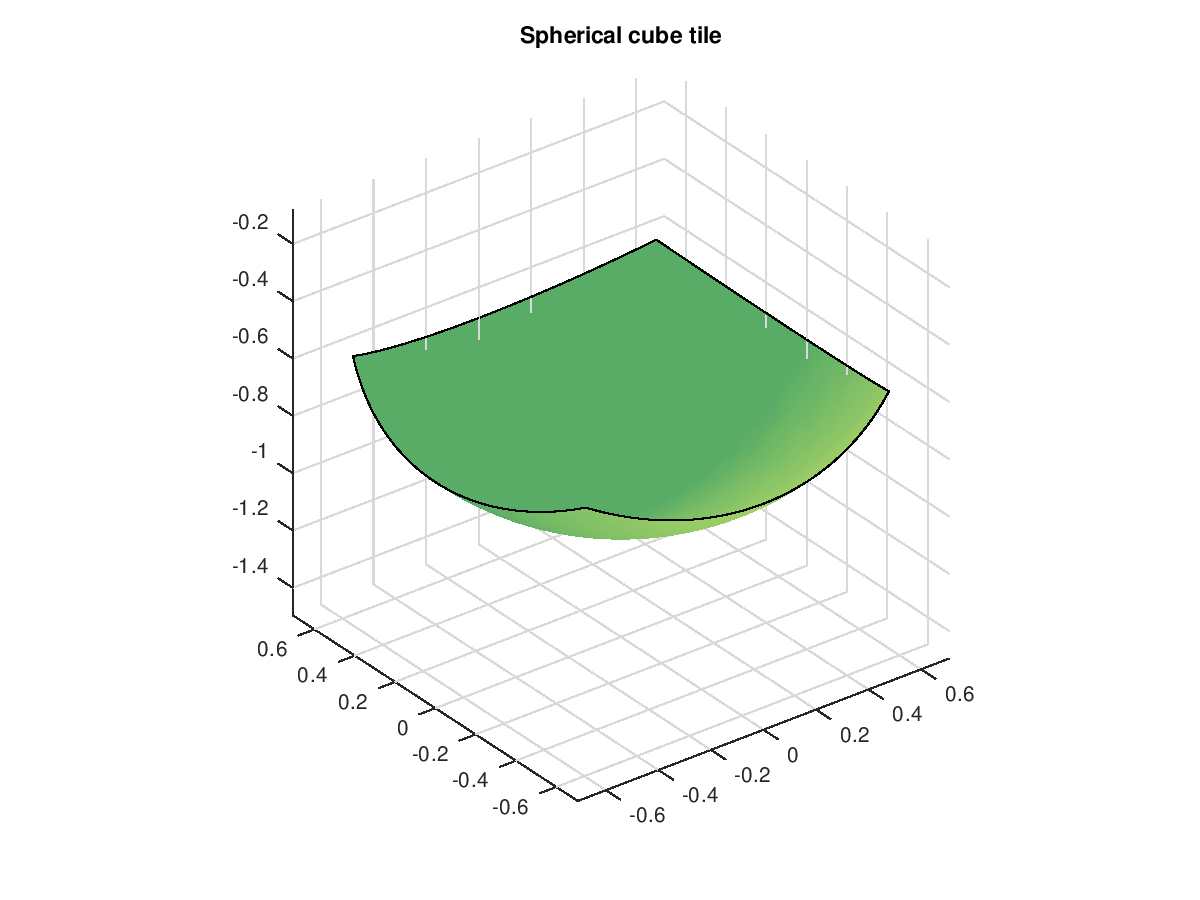 |
Demonstration 2
The following code
vertices = [0 1 sqrt(2)/2 0;0 0 sqrt(2)/2 1; -1 0 0 0] ;
tile = nrbspheretile(vertices);
figure
nrbkntplot(tile)
title('Single patch octant tile')
Produces the following figure
| Figure 1 |
|---|
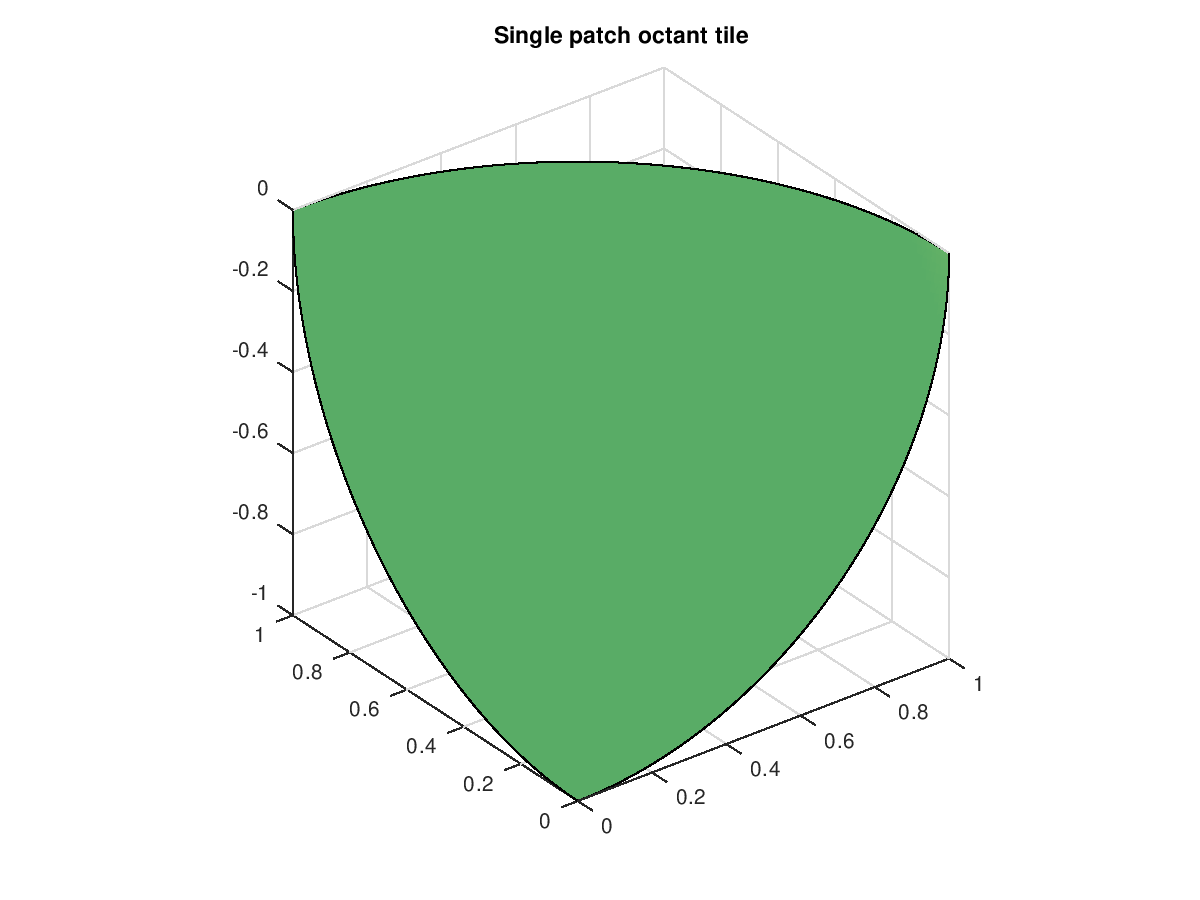 |
Package: nurbs