- : [p,details] = _oc_polybool(sub,clip)
- : [p,details] = _oc_polybool(sub,clip,op)
- : [p,details] = _oc_polybool(sub,clip,op,hor)
-
This function performs boolean operations between two polygons using the Greiner-Hormann algorithm as it is presented in http://davis.wpi.edu/~matt/courses/clipping/
sub is a two column matrix containing the X and Y coordinates of the vertices for the subject polygon (it must be unique, although self-intersections are permitted).
clip is a two column matrix containing the X and Y coordinates of the vertices for the clipper polygon(it must be unique, although self-intersections are permitted).
op is a text string containing the operation to perform between sub and clip. Possible values are:
- ’AND’ Intersection of sub and clip. This value is set by default.
- ’OR’ Union of sub and clip.
- ’AB’ Operation sub - clip.
- ’BA’ Operation of clip - sub.
- ’XOR’ Exclusive disjunction between clip and sub. This operation is performed as the joining of ’AB’ and ’BA’ consecutively applied
hor is an identifier for performing (value 1, by default) or not (value 0) the searching for holes in the result of the operation OR. When OR is applied with non convex entities some of the resulting polygons can be actually holes. Activating this argument the possible holes are identified. If the operation is other than OR the value of this argument is irrelevant
For the matrices sub and clip, the first point is not needed to be repeated at the end (but is permitted). Pairs of (NaN,NaN) coordinates in sub and/or clip are omitted, so they are treated as if each one stored a single polygon, i.e., this function does not admit boolean operations between multiple polygons of between polygons with holes, although polygons containing self-intersections are permitted
p is a two column matrix containing the X and Y coordinates of the vertices of the resultant polygon(s). If the result consist of multiple polygons they are separated by rows os (NaN,NaN) values.
details is a struct containing details of the computation. Its fields (IN LOWERCASE!) are:
- poly Three-column matrix with a number of rows equal to the number of polygons stored in the matrix p. The first column stores the row of p where the corresponding polygon starts, the second column the row of p where the polygon end, and the third colum is a mark identifying if the polygon is a hole (value 0) or not (value 1). The values of the third column are relevant only in the case of the OR operation
- nint Number of intersections between sub and clip.
- npert Number of perturbed points of the clip polygon if any particular case (points in the border of the other polygon) occurs see http://davis.wpi.edu/~matt/courses/clipping/ for details.
This function does not check if the dimensions of sub and clip are correct.
Demonstration 1
The following code
%subject polygon
clSub = [9.0 7.5
9.0 3.0
2.0 3.0
2.0 4.0
8.0 4.0
8.0 5.0
2.0 5.0
2.0 6.0
8.0 6.0
8.0 7.0
2.0 7.0
2.0 7.5
9.0 7.5];
%clipper polygon
clClip = [2.5 1.0
7.0 1.0
7.0 8.0
6.0 8.0
6.0 2.0
5.0 2.0
5.0 8.0
4.0 8.0
4.0 2.0
3.0 2.0
3.0 8.0
2.5 8.0
2.5 1.0];
%limits for the plots
clXLim = [1.5 11.75];
clYLim = [0.5 8.50];
%compute intersection
[pI,detI] = oc_polybool(clSub,clClip,'and');
%compute union
[pU,detU] = oc_polybool(clSub,clClip,'or',1);
%compute A-B
[pA,detA] = oc_polybool(clSub,clClip,'ab');
%compute B-A
[pB,detB] = oc_polybool(clSub,clClip,'ba');
%compute XOR
[pX,detX] = oc_polybool(clSub,clClip,'xor');
%plotting
figure(1);
%plot window for original data
subplot(3,2,1);
plot(clSub(:,1),clSub(:,2),clClip(:,1),clClip(:,2));
axis('equal');
xlim(clXLim);
ylim(clYLim);
title('Original polygons');
legend('Subject polygon','Clipper polygon','location','southeast');
%plot window for intersection
subplot(3,2,2);
hold('on');
for i=1:size(detI.poly,1)
pS = detI.poly(i,1);
pE = detI.poly(i,2);
fill(pI(pS:pE,1),pI(pS:pE,2),'r');
end
hold('off');
axis('equal');
xlim(clXLim);
ylim(clYLim);
title('OctCLIP intersection');
%plot window for union
subplot(3,2,3);
hold('on');
for i=1:size(detU.poly,1)
pS = detU.poly(i,1);
pE = detU.poly(i,2);
if detU.poly(i,3)~=0
fill(pU(pS:pE,1),pU(pS:pE,2),'r');
else
hax = fill(pU(pS:pE,1),pU(pS:pE,2),'b');
legend(hax,'Holes');
end
end
hold('off');
axis('equal');
xlim(clXLim);
ylim(clYLim);
title('OctCLIP union');
%plot window for A-B
subplot(3,2,4);
hold('on');
for i=1:size(detA.poly,1)
pS = detA.poly(i,1);
pE = detA.poly(i,2);
fill(pA(pS:pE,1),pA(pS:pE,2),'r');
end
hold('off');
axis('equal');
xlim(clXLim);
ylim(clYLim);
title('OctCLIP A-B');
%plot window for B-A
subplot(3,2,5);
hold('on');
for i=1:size(detB.poly,1)
pS = detB.poly(i,1);
pE = detB.poly(i,2);
fill(pB(pS:pE,1),pB(pS:pE,2),'r');
end
hold('off');
axis('equal');
xlim(clXLim);
ylim(clYLim);
title('OctCLIP B-A');
%plot window for XOR
subplot(3,2,6);
hold('on');
for i=1:size(detX.poly,1)
pS = detX.poly(i,1);
pE = detX.poly(i,2);
fill(pX(pS:pE,1),pX(pS:pE,2),'r');
end
hold('off');
axis('equal');
xlim(clXLim);
ylim(clYLim);
title('OctCLIP XOR');
%input message
disp('Press ENTER to continue ...');
pause();
%subject polygon
clSub = [1000.0 1000.0
2000.0 1000.0
2000.0 2800.0
800.0 2800.0
2400.0 1900.0
1000.0 1000.0];
%clipper polygon
clClip = [ 300.0 2500.0
2500.0 2600.0
1600.0 600.0
1300.0 3100.0
500.0 900.0
300.0 2500.0];
%limits for the plots
auxLim = [clSub;clClip];
clXLim = [min(auxLim(:,1)) max(auxLim(:,1))];
clYLim = [min(auxLim(:,2)) max(auxLim(:,2))];
%compute intersection
[pI,detI] = oc_polybool(clSub,clClip,'and');
%compute union
[pU,detU] = oc_polybool(clSub,clClip,'or',1);
%compute A-B
[pA,detA] = oc_polybool(clSub,clClip,'ab');
%compute B-A
[pB,detB] = oc_polybool(clSub,clClip,'ba');
%compute XOR
[pX,detX] = oc_polybool(clSub,clClip,'xor');
%plotting
figure(2);
%plot window for original data
subplot(3,2,1);
plot(clSub(:,1),clSub(:,2),clClip(:,1),clClip(:,2));
axis('equal');
xlim(clXLim);
ylim(clYLim);
title('Original polygons');
legend('Subject polygon','Clipper polygon','location','southeast');
%plot window for intersection
subplot(3,2,2);
hold('on');
for i=1:size(detI.poly,1)
pS = detI.poly(i,1);
pE = detI.poly(i,2);
fill(pI(pS:pE,1),pI(pS:pE,2),'r');
end
hold('off');
axis('equal');
xlim(clXLim);
ylim(clYLim);
title('OctCLIP intersection');
%plot window for union
subplot(3,2,3);
hold('on');
for i=1:size(detU.poly,1)
pS = detU.poly(i,1);
pE = detU.poly(i,2);
if detU.poly(i,3)~=0
fill(pU(pS:pE,1),pU(pS:pE,2),'r');
else
hax = fill(pU(pS:pE,1),pU(pS:pE,2),'b');
legend(hax,'Holes');
end
end
hold('off');
axis('equal');
xlim(clXLim);
ylim(clYLim);
title('OctCLIP union');
%plot window for A-B
subplot(3,2,4);
hold('on');
for i=1:size(detA.poly,1)
pS = detA.poly(i,1);
pE = detA.poly(i,2);
fill(pA(pS:pE,1),pA(pS:pE,2),'r');
end
hold('off');
axis('equal');
xlim(clXLim);
ylim(clYLim);
title('OctCLIP A-B');
%plot window for B-A
subplot(3,2,5);
hold('on');
for i=1:size(detB.poly,1)
pS = detB.poly(i,1);
pE = detB.poly(i,2);
fill(pB(pS:pE,1),pB(pS:pE,2),'r');
end
hold('off');
axis('equal');
xlim(clXLim);
ylim(clYLim);
title('OctCLIP B-A');
%plot window for XOR
subplot(3,2,6);
hold('on');
for i=1:size(detX.poly,1)
pS = detX.poly(i,1);
pE = detX.poly(i,2);
fill(pX(pS:pE,1),pX(pS:pE,2),'r');
end
hold('off');
axis('equal');
xlim(clXLim);
ylim(clYLim);
title('OctCLIP XOR');
Produces the following output
Press ENTER to continue ...
and the following figures
| Figure 1 | Figure 2 |
|---|---|
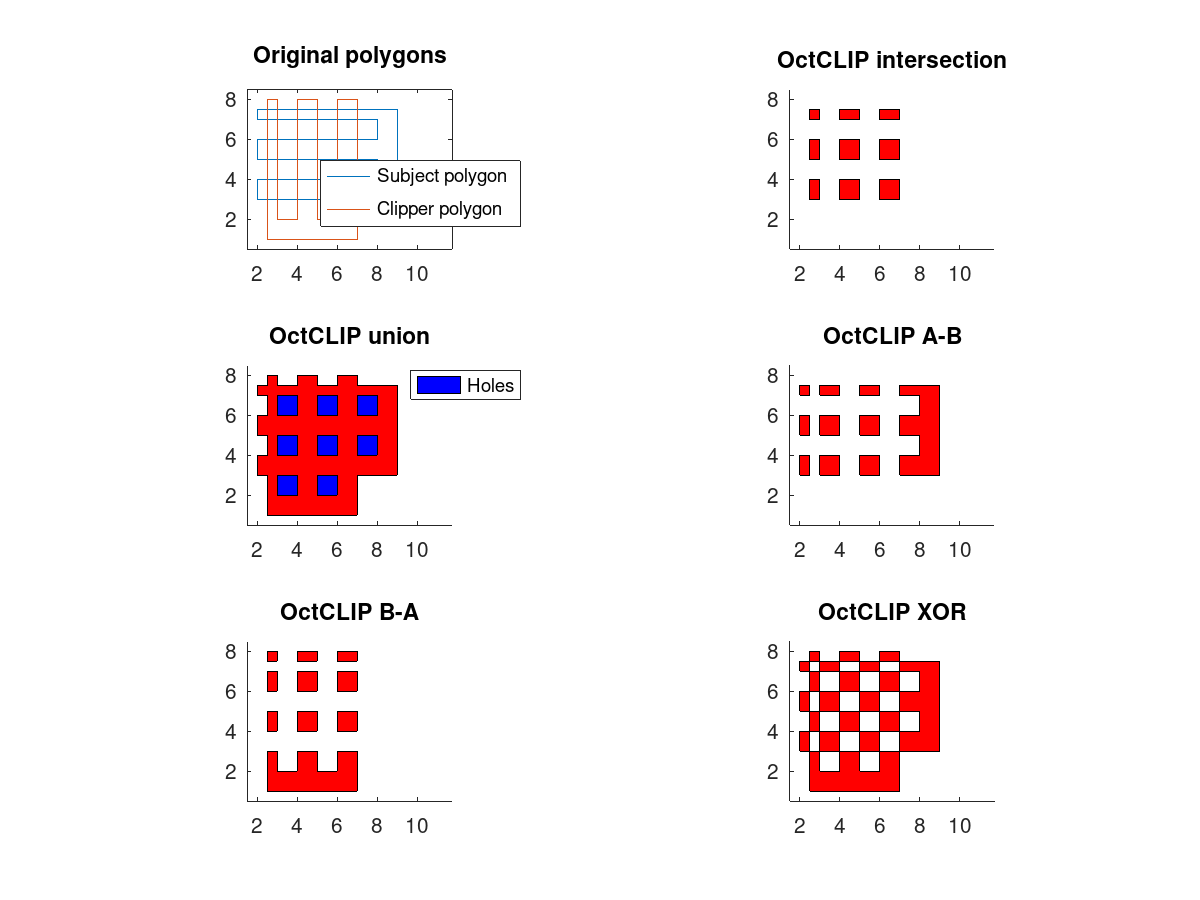 |
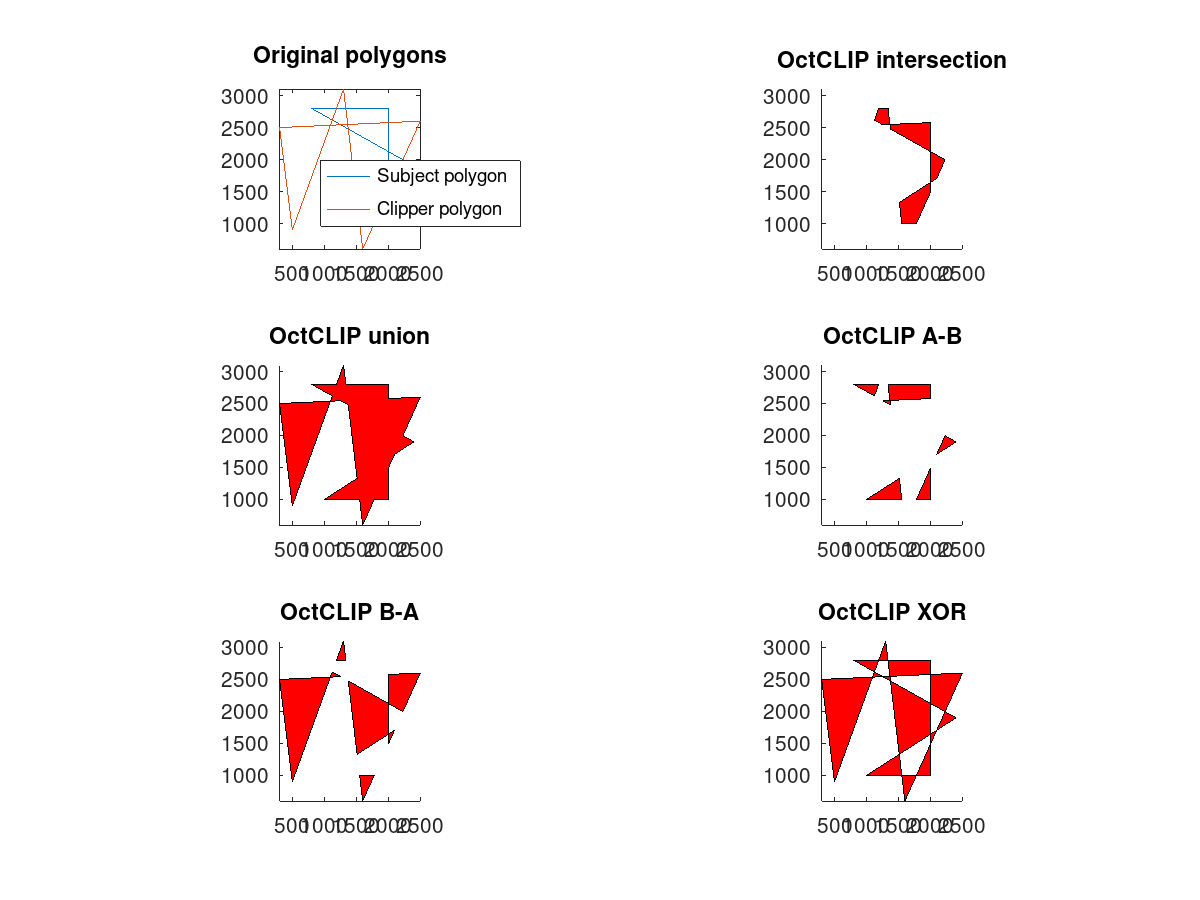 |
Package: octclip