de_min: global optimisation using differential evolution
Usage: [x, obj_value, nfeval, convergence] = de_min(fcn, control)
minimization of a user-supplied function with respect to x(1:D),
using the differential evolution (DE) method based on an algorithm
by Rainer Storn (http://www.icsi.berkeley.edu/~storn/code.html)
See: http://www.softcomputing.net/tevc2009_1.pdf
Arguments:
---------------
fcn string : Name of function. Must return a real value
control vector : (Optional) Control variables, described below
or struct
Returned values:
----------------
x vector : parameter vector of best solution
obj_value scalar : objective function value of best solution
nfeval scalar : number of function evaluations
convergence : 1 = best below value to reach (VTR)
0 = population has reached defined quality (tol)
-1 = some values are close to constraints/boundaries
-2 = max number of iterations reached (maxiter)
-3 = max number of functions evaluations reached (maxnfe)
Control variable: (optional) may be named arguments (i.e. "name",value
---------------- pairs), a struct, or a vector, where
NaN's are ignored.
XVmin : vector of lower bounds of initial population
*** note: by default these are no constraints ***
XVmax : vector of upper bounds of initial population
constr : 1 -> enforce the bounds not just for the initial population
const : data vector (remains fixed during the minimization)
NP : number of population members
F : difference factor from interval [0, 2]
CR : crossover probability constant from interval [0, 1]
strategy : 1 --> DE/best/1/exp 7 --> DE/best/1/bin
2 --> DE/rand/1/exp 8 --> DE/rand/1/bin
3 --> DE/target-to-best/1/exp 9 --> DE/target-to-best/1/bin
4 --> DE/best/2/exp 10--> DE/best/2/bin
5 --> DE/rand/2/exp 11--> DE/rand/2/bin
6 --> DEGL/SAW/exp else DEGL/SAW/bin
refresh : intermediate output will be produced after "refresh"
iterations. No intermediate output will be produced
if refresh is < 1
VTR : Stopping criterion: "Value To Reach"
de_min will stop when obj_value <= VTR.
Use this if you know which value you expect.
tol : Stopping criterion: "tolerance"
stops if (best-worst)/max(1,worst) < tol
This stops basically if the whole population is "good".
maxnfe : maximum number of function evaluations
maxiter : maximum number of iterations (generations)
The algorithm seems to work well only if [XVmin,XVmax] covers the
region where the global minimum is expected.
DE is also somewhat sensitive to the choice of the
difference factor F. A good initial guess is to choose F from
interval [0.5, 1], e.g. 0.8.
CR, the crossover probability constant from interval [0, 1]
helps to maintain the diversity of the population and is
rather uncritical but affects strongly the convergence speed.
If the parameters are correlated, high values of CR work better.
The reverse is true for no correlation.
Experiments suggest that /bin likes to have a slightly
larger CR than /exp.
The number of population members NP is also not very critical. A
good initial guess is 10*D. Depending on the difficulty of the
problem NP can be lower than 10*D or must be higher than 10*D
to achieve convergence.
Default Values:
---------------
XVmin = [-2];
XVmax = [ 2];
constr= 0;
const = [];
NP = 10 *D
F = 0.8;
CR = 0.9;
strategy = 12;
refresh = 0;
VTR = -Inf;
tol = 1.e-3;
maxnfe = 1e6;
maxiter = 1000;
Example to find the minimum of the Rosenbrock saddle:
----------------------------------------------------
Define f as:
function result = f(x);
result = 100 * (x(2) - x(1)^2)^2 + (1 - x(1))^2;
end
Then type:
ctl.XVmin = [-2 -2];
ctl.XVmax = [ 2 2];
[x, obj_value, nfeval, convergence] = de_min (@f, ctl);
Keywords: global-optimisation optimisation minimisation
Demonstration 1
The following code
## define a simple example function f = @(x) peaks(x(1), x(2)); ## plot the function to see where the minimum might be peaks() ## first we set the region where we expect the minimum ctl.XVmin = [-3 -3]; ctl.XVmax = [ 3 3]; ## and solve it with de_min [x, obj_value, nfeval, convergence] = de_min (f, ctl)
Produces the following output
x = 0.2285 -1.6253 obj_value = -6.5511 nfeval = 900 convergence = 0
and the following figure
| Figure 1 |
|---|
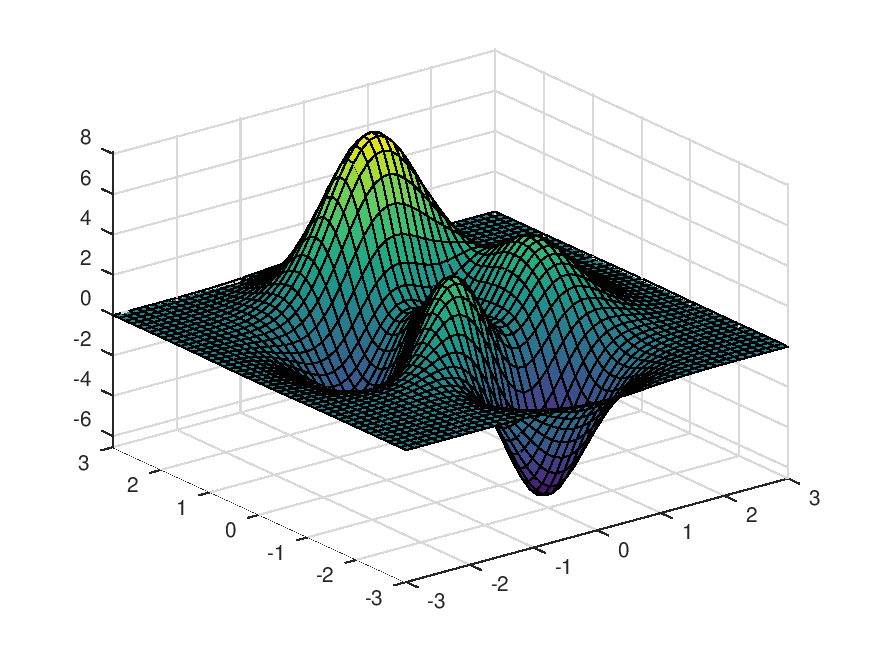 |
Package: optim