- Function File: M = ctmctaexps (Q, t, p0)
- Function File: M = ctmctaexps (Q, p0)
-
Compute the time-averaged sojourn time
M(i), defined as the fraction of the time interval [0,t] (or until absorption) spent in state i, assuming that the state occupancy probabilities at time 0 are p.INPUTS
Q(i,j)Infinitesimal generator matrix.
Q(i,j)is the transition rate from state i to state j, 1 ≤ i,j ≤ N, i \neq j. The matrix Q must also satisfy the condition \sum_{j=1}^N Q_{i,j} = 0tTime. If omitted, the results are computed until absorption.
p0(i)initial state occupancy probabilities.
p0(i)is the probability that the system is in state i at time 0, i = 1, …, N
OUTPUTS
M(i)When called with three arguments,
M(i)is the expected fraction of the interval [0,t] spent in state i assuming that the state occupancy probability at time zero is p. When called with two arguments,M(i)is the expected fraction of time until absorption spent in state i; in this case the mean time to absorption issum(M).
See also: ctmcexps.
Demonstration 1
The following code
lambda = 0.5;
N = 4;
birth = lambda*linspace(1,N-1,N-1);
death = zeros(1,N-1);
Q = diag(birth,1)+diag(death,-1);
Q -= diag(sum(Q,2));
t = linspace(1e-5,30,100);
p = zeros(1,N); p(1)=1;
M = zeros(length(t),N);
for i=1:length(t)
M(i,:) = ctmctaexps(Q,t(i),p);
endfor
clf;
plot(t, M(:,1), ";State 1;", "linewidth", 2, ...
t, M(:,2), ";State 2;", "linewidth", 2, ...
t, M(:,3), ";State 3;", "linewidth", 2, ...
t, M(:,4), ";State 4 (absorbing);", "linewidth", 2 );
legend("location","east"); legend("boxoff");
xlabel("Time");
ylabel("Time-averaged Expected sojourn time");
Produces the following figure
| Figure 1 |
|---|
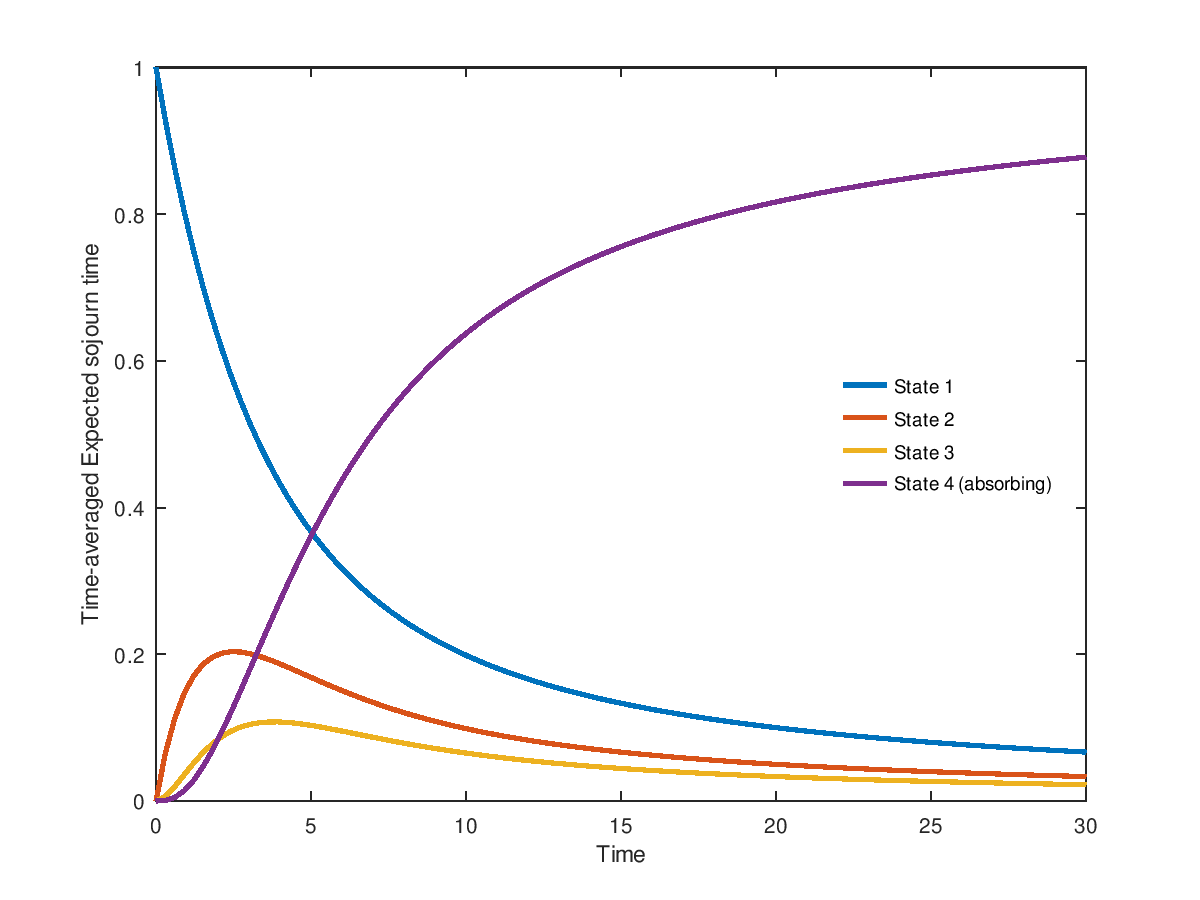 |
Demonstration 2
The following code
sec = 1;
min = sec*60;
hour = 60*min;
day = 24*hour;
# state space enumeration {2, RC, RB, 1, 0}
a = 1/(10*min); # 1/a = duration of reboot (10 min)
b = 1/(30*sec); # 1/b = reconfiguration time (30 sec)
g = 1/(5000*hour); # 1/g = processor MTTF (5000 hours)
d = 1/(4*hour); # 1/d = processor MTTR (4 hours)
c = 0.9; # coverage
Q = [ -2*g 2*c*g 2*(1-c)*g 0 0; ...
0 -b 0 b 0; ...
0 0 -a a 0; ...
d 0 0 -(g+d) g; ...
0 0 0 d -d];
p = ctmc(Q);
printf("System availability: %f\n",p(1)+p(4));
TT = linspace(0,1*day,101);
PP = ctmctaexps(Q,TT,[1 0 0 0 0]);
A = At = Abart = zeros(size(TT));
A(:) = p(1) + p(4); # steady-state availability
for n=1:length(TT)
t = TT(n);
p = ctmc(Q,t,[1 0 0 0 0]);
At(n) = p(1) + p(4); # instantaneous availability
Abart(n) = PP(n,1) + PP(n,4); # interval base availability
endfor
clf;
semilogy(TT,A,";Steady-state;", ...
TT,At,";Instantaneous;", ...
TT,Abart,";Interval base;");
ax = axis();
ax(3) = 1-1e-5;
axis(ax);
legend("boxoff");
Produces the following output
System availability: 0.999989
and the following figure
| Figure 1 |
|---|
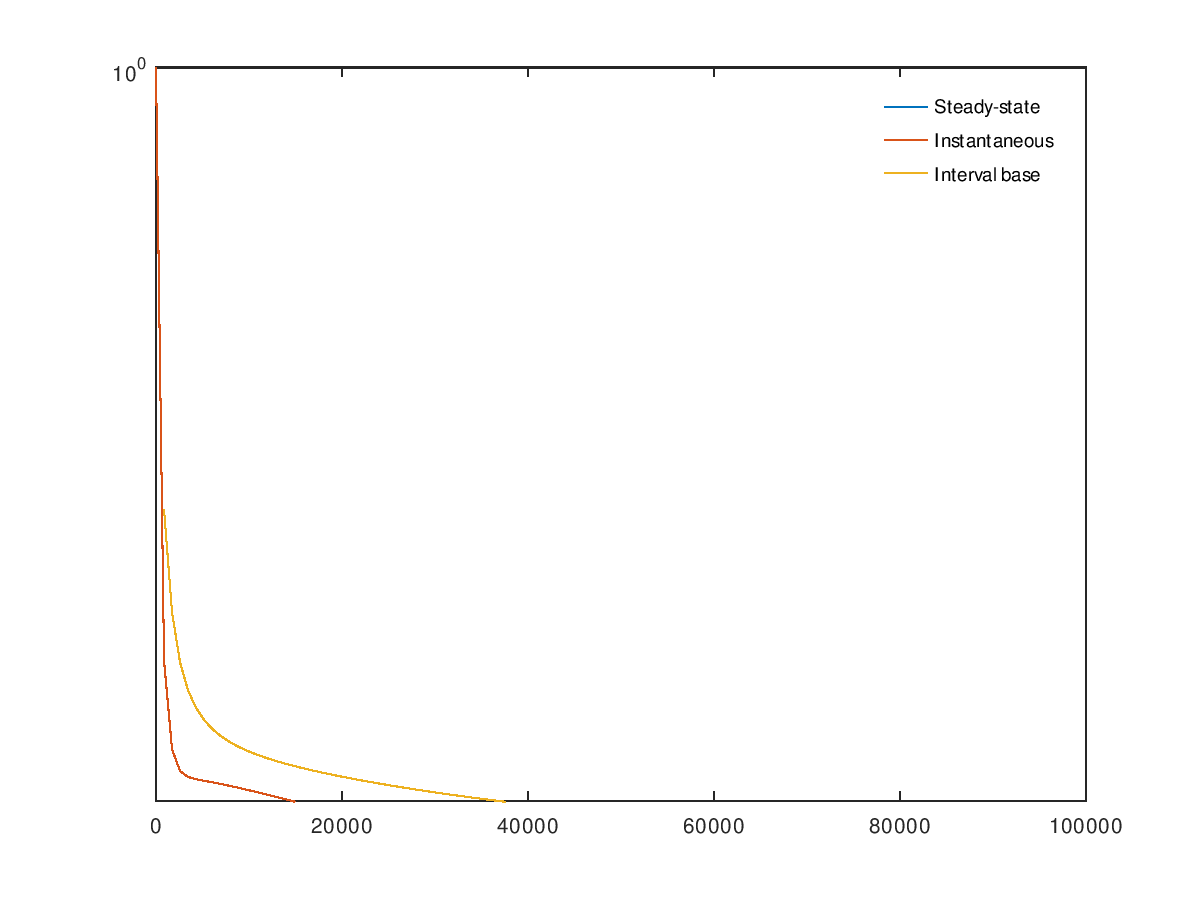 |
Package: queueing