- Function File: [U, R, Q, X, p0] = qsmminf (lambda, mu)
- Function File: pk = qsmminf (lambda, mu, k)
-
Compute utilization, response time, average number of requests and throughput for an infinite-server queue.
The M/M/\infty system has an infinite number of identical servers. Such a system is always stable (i.e., the mean queue length is always finite) for any arrival and service rates.
INPUTS
lambdaArrival rate (
lambda>0).muService rate (
mu>0).kNumber of requests in the system (
k ≥ 0).
OUTPUTS
UTraffic intensity (defined as \lambda/\mu). Note that this is different from the utilization, which in the case of M/M/\infty centers is always zero.
RService center response time.
QAverage number of requests in the system (which is equal to the traffic intensity \lambda/\mu).
XThroughput (which is always equal to
X = lambda).p0Steady-state probability that there are no requests in the system
pkSteady-state probability that there are k requests in the system (including the one being served).
If this function is called with less than three arguments, lambda and mu can be vectors of the same size. In this case, the results will be vectors as well.
REFERENCES
- G. Bolch, S. Greiner, H. de Meer and K. Trivedi, Queueing Networks and Markov Chains: Modeling and Performance Evaluation with Computer Science Applications, Wiley, 1998, Section 6.4
See also: qsmm1,qsmmm,qsmmmk.
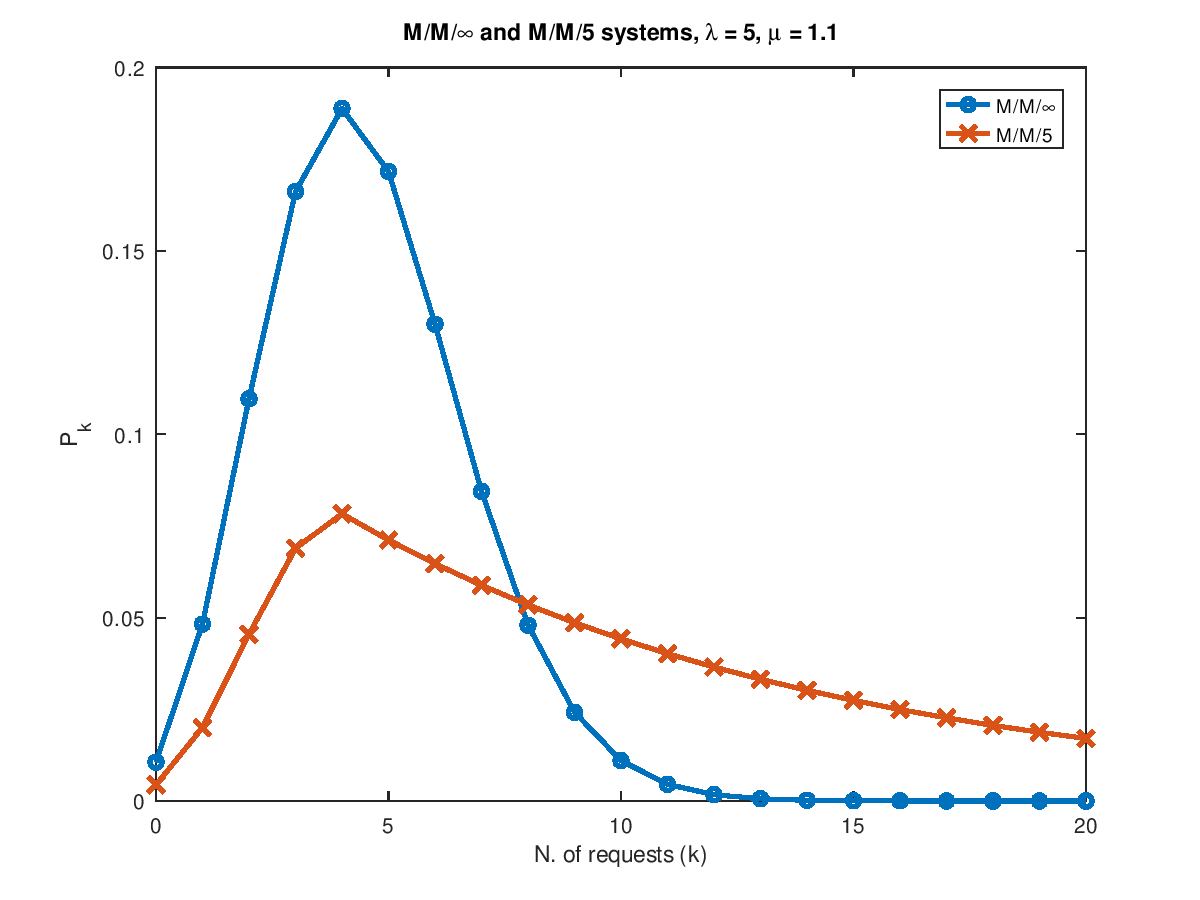
Demonstration 1
The following code
## Given a M/M/inf and M/M/m queue, compute the steady-state probability pk
## of having k requests in the systen.
lambda = 5;
mu = 1.1;
m = 5;
k = 0:20;
pk_inf = qsmminf(lambda, mu, k);
pk_m = qsmmm(lambda, mu, 5, k);
plot(k, pk_inf, "-o;M/M/\\infty;", "linewidth", 2, ...
k, pk_m, "-x;M/M/5;", "linewidth", 2);
xlabel("N. of requests (k)");
ylabel("P_k");
title(sprintf("M/M/\\infty and M/M/%d systems, \\lambda = %g, \\mu = %g", m, lambda, mu));
Produces the following figure
| Figure 1 |
|---|
 |
Package: queueing