- Function File: y = zmf (x, params)
- Function File: y = zmf ([x1 x2 ... xn], [a b])
-
For a given domain x and parameters params (or [a b]), return the corresponding y values for the Z-shaped membership function.
The argument x must be a real number or a non-empty vector of strictly increasing real numbers, and a and b must be real numbers, with a < b. This membership function satisfies:
1 if x <= a f(x) = 1 - 2 * ((x - a)/(b - a))^2 if a < x <= (a + b)/2 2 * ((x - b)/(b - a))^2 if (a + b)/2 < x < b 0 if x >= bwhich always returns values in the range [0, 1].
The parameters a and b specify:
- a == the rightmost point at which f(x) = 1
- b == the leftmost point at which f(x) = 0
At the midpoint of the segment [a, b], the function value is 0.5:
- f((a + b)/2) = 0.5
To run the demonstration code, type demo('zmf') at the Octave prompt.
See also: dsigmf, gauss2mf, gaussmf, gbellmf, pimf, psigmf, sigmf, smf, trapmf, trimf, zmf_demo.
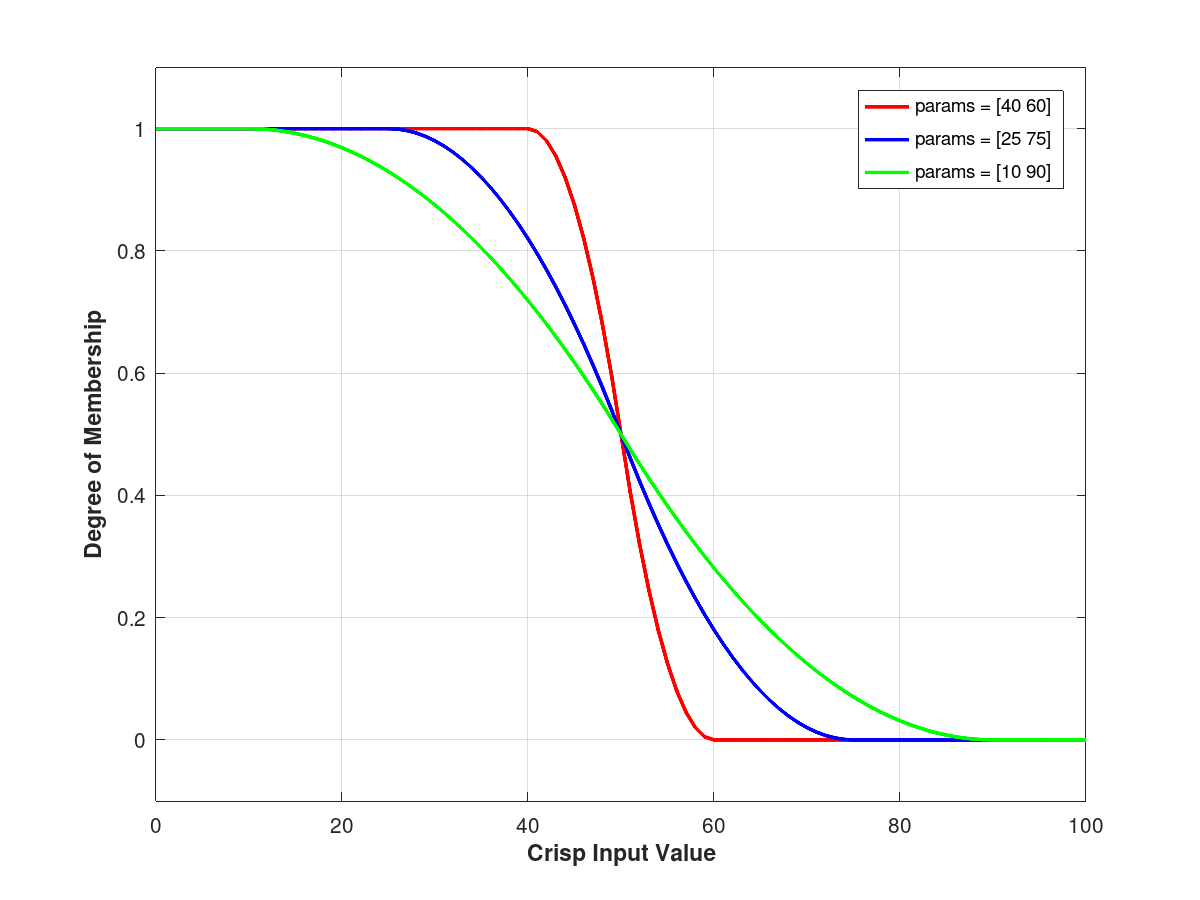
Demonstration 1
The following code
x = 0:100;
params = [40 60];
y1 = zmf(x, params);
params = [25 75];
y2 = zmf(x, params);
params = [10 90];
y3 = zmf(x, params);
figure('NumberTitle', 'off', 'Name', 'zmf demo');
plot(x, y1, 'r;params = [40 60];', 'LineWidth', 2)
hold on;
plot(x, y2, 'b;params = [25 75];', 'LineWidth', 2)
hold on;
plot(x, y3, 'g;params = [10 90];', 'LineWidth', 2)
ylim([-0.1 1.1]);
xlabel('Crisp Input Value', 'FontWeight', 'bold');
ylabel('Degree of Membership', 'FontWeight', 'bold');
grid;
Produces the following figure
| Figure 1 |
|---|
 |
Package: fuzzy-logic-toolkit