Function File: [tangent,inner] = beltProblem (c, r)

Finds the four lines tangent to two circles with given centers and radii.

The function solves the belt problem in 2D for circles with center c and radii r.

INPUT

c

2-by-2 matrix containig coordinates of the centers of the circles; one row per circle.

r

2-by-1 vector with the radii of the circles.

OUPUT

tangent

4-by-4 matrix with the points of tangency. Each row describes a segment(edge).

inner

4-by-2 vector with the point of intersection of the inner tangents (crossed belts) with the segment that joins the centers of the two circles. If the i-th edge is not an inner tangent then inner(i,:)=[NaN,NaN].

Example:

c         = [0 0;1 3];
r         = [1 0.5];
[T inner] = beltProblem(c,r)
⇒ T =
 -0.68516   0.72839   1.34258   2.63581
  0.98516   0.17161   0.50742   2.91419
  0.98675  -0.16225   1.49338   2.91888
 -0.88675   0.46225   0.55663   3.23112

⇒ inner =
  0.66667   2.00000
  0.66667   2.00000
      NaN       NaN
      NaN       NaN

See also: edges2d.

Demonstration 1

The following code

  c         = [0 0;1 3];
  r         = [1 0.5];
  [T inner] = beltProblem(c,r)

  figure(1)
  clf
  hold on
  h = drawEdge (T);
  set(h(find(~isnan(inner(:,1)))),'color','m');
  set(h,'linewidth',2);
  hold on
  drawCircle([c(1,:) r(1); c(2,:) r(2)],'linewidth',2);
  axis tight
  axis equal

 # -------------------------------------------------------------------
 # The circles with the tangents edges are plotted. The solution with
 # crossed belts (inner tangets) is shown in red.

Produces the following output

T =

  -0.68516   0.72839   1.34258   2.63581
   0.98516   0.17161   0.50742   2.91419
   0.98675  -0.16225   1.49338   2.91888
  -0.88675   0.46225   0.55663   3.23112

inner =

   0.66667   2.00000
   0.66667   2.00000
       NaN       NaN
       NaN       NaN

and the following figure

Figure 1

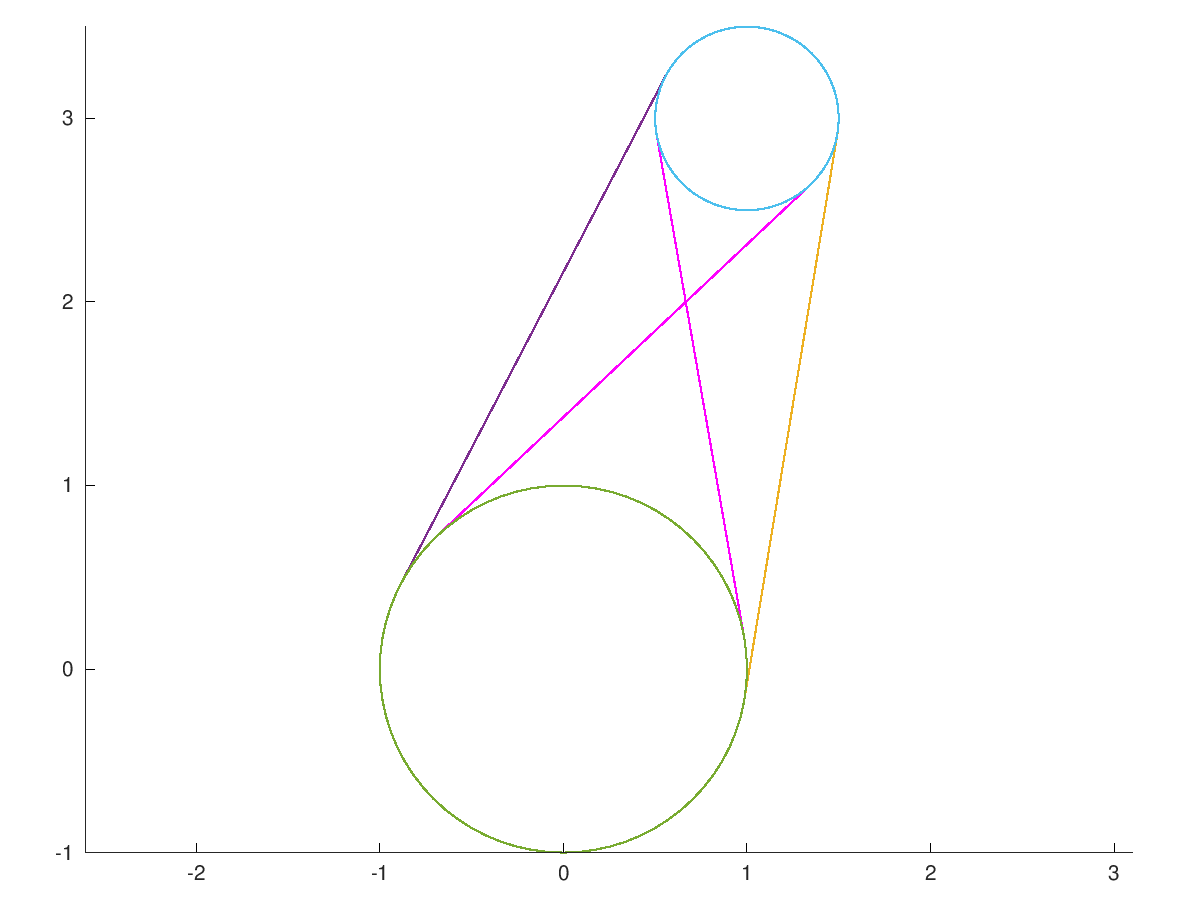Package: geometry