- Function File: cm = shapeCentroid (pp)
Centroid of a simple plane shape defined with piecewise smooth polynomials.
The shape is defined with piecewise smooth polynomials. pp is a cell where each elements is a 2-by-(poly_degree+1) matrix containing a pair of polynomials.
px(i,:) = pp{i}(1,:)andpy(i,:) = pp{i}(2,:).The edges of the shape should not self-intersect. This function does not check for the sanity of the shape.
See also: shapearea, shape2polygon.
Demonstration 1
The following code
# non-convex bezier shape
boomerang = {[ 0 -2 1; ...
-4 4 0]; ...
[0.25 -1; ...
0 0]; ...
[ 0 1.5 -0.75; ...
-3 3 0];
[0.25 0.75; ...
0 0]};
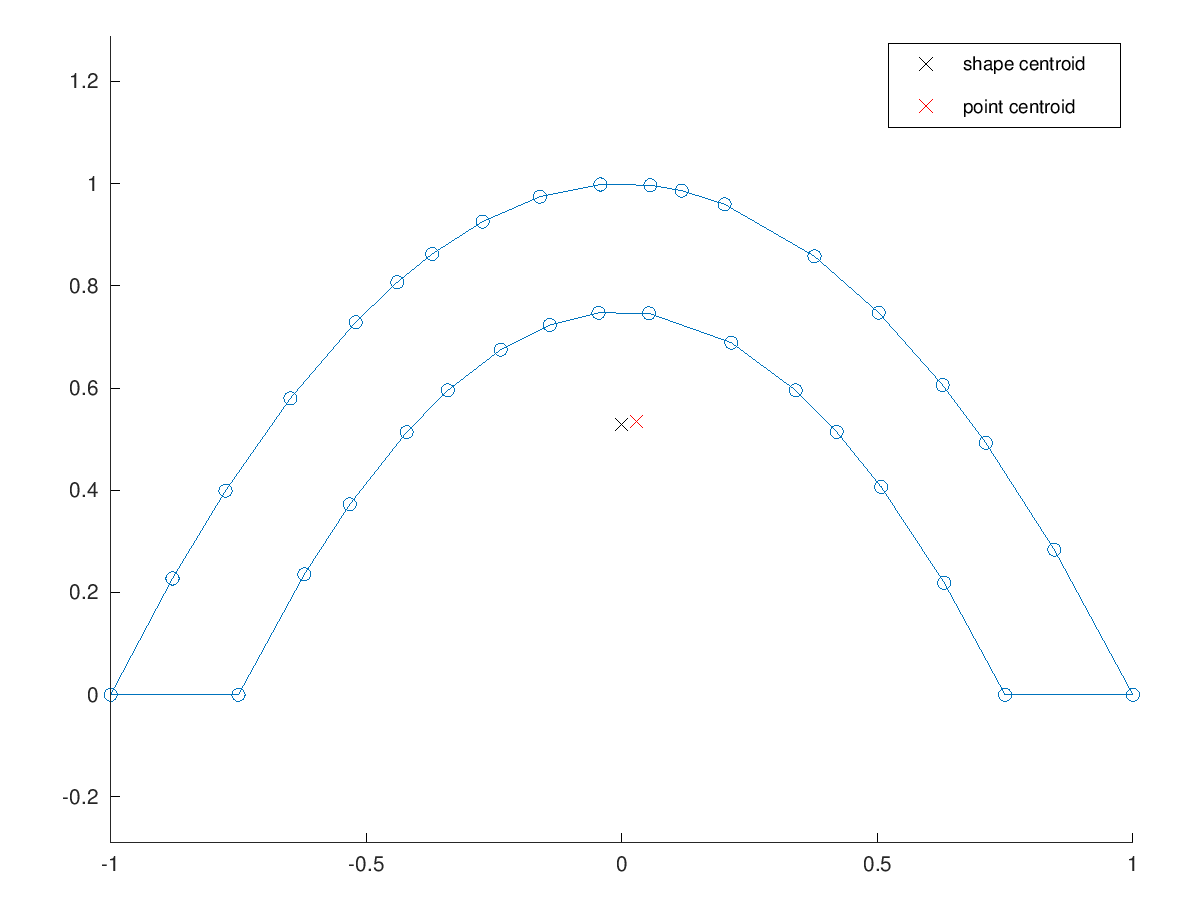
CoM = shapeCentroid (boomerang)
Gcentroid = centroid(shape2polygon(boomerang))
figure(1); clf;
plotShape(boomerang,'-o');
hold on
drawPoint(CoM,'xk;shape centroid;');
drawPoint(Gcentroid,'xr;point centroid;');
hold off
axis equal
Produces the following output
CoM = 0.00000 0.52857 Gcentroid = 0.029001 0.534364
and the following figure
| Figure 1 |
|---|
 |
Demonstration 2
The following code
Lshape = {[0.00000 0.76635; -0.67579 -0.24067]; ...
[0.77976 0.76635; 0.00000 -0.91646]; ...
[0.00000 1.54611; 0.38614 -0.91646]; ...
[-0.43813 1.54611; 0.00000 -0.53032]; ...
[0.00000 1.10798; 0.28965 -0.53032]; ...
[-0.34163 1.10798; 0.00000 -0.24067]};...
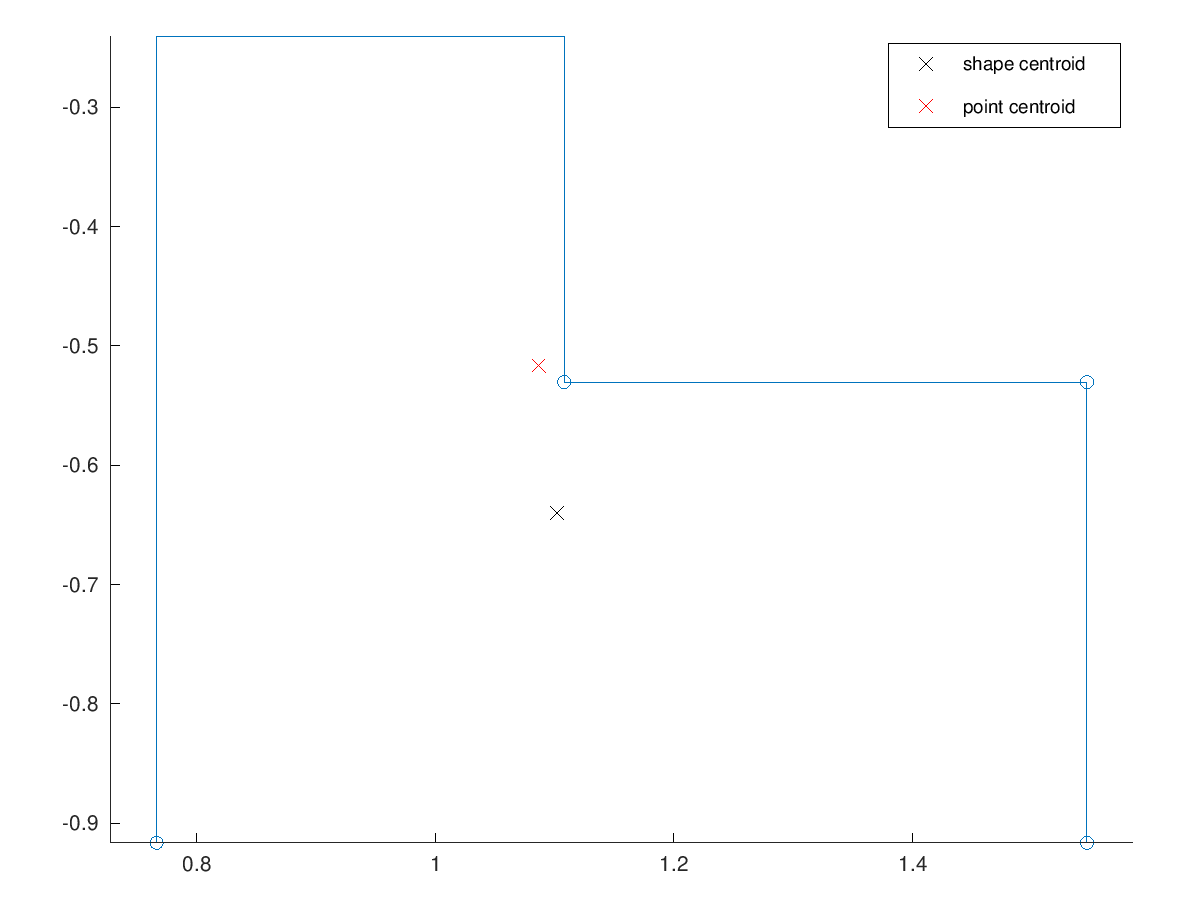
CoM = shapeCentroid (Lshape)
Gcentroid = centroid (shape2polygon (Lshape))
plotShape(Lshape,'-o');
hold on
drawPoint(CoM,'xk;shape centroid;');
drawPoint(Gcentroid,'xr;point centroid;');
hold off
axis equal
Produces the following output
CoM = 1.10204 -0.63981 Gcentroid = 1.08675 -0.51651
and the following figure
| Figure 1 |
|---|
 |
Package: geometry