- : [pline2 idx] = simplifyPolyline_geometry (pline)
- : … = simplifyPolyline_geometry (…,property,value,…)
Simplify or subsample a polyline using the Ramer-Douglas-Peucker algorithm, a.k.a. the iterative end-point fit algorithm or the split-and-merge algorithm.
The pline as a N-by-2 matrix. Rows correspond to the verices (compatible with
polygons2d). The vector idx constains the indexes on vetices in pline that generates pline2, i.e.pline2 = pline(idx,:).Parameters
- ‘'Nmax'’
Maximum number of vertices. Default value
1e3.- ‘'Tol'’
Tolerance for the error criteria. Default value
1e-4.- ‘'MaxIter'’
Maximum number of iterations. Default value
10.- ‘'Method'’
Not implemented.
Run
demo simplifyPolyline_geometryto see an example.See also: curve2polyline, curveval, simplifyPolygon_geometry.
Demonstration 1
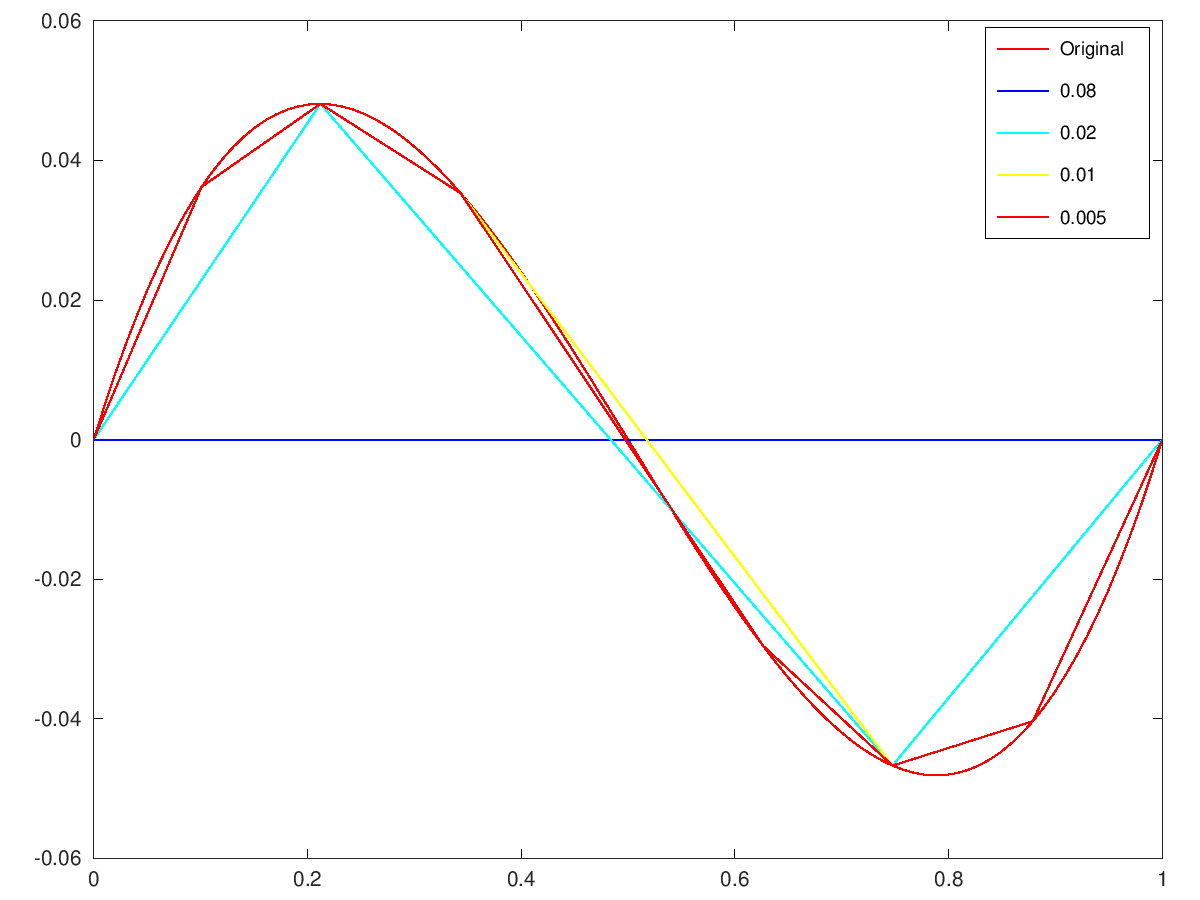
The following code
t = linspace(0,1,100).';
y = polyval([1 -1.5 0.5 0],t);
pline = [t y];
figure(1)
clf
plot (t,y,'-r;Original;','linewidth',2);
hold on
tol = [8 2 1 0.5]*1e-2;
colors = jet(4);
for i=1:4
pline_ = simplifyPolyline_geometry(pline,'tol',tol(i));
msg = sprintf('-;%g;',tol(i));
h = plot (pline_(:,1),pline_(:,2),msg);
set(h,'color',colors(i,:),'linewidth',2,'markersize',4);
end
hold off
# ---------------------------------------------------------
# Four approximations of the initial polyline with decreasing tolerances.
Produces the following figure
| Figure 1 |
|---|
 |
Demonstration 2
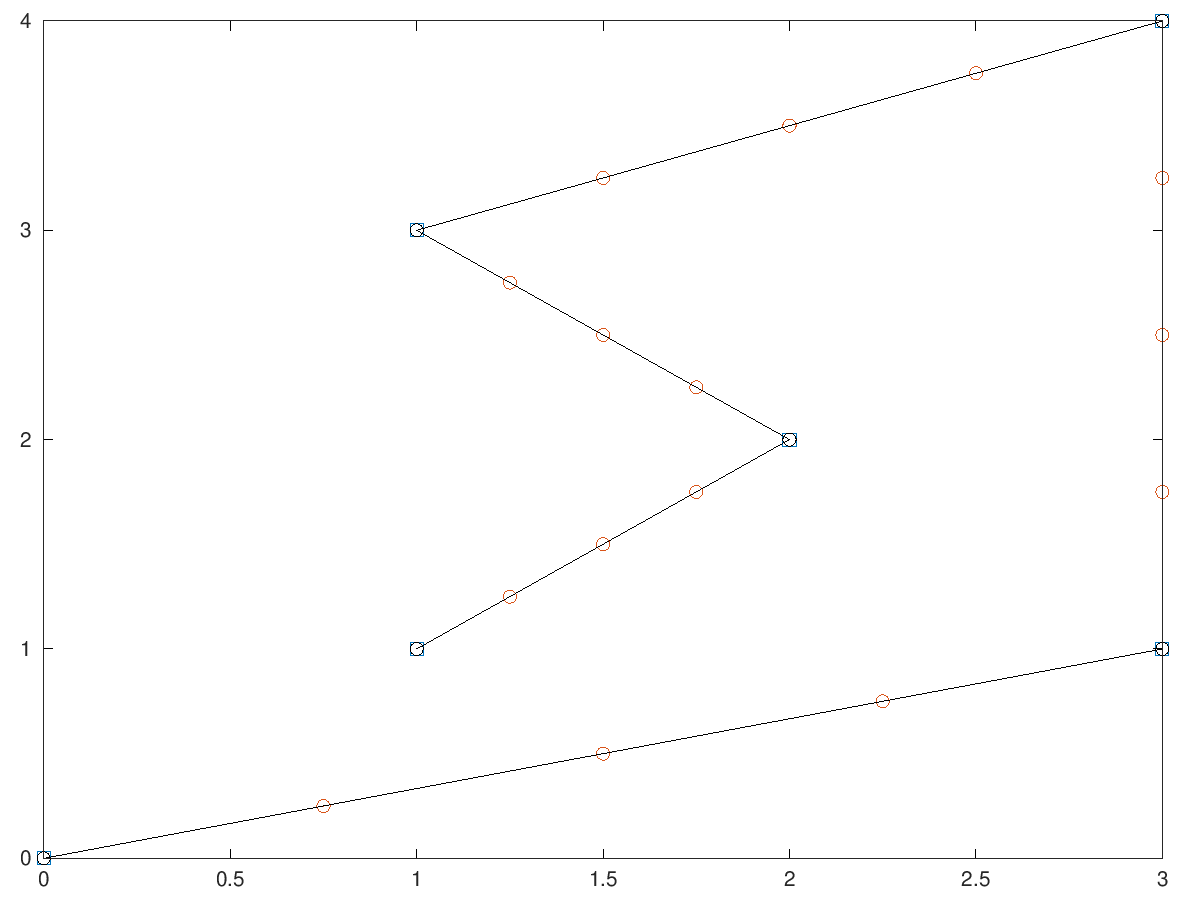
The following code
P = [0 0; 3 1; 3 4; 1 3; 2 2; 1 1];
func = @(x,y) linspace(x,y,5);
P2(:,1) = cell2mat( ...
arrayfun (func, P(1:end-1,1),P(2:end,1), ...
'uniformoutput',false))'(:);
P2(:,2) = cell2mat( ...
arrayfun (func, P(1:end-1,2),P(2:end,2), ...
'uniformoutput',false))'(:);
P2s = simplifyPolyline_geometry (P2);
plot(P(:,1),P(:,2),'s',P2(:,1),P2(:,2),'o',P2s(:,1),P2s(:,2),'-ok');
# ---------------------------------------------------------
# Simplification of a polyline in the plane.
Produces the following figure
| Figure 1 |
|---|
 |
Package: geometry