Function Reference: deconvwnr

: deconvwnr (I, PSF)

: deconvwnr (I, PSF, NSR)

Apply Wiener deconvolution filter.

The Wiener deconvolution algorithm estimates the original image from a deteriorated image I. It approximately undoes the filtering (e.g. blurring) that deteriorated the original image with a linear filter PSF ("point spread function") and additional additive noise. The amount of noise is specified by the parameter NSR ("noise to signal ratio"), also known as "regularisation parameter" K. This NSR parameter is meant as the ratio between the noise variance and the, unknown, original image variance. The resulting image is optimal in the sense that it minimises the mean square error to the original image.

The input image I can be of class uint8, uint16, int16, single, or double. The output image has the same class and size as I.

The filter PSF should be a float array. It can have any size that is smaller or equal to the size of I.

The noise parameter NSR must be non-negative and can either be given as a single float number, or as a float array (in Fourier domain) of the same size as I. It defaults to 0 (zero) which produces the, generally bad quality, direct inverse filtering.

See also: wiener2.

Demonstration 1

The following code

 I = phantom ();
 figure, imshow (I);
 title ("Original image");
 psf = fspecial ("motion", 30, 15);
 blurred = imfilter (I, psf, "conv");
 figure, imshow (blurred);
 title ("Image with added motion blur");
 var_noise = 0.00005;
 blurred_noisy = imnoise (blurred, "gaussian", 0, var_noise);
 figure, imshow (blurred_noisy);
 title ("Image with motion blur and added Gaussian noise");
 estimated_nsr = var_noise / (var(blurred_noisy(:)) - var_noise);
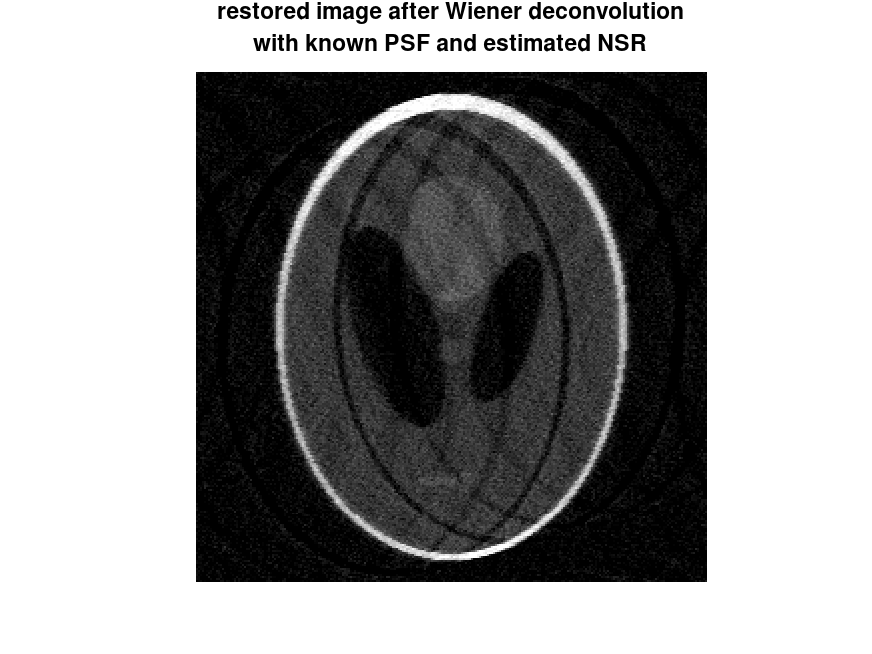
 J = deconvwnr (blurred_noisy, psf, estimated_nsr);
 figure, imshow (J)
 title ({"restored image after Wiener deconvolution",
           "with known PSF and estimated NSR"});

Produces the following figures

Figure 1	Figure 2	Figure 3	Figure 4

Package: image