- Function File: IM_OUT = imtransform (IM_IN, T) ¶
- Function File: IM_OUT = imtransform (IM_IN, T, interp) ¶
- Function File: IM_OUT = imtransform (…, prop, val) ¶
- Function File: [IM_OUT, xdata, ydata] = imtransform (…) ¶
Transform image.
Given an image IM_IN, return an image IM_OUT resulting from the forward transform defined in the transformation structure T. An additional input argument interp, ’bicubic’, ’bilinear’ (default) or ’nearest’, specifies the interpolation method to be used. Finally, the transform can be tuned using prop/val pairs. The following properties prop are supported:
- "udata"
Specifies the input space horizontal limits. val must be a two elements vector [minval maxval] in ascending order. Default: [1 columns(IM_IN)]
- "vdata"
Specifies the input space vertical limits. val must be a two elements vector [minval maxval] in ascending order. Default: [1 rows(IM_IN)]
- "xdata"
Specifies the required output space horizontal limits. val must be a two elements vector [first_col last_col] represents the coordinates of the first column and the last column of output image in the world coordinate system. Note: xdata can be in descending order, which causes a horizontal flip of the output image. Default: estimated using udata, vdata and findbounds function.
- "ydata"
Specifies the required output space vertical limits. val must be a two elements vector [first_row last_row] represents the coordinates of the first row and the last row of output image in the world coordinate system. Note: ydata can be in descending order, which cause a vertical flip of the output image. Default: estimated using udata, vdata and findbounds function.
- "xyscale"
Specifies the size of pixels in the output space. If a scalar is provided, both vertical and horizontal dimensions are scaled the same way. If val is a two element vector, it must indicate consecutively width and height of the output pixels. The default is to use the width and height of input pixels provided that it does not lead to a too large output image.
- "size"
Size of the output image (1-by-2 vector). Overrides the effect of "xyscale" property.
- "fillvalues"
Color of the areas where no interpolation is possible, e.g. when coordinates of points in the output space are out of the limits of the input space. val must be coherent with the input image format: for grayscale and indexed images (2D) val must be scalar, for RGB (n-by-m-by-3) val must be a 3 element vector.
The actual output limits, xdata and ydata vectors, are returned respectively as second and third output variables.
See also: maketform, cp2tform, tforminv, tformfwd, findbounds.
Demonstration 1
The following code
## Various linear transforms
figure ();
im = [checkerboard(20, 2, 4); checkerboard(40, 1, 2)];
%input space corners
incp = [1 1; 160 1; 160 160; 1 160];
udata = [min(incp(:,1)) max(incp(:,1))];
vdata = [min(incp(:,2)) max(incp(:,2))];
subplot (2,3,1);
imshow (im)
hold on
plot (incp(:,1), incp(:,2), 'ob')
axis on
xlabel ('Original')
% Translation and scaling
outcp = incp * 2;
outcp(:,1) += 200;
outcp(:,2) += 500;
T = maketform ('affine', incp(1:3,:), outcp(1:3,:));
subplot (2,3,2);
[im2 xdata ydata] = imtransform (im, T, 'udata', udata,
'vdata', vdata, 'fillvalues', 1);
imh = imshow (im2); set (imh, 'xdata', xdata, 'ydata', ydata)
set (gca, 'xlim', xdata, 'ylim', ydata)
axis on, hold on, xlabel ('Translation / Scaling');
plot (outcp(:,1), outcp(:,2), 'or')
% Shear
outcp = [1 1; 160 1; 140 160; -19 160]; % affine only needs 3 control points
T = maketform ('affine', incp(1:3,:), outcp(1:3,:));
subplot (2,3,3);
[im2 xdata ydata] = imtransform (im, T, 'udata', udata,
'vdata', vdata, 'fillvalues', 1);
imh = imshow (im2); set (imh, 'xdata', xdata, 'ydata', ydata)
set (gca, 'xlim', xdata, 'ylim', ydata)
axis on, hold on, xlabel ('Shear');
plot (outcp(:,1), outcp(:,2), 'or')
% Rotation
theta = pi/4;
T = maketform ('affine', [cos(theta) -sin(theta); ...
sin(theta) cos(theta); 0 0]);
outcp = tformfwd (T, incp);
subplot (2,3,4);
[im2 xdata ydata] = imtransform (im, T, 'udata', udata,
'vdata', vdata, 'fillvalues', 1 );
imh = imshow (im2); set (imh, 'xdata', xdata, 'ydata', ydata)
set (gca, 'xlim', xdata, 'ylim', ydata)
axis on, hold on, xlabel ('Rotation');
plot (outcp(:,1), outcp(:,2), 'or')
% Reflection around x axis
outcp = incp;
outcp(:,2) *= -1;
T = cp2tform (incp, outcp, 'similarity');
subplot (2,3,5);
[im2 xdata ydata] = imtransform (im, T, 'udata', udata,
'vdata', vdata, 'fillvalues', 1 );
imh = imshow (im2); set (imh, 'xdata', xdata, 'ydata', ydata)
set (gca, 'xlim', xdata, 'ylim', ydata)
axis on, hold on, xlabel ('Reflection');
plot (outcp(:,1), outcp(:,2), 'or')
% Projection
outcp = [1 1; 160 -40; 220 220; 12 140];
T = maketform ('projective', incp, outcp);
subplot (2,3,6);
[im2 xdata ydata] = imtransform (im, T, 'udata', udata,
'vdata', vdata, 'fillvalues', 1 );
imh = imshow (im2); set (imh, 'xdata', xdata, 'ydata', ydata)
set (gca, 'xlim', xdata, 'ylim', ydata)
axis on, hold on, xlabel ('Projection');
plot (outcp(:,1), outcp(:,2), 'or')
Produces the following figure
| Figure 1 |
|---|
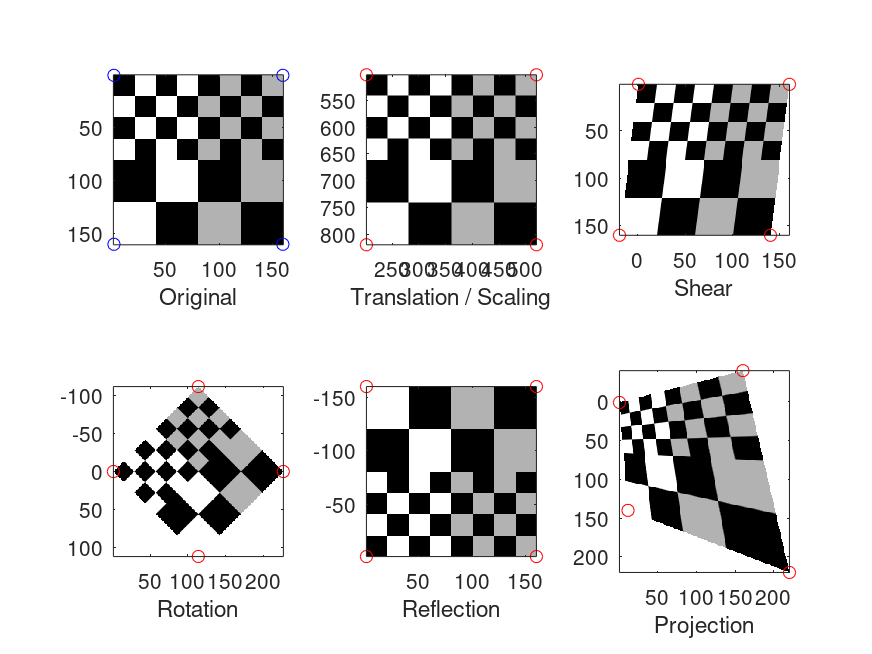 |
Demonstration 2
The following code
## Streched image
rad = 2; % minimum value: 4/pi
[uu vv] = meshgrid ((-2:2)/rad, (-2:2)/rad);
rescfactor = sin ((uu.^2 + vv.^2).^.5);
inpts = [(reshape (uu, numel (uu), 1)), (reshape (vv, numel (uu), 1))];
xx = rescfactor .* sign(uu);
yy = rescfactor .* sign(vv);
outpts = [reshape(xx, numel (xx), 1) reshape(yy, numel (yy), 1)];
T = cp2tform (inpts, outpts, "polynomial", 4);
figure;
subplot (1,2,1)
im = zeros (800, 800, 3);
im(:,:,1) = checkerboard (100) > 0.2;
im(:,:,3) = checkerboard (100) < 0.2;
[im2 xdata ydata] = imtransform (im, T, 'udata', [-2 2],
'vdata', [-2 2], 'fillvalues',
[0 1 0]);
imh = imshow (im2);
set (imh, 'xdata', xdata, 'ydata', ydata)
set (gca, 'xlim', xdata, 'ylim', ydata)
[im cmap] = imread ('default.img');
subplot (1,2,2)
[im2 xdata ydata] = imtransform (im, T, 'udata', [-1 1],
'vdata', [-1 1], 'fillvalues',
round (length (cmap) / 2));
imh = imshow (im2, cmap);
Produces the following figure
| Figure 1 |
|---|
 |
Package: image