- Method on
@infsup:X =fminsearch(f, X0)¶ - Method on
@infsup:[X, FVAL] =fminsearch(f, X0, options)¶ -
Minimize the function f over the interval box X0 and return rigorous bounds.
The function f may be multivariate, that is, the interval box X0 may be a vector, a matrix or an array of intervals. The output of the function must be scalar.
The rigorous bounds on FVAL satisfy 0 ≤ min {f (x) | x ∈ X0} - inf (FVAL) ≤ 1e-4 by default. Different accuracy requirements may be defined using options.TolFun.
[x, fval] = fminsearch (@cos, infsup ("[0, 4]")) ⇒ x ⊂ [3.114, 3.1858] fval ⊂ [-1, -0.99996]During each iteration the interval is bisected at its widest coordinate until the desired accuracy has been reached.
f = @(x) x(1) .^ 2 - x(2) .^ 2; [x, fval] = fminsearch (f, infsup ("[-1, 1] [-1, 1]")) ⇒ x ⊂ 1×2 interval vector [7.8828e-11, 8.8786e-06] [0.99991, 1] fval ⊂ [-1, -0.99991]Note that the algorithm tries to minimize FVAL and the returned value for X need not contain the minimum value of the function over X0; the value X is just “close” to one of possibly several places where the minimum occurs, that is, hull (f (X)) overlaps [M-ε, M+ε], where M is the actual minimum of the function f over X0 and ε equals options.TolFun. Also, it holds M ∈ FVAL, but in general it does not hold f (X) ⊆ FVAL.
It is possible to use the following optimization options: Display, MaxFunEvals, MaxIter, OutputFcn, TolFun, TolX.
f = @(x) -sin (hypot (x(1), x(2))) / hypot (x(1), x(2)); [x, fval] = fminsearch (f, infsup ("[-1, 1] [-1, 1]"), ... optimset ('MaxIter', 20)) ⇒ x ⊂ 1×2 interval vector [0, 1.9763e-323] [0, 1.9763e-323] fval ⊂ [-inf, -0.99999]The function utilizes the Skelboe-Moore algorithm and has been implemented after Algorithm 6.1 in R. E. Moore, R. B. Kearfott, and M. J. Cloud. 2009. Introduction to Interval Analysis. Society for Industrial and Applied Mathematics.
See also: optimset.
Demonstration 1
The following code
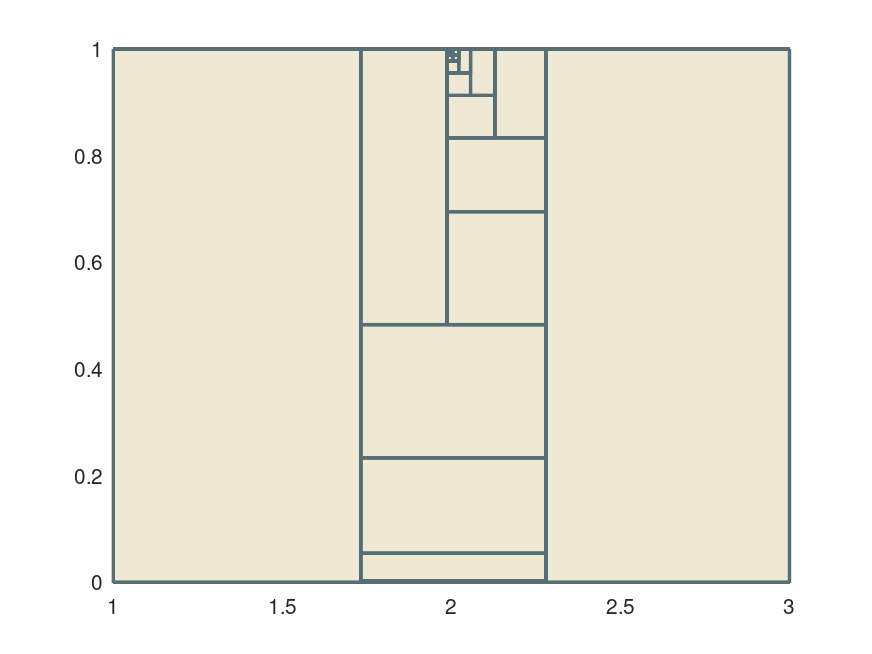
clf
hold on
draw = @(x) plot (x(1), x(2), [238 232 213]/255, [88 110 117]/255);
f = @(x) (x(1) - 2) .^ 2 - x(2) .^ 2;
fminsearch (f, infsup ("[1, 3] [0, 1]"), ...
optimset ('OutputFcn', draw));
hold off
Produces the following figure
| Figure 1 |
|---|
 |
Package: interval