4 Advanced Topics ¶
- Error Handling
- Decorations
- Specialized interval constructors
- Reverse Arithmetic Operations
- Tips and Tricks
- Validation
4.1 Error Handling ¶
Due to the nature of set-based interval arithmetic, one should not observe errors (in the sense of raised GNU Octave error messages) during computation unless operations are evaluated for incompatible data types. Arithmetic operations which are not defined for (parts of) their input, simply ignore anything that is outside of their domain.
However, the interval constructors can produce warnings depending on the input. The @infsup/infsup constructor will warn if the interval boundaries are invalid and returns empty intervals in these cases. Contrariwise, the (preferred) @infsupdec/infsupdec, midrad and hull constructors will only issue a warning and return [NaI] objects, which will propagate and survive through computations. NaI stands for “not an interval”.
Effects of set-based interval arithmetic on partial functions and the NaI object
## Evaluation of a function outside of its domain ## returns an empty interval infsupdec (2) / 0 ⇒ ans = [Empty]_trv infsupdec (0) ^ infsupdec (0) ⇒ ans = [Empty]_trv
## Illegal interval construction creates a NaI infsupdec (3, 2) -| warning: illegal interval boundaries: -| infimum greater than supremum ⇒ ans = [NaI]
## NaI even survives through computations ans + 1 ⇒ ans = [NaI]
There are some situations where the interval package cannot decide whether an error occurred or not and issues a warning. The user may choose to ignore these warnings or handle them as errors, see help warning for instructions.
- interval:PossiblyUndefined
- Reason
Interval construction with boundaries in decimal format, and the constructor can’t decide whether the lower boundary is smaller than the upper boundary. Both boundaries are very close and lie between subsequent binary64 numbers.
- Possible consequences
The constructed interval is a valid and tight enclosure of both numbers. If the lower boundary was actually greater than the upper boundary, this illegal interval is not considered an error.
- interval:ImplicitPromote
- Reason
An interval operation has been evaluated on both, a bare and a decorated interval. The bare interval has been converted into a decorated interval in order to produce a decorated result. Note: This warning does not occur if a bare interval literal string gets promoted into a decorated interval, e. g.,
infsupdec (1, 2) + "[3, 4]"does not produce this warning whereasinfsupdec (1, 2) + infsup (3, 4)does. A bare interval can be explicitly promoted with the @infsup/newdec function.- Possible consequences
The implicit conversion applies the best possible decoration for the bare interval. If the bare interval has been produced from an interval arithmetic computation, this branch of computation is not covered by the decoration information and the final decoration could be considered wrong. For example,
infsupdec (1, 2) + infsup (0, 1) ^ 0would ignore that 0^0 is undefined.
- interval:UndefinedOperation
- Reason
An error has occurred during interval construction and the NaI object has been produced (an empty interval in case of the bare interval constructor). The warning text contains further details. A NaI can be explicitly created with the nai function.
- Possible consequences
Nothing bad is going to happen, because the semantics of NaI and empty intervals are well defined by IEEE Std 1788-2015. However, the user might choose to cancel the algorithm immediately when the NaI is encountered for the first time.
Table 4.1: Warning IDs
4.2 Decorations ¶
The interval package provides a powerful decoration system for intervals, as specified by IEEE Std 1788-2015, IEEE standard for interval arithmetic. By default any interval carries a decoration, which collects additional information about the course of function evaluation on the interval data.
Only the (unfavored) @infsup/infsup constructor creates bare, undecorated intervals and the @infsupdec/intervalpart operation may be used to demote decorated intervals into bare, undecorated ones. It is highly recommended to always use the decorated interval arithmetic, which gives additional information about an interval result in exchange for a tiny overhead.
The following decorations are available:
| Decoration | Bounded | Continuous | Defined | Definition |
|---|---|---|---|---|
| com (common) | ✓ | ✓ | ✓ | x is a bounded, nonempty subset of Dom(f); f is continuous at each point of x; and the computed interval f(x) is bounded |
| dac (defined and continuous) | ✓ | ✓ | x is a nonempty subset of Dom(f); and the restriction of f to x is continuous | |
| def (defined) | ✓ | x is a nonempty subset of Dom(f) | ||
| trv (trivial) | always true (so gives no information) | |||
| ill (ill-formed) | Not an interval, at least one interval constructor failed during the course of computation |
The decoration information is especially useful after a very long and complicated function evaluation. For example, when the “def” decoration survives until the final result, it is proven that the overall function is actually defined for all values covered by the input intervals.
Examples of using the decoration system
x = infsupdec (3, 4) ⇒ x = [3, 4]_com y = x - 3.5 ⇒ y = [-0.5, +0.5]_com
## The square root function ignores any negative part of the input, ## but the decoration indicates whether this has or has not happened. sqrt (x) ⇒ ans ⊂ [1.732, 2]_com sqrt (y) ⇒ ans ⊂ [0, 0.70711]_trv
Please note that decoration information will not survive through reverse operations (see below) and set operations.
4.3 Specialized interval constructors ¶
Above mentioned interval construction with decimal numbers or numeric data is straightforward. Beyond that, there are more ways to define intervals or interval boundaries.
- Hexadecimal-floating-constant form: Each interval boundary may be defined by a hexadecimal number (optionally containing a point) and an exponent field with an integral power of two as defined by the C99 standard ISO/IEC9899, N1256, §6.4.4.2. This can be used as a convenient way to define interval boundaries in binary64 precision, because the hexadecimal form is much shorter than the decimal representation of many numbers.
- Rational literals: Each interval boundary may be defined as a fraction of two decimal numbers. This is especially useful if interval boundaries shall be tightest enclosures of fractions, that would be hard to write down as a decimal number.
- Uncertain form: The interval as a whole can be defined by a midpoint or upper/lower boundary and an integral number of “units in last place” (ULPs) as an uncertainty. The format is
m?ruE, wheremis a mantissa in decimal,
ris either empty (which means ½ ULP) or is a non-negative decimal integral ULP count or is the ? character (for unbounded intervals),
uis either empty (symmetrical uncertainty of r ULPs in both directions) or is either u (up) or d (down),
Eis either empty or an exponent field comprising the character
efollowed by a decimal integer exponent (base 10).
Examples of different formats during interval construction
infsupdec ("0x1.999999999999Ap-4") # hex-form
⇒ ans ⊂ [0.1, 0.10001]_com
infsupdec ("1/3", "7/9") # rational form
⇒ ans ⊂ [0.33333, 0.77778]_com
infsupdec ("121.2?") # uncertain form
⇒ ans ⊂ [121.14, 121.25]_com
infsupdec ("5?32e2") # uncertain form with ulp count
⇒ ans = [-2700, +3700]_com
infsupdec ("-42??u") # unbound uncertain form
⇒ ans = [-42, +inf]_dac
The hex-form can be set for output with the format hex command.
4.4 Reverse Arithmetic Operations ¶
Some arithmetic functions also provide reverse mode operations. That is inverse functions with interval constraints. For example the @infsup/sqrrev function can compute the inverse of the x .^ 2 function on intervals. The syntax is sqrrev (C, X) and will compute the enclosure of all numbers x ∈ X that fulfill the constraint x² ∈ C.
In the following example, we compute the constraints for base and exponent of the power function pow as shown in the figure.
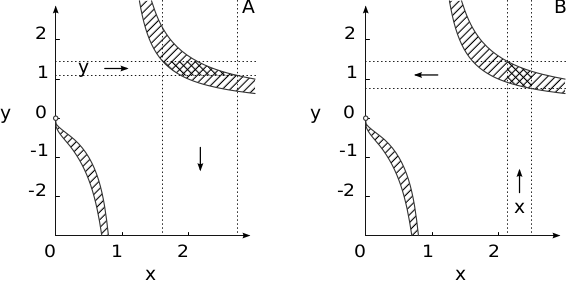
Figure 4.1: Reverse power operations. A relevant subset of the function’s domain is outlined and hatched. In this example we use x^y ∈ [2, 3].
x = powrev1 (infsupdec ("[1.1, 1.45]"), infsupdec (2, 3))
⇒ x ⊂ [1.6128, 2.7149]_trv
y = powrev2 (infsupdec ("[2.14, 2.5]"), infsupdec (2, 3))
⇒ y ⊂ [0.75647, 1.4441]_trv
4.5 Tips and Tricks ¶
For convenience it is possible to implicitly call the interval constructor during all interval operations if at least one input already is an interval object.
infsupdec ("17.7") + 1
⇒ ans ⊂ [18.699, 18.701]_com
ans + "[0, 2]"
⇒ ans ⊂ [18.699, 20.701]_com
Interval functions with only one argument can be called by using property syntax, e. g. x.inf, x.sup or even x.sqrt.
Whilst most functions (@infsup/size, @infsup/isvector, @infsup/ismatrix, …) work as expected on interval data types, the function @infsup/isempty is evaluated element-wise and checks if an interval equals the empty set.
builtin ("isempty", empty ())
⇒ ans = 0
isempty (empty ())
⇒ ans = 1
4.6 Validation ¶
The interval package contains an extensive test suite, which can be run with the command __run_test_suite__ ({pkg("list", "interval"){}.dir}, {}) to verify correct functionality for a particular system.
In addition, examples from the package documentation can be verified using the doctest package:
pkg load doctest
doctest (pkg ("list", "interval"){}.dir)