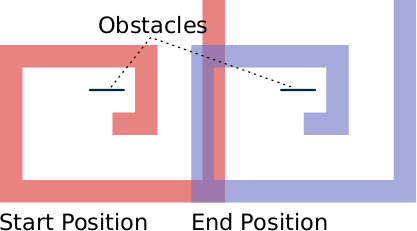
Figure 3.1: Cameleon Problem: The polygon has to be moved from the left to the right without touching any obstacles along the path.
Previous: Parameter Estimation, Up: Examples [Contents]

Figure 3.1: Cameleon Problem: The polygon has to be moved from the left to the right without touching any obstacles along the path.
The problem presented here is a simplified version from the paper L. Jaulin (2001). Path planning using intervals and graphs. Reliable Computing, issue 1, volume 7, 1–15.
There is an object, a simple polygon in this case, which shall be moved from a starting position to a specified target position. Along the way there are obstacles which may not be touched by the polygon. The polygon can be moved in one direction (left to right or right to left) and may be rotated around its lower left corner.
This makes a two dimensional parameter space and any feasible positions can be determined using interval arithmetic like in the examples above.
Then we use a simple path planning algorithm: We move along the centers of adjacent and feasible boxes in the parameter space until we have a closed path from the start position to the end position. The path is guaranteed to be feasible, that is, there will be no collisions if we follow the path.
# We can build the simple polygon from interval boxes
global polygon_x = ...
infsup ("[18,20] [0,20] [0, 2] [ 0,14] [12,14] [10,14]")';
global polygon_y = ...
infsup ("[ 0,18] [0, 2] [0,14] [12,14] [ 6,14] [ 6, 8]")';
global obstacle_x = infsup ("[ 8,11] [25,28]");
global obstacle_y = infsup ("[10,10] [10,10]");
color_feasible = [238 232 213] ./ 255;
color_uncertain = [220 50 47] ./ 255;
color_path = [133 153 0] ./ 255;
function feasible = check_collision (obstacle_x, obstacle_y)
global polygon_x;
global polygon_y;
feasible = infsup (zeros (size (obstacle_x)), ...
ones (size (obstacle_x)));
# Check if the obstacle is inside the polygon
inside = any (...
subset (obstacle_x, polygon_x) & subset (obstacle_y, polygon_y));
feasible(inside) = 0;
# Check if the obstacle is outside the polygon
outside = all (...
disjoint (obstacle_x, polygon_x) | ...
disjoint (obstacle_y, polygon_y));
feasible(outside) = 1;
endfunction
function feasible = check_parameters (x_offset, angle)
global obstacle_x;
global obstacle_y;
# Instead of rotating the polygon, we rotate the obstacles (reverse)
s = sin (-angle);
c = cos (-angle);
f_x = @(x, y) (x - x_offset) .* c - y .* s;
f_y = @(x, y) (x - x_offset) .* s + y .* c;
# All obstacles must be considered
feasible = 1;
for i = 1 : numel (obstacle_x)
feasible = min (feasible, ...
check_collision (f_x (obstacle_x(i), obstacle_y(i)), ...
f_y (obstacle_x(i), obstacle_y(i))));
endfor
endfunction
# Compute a paving of feasible polygon states
[x, paving, inner] = fsolve (...
@check_parameters, ...
infsup ("[-28, 57] [-1.4, 2.7]"), ...
1, ...
struct ('MaxIter', 21, 'TolX', 0.03));
hold on
plot (paving(1, inner), paving(2, inner), color_feasible);
plot (paving(1, not (inner)), paving(2, not (inner)), color_uncertain);
# Consider only states that are guaranteed to be feasible
paving = paving (:, inner);
# Path search
start_idx = find (all (ismember ([0; 0], paving)), 1);
end_idx = find (all (ismember ([17; 0], paving)), 1);
adjacency = not (disjoint (paving(1, :), transpose (paving(1, :))) | ...
disjoint (paving(2, :), transpose (paving(2, :))));
# Do a Dijkstra search until we reach end_idx
distance = inf (columns (paving), 1); # nan = visited
previous = zeros (columns (paving), 1);
distance(start_idx) = 0;
while (not (isnan (distance(end_idx))))
[pivot_distance, pivot_idx] = min (distance);
visited = isnan (distance);
neighbors_idx = adjacency(:, pivot_idx) & not (visited);
if (not (any (neighbors_idx)))
error ("Cannot reach target location")
endif
neighbors_distance = subsasgn (...
distance, ...
substruct ("()", {neighbors_idx}), ...
pivot_distance + hypot (...
# Compute distance between centers of boxes
mid (paving(1, pivot_idx)) - mid (paving(1, neighbors_idx)), ...
mid (paving(2, pivot_idx)) - mid (paving(2, neighbors_idx))));
shorter_path = neighbors_idx & (neighbors_distance < distance);
previous(shorter_path) = pivot_idx;
distance(shorter_path) = neighbors_distance(shorter_path);
distance(pivot_idx) = nan;
endwhile
# Plot the path to the target location last_idx = end_idx; while (last_idx != start_idx) next_idx = previous(last_idx); x1 = mid (paving(1, last_idx)); y1 = mid (paving(2, last_idx)); x2 = mid (paving(1, next_idx)); y2 = mid (paving(2, next_idx)); plot ([x1 x2], [y1 y2], 'linewidth', 2, 'color', color_path); last_idx = next_idx; endwhile
The script visualizes the solution in the parameter space. Unfeasible parameters are white, and uncertain combinations of parameters are red. The algorithm’s accuracy is just good enough to find a closed path, which is drawn in green color. The uncertain red area is quite big because we have used a very simple check for verification whether the polygon overlaps the obstacles. This could be improved.
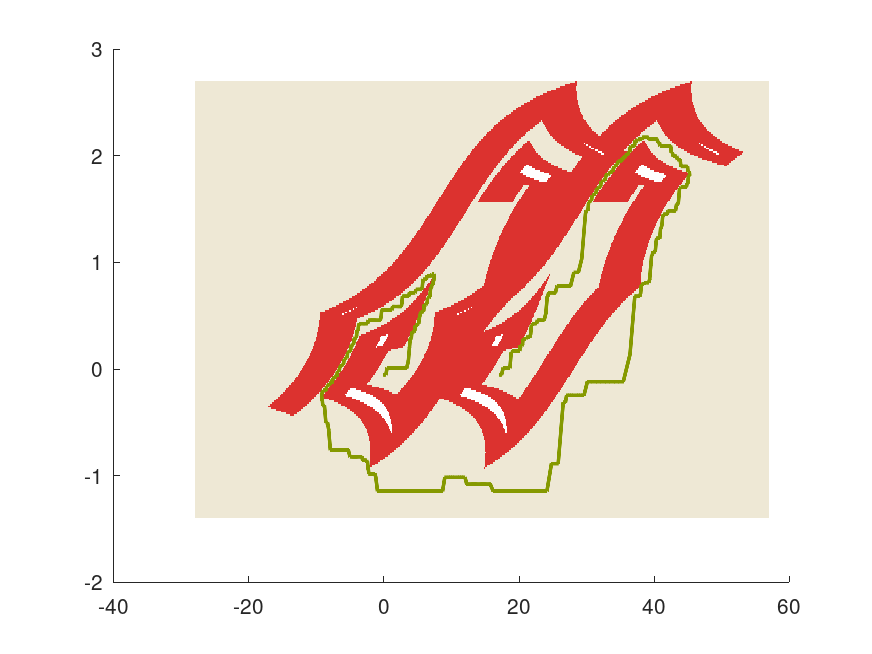
The solution is not optimal, please refer to Luc Jaulin’s paper for more sophisticated approaches. However, we could find a valid solution that moves the polygon as desired without touching any obstacles.
Figure 3.2: Cameleon Problem: A possible solution which moves the polygon from the left to the right without touching obstacles.
Previous: Parameter Estimation, Up: Examples [Contents]