Navigation

Operators and Keywords

Function List:

C++ API

Function File: irsa_jitsp.m

jitxp = irsa_jitsp (Tm, jit, N [, rfunc])

Generate N sampling points with a minimum distance Tm and an additional random distance jit with random distribution rfunc

Input:

Tm : Scalar – mean sampling period

N : Scalar – number of sampling points to generate

jit : Scalar – factor in [0,1] describing the part of Tm which is jittered.

rfunc: String (i.e. in quotes) of a random distribution function. Has to take the number of rows as the first and the number of columns as the second argument. Default is 'rand'.

rmin : Scalar – Lower limit of random distribution function computed with rfunc

rmax : Scalar – Upper limit of random distribution function

Output:

jitxp : Columnvector – sampling points with a jitter

Note:

1) The first sampling point will be 0, the last (N-1)*Tm. No jitter is added to them.

2) If you use a random distribution function and dont give a upper or lower limit it's assumed to be limited by its present computed maximum or minimum values.

Demonstration 1

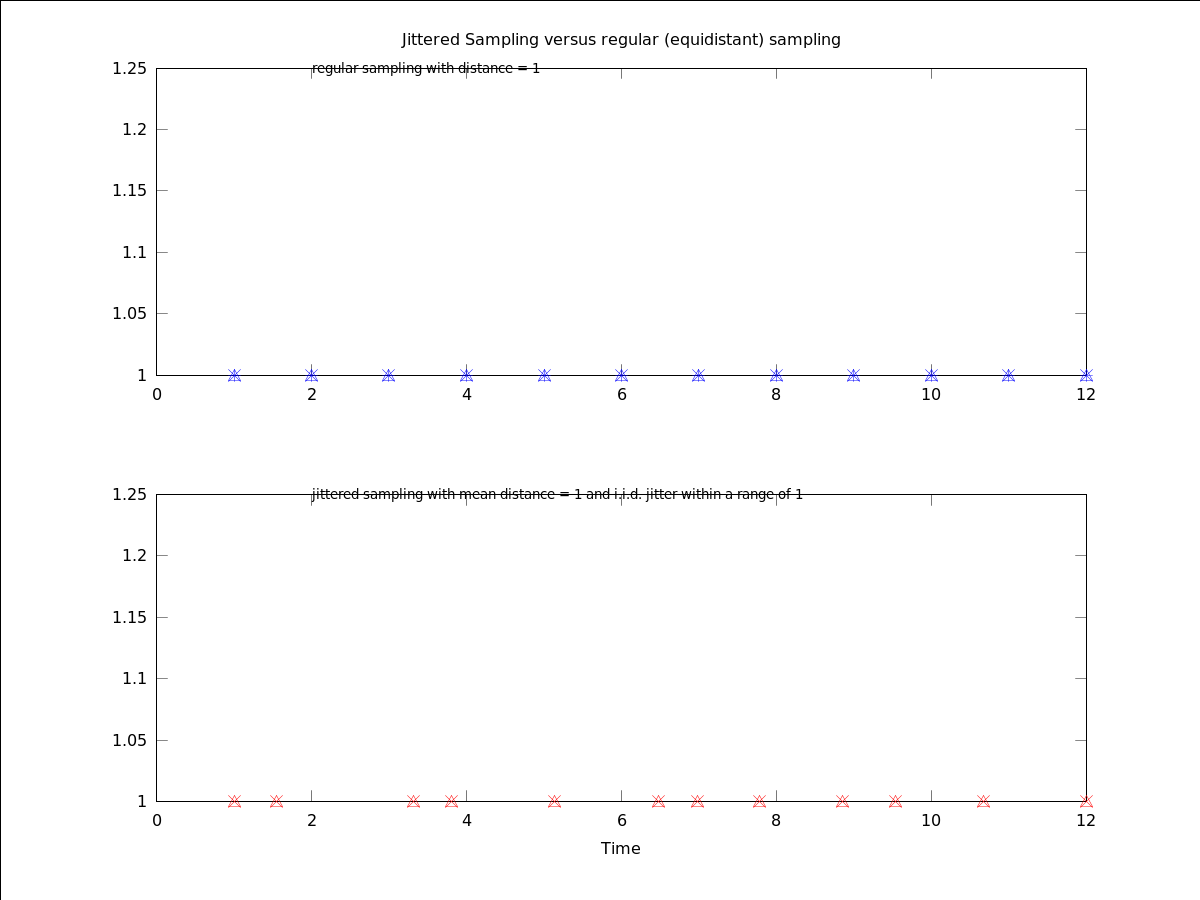
The following code

 N = 12;
 eqxp = irsa_jitsp( 1 , N, 0 ) + 1;
 jitxp = irsa_jitsp( 1 , N, 1 ) + 1;
 o = ones(N,1);
 ## Plot 
 figure();
 legend('off');
 axis([0,13,0,1.5]);
 subplot( 211 );
 plot( eqxp, o, '^b', eqxp, o, '*b' ); text(); title("");
 title( "Jittered Sampling versus regular (equidistant) sampling" );
 text( 2,1.25, 'regular sampling with distance = 1' );
 subplot( 212 );
 plot( jitxp, o, '^r', jitxp, o, 'xr' ); text; 
 xlabel( "Time" );
 text( 2,1.25, 'jittered sampling with mean distance = 1 and i.i.d. jitter within a range of 1' );

Produces the following figure

Figure 1