Navigation

Operators and Keywords

Function List:

C++ API

Function File: [mesh, vmap] = ls_build_mesh (geom, phi, glob = false)

Build a triangle mesh for the level-set geometry described by geom and by the level-set function phi. Note that geom must contain absolute coordinates as set by ls_absolute_geom.

If glob is set to true, then the mesh will contain the whole hold-all domain and not just the interior of the level-set geometry. It will, however, be constructed such that the boundary of the level-set domain is resolved precisely, and such that the level-set domain can be described as a subset of the mesh triangles.

The mesh points will be made up both of grid nodes as well as intersection points. While all intersection points will appear as mesh nodes, unless glob is set, only inner grid nodes will correspond to mesh points. The points on the mesh are numbered differently to the points in geom, although the indices can be translated both ways using vmap (see below).

On the other hand, the boundary edges of the mesh match precisely the edges given in geom.bedges. They have the same indices in both data structures.

The returned struct mesh follows the format of the msh package, which means that it contains these fields:

p

2 x np matrix which contains the x- and y-coordinates of the mesh points in its two rows.

t

4 x nt matrix describing the mesh triangles. The first three rows contain the indices of mesh points making up the triangle, and the fourth row contains the index of the geometrical surface this triangle belongs to. It is always set to 1 for now. The points are ordered counter-clockwise (in the coordinate-system interpretation of the grid).

e

7 x ne matrix describing the edges of the mesh. They correspond precisely to geom.bedges. The rows of this matrix are:

1–2

Start- and end-point index. They are ordered such that the level-set domain is on the left of the edge.

3–4

Always 0 for compatibility.

5

The gamma component index (as per geom.gamma) that contains this edge. Will be in the range 1–geom.gamma.n.

6–7

Geometrical surface index of the domain parts to the right and left. They are set to 0 and 1 for now.

The second output, vmap, describes the mappings between geometrical node / intersection-point indices in geom and the indices of the mesh points used in mesh. It is a struct with these fields:

grid

Maps the index of a node on the grid to the index of the corresponding mesh point. The value is NA if the mesh does not contain the point.

ispt

Maps the index of an intersection point (according to geom.ispts) to the index of the corresponding mesh point.

mesh

Maps the index of a mesh point back to either the grid or intersection-point index. A positive value means that the mesh point is on the grid and has the respective index, while a negative value means that it is an intersection point with index equal to the absolute value of the entry.

See also: ls_find_geometry, ls_absolute_geom, msh2m_structured_mesh.

Demonstration 1

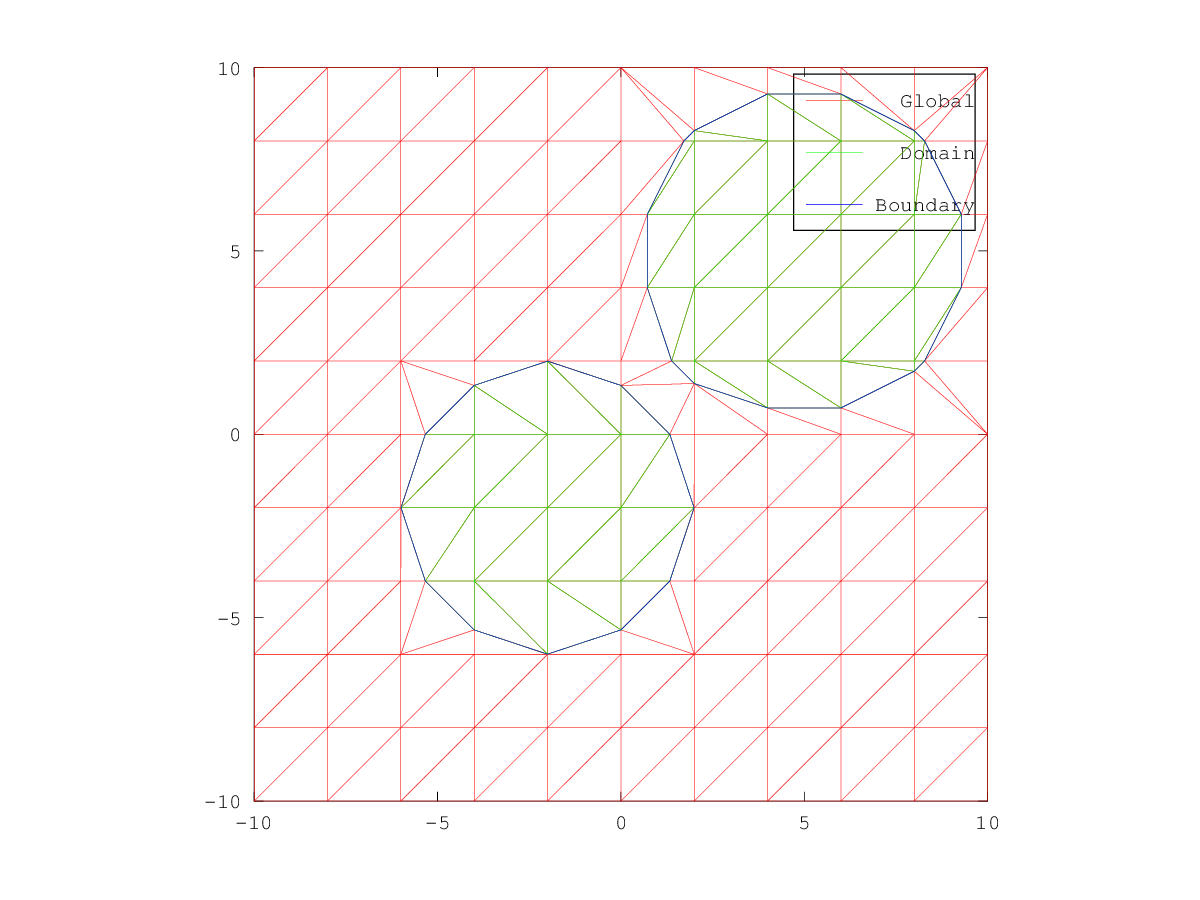
The following code

  x = linspace (-10, 10, 11);
  h = x(2) - x(1);
  [XX, YY] = meshgrid (x, x);

  phi = ls_union (ls_genbasic (XX, YY, "sphere", [5, 5], 4.5), ...
                  ls_genbasic (XX, YY, "sphere", [-2, -2], 4));
  phi = ls_normalise (phi, h);
  geom = ls_find_geometry (phi, h);
  geom = ls_absolute_geom (geom, XX, YY);

  mesh = ls_build_mesh (geom, phi, false);
  meshGlob = ls_build_mesh (geom, phi, true);

  figure ();
  hold ("on");
  trimesh (meshGlob.t(1 : 3, :)', meshGlob.p(1, :), meshGlob.p(2, :), "r");
  trimesh (mesh.t(1 : 3, :)', mesh.p(1, :), mesh.p(2, :), "g");
  for i = 1 : size (mesh.e, 2)
    plot (mesh.p(1, mesh.e(1 : 2, i)), mesh.p(2, mesh.e(1 : 2, i)), "b");
  endfor
  hold ("off");
  legend ("Global", "Domain", "Boundary");
  axis ("equal");
  axis ("square");

Produces the following figure

Figure 1

Package: level-set