- Function File: [W, H] = nmf_pg (V, Winit, Hinit, tol, timelimit, maxiter)
-
Non-negative matrix factorization by alternative non-negative least squares using projected gradients.
The matrix V is factorized into two possitive matrices W and H such that
V = W*H + U. Where U is a matrix of residuals that can be negative or positive. When the matrix V is positive the order of the elements in U is bounded by the optional named argument tol (default value1e-9).The factorization is not unique and depends on the inital guess for the matrices W and H. You can pass this initalizations using the optional named arguments Winit and Hinit.
timelimit, maxiter: limit of time and iterations
Examples:
A = rand(10,5); [W H] = nmf_pg(A,tol=1e-3); U = W*H -A; disp(max(abs(U)));
Demonstration 1
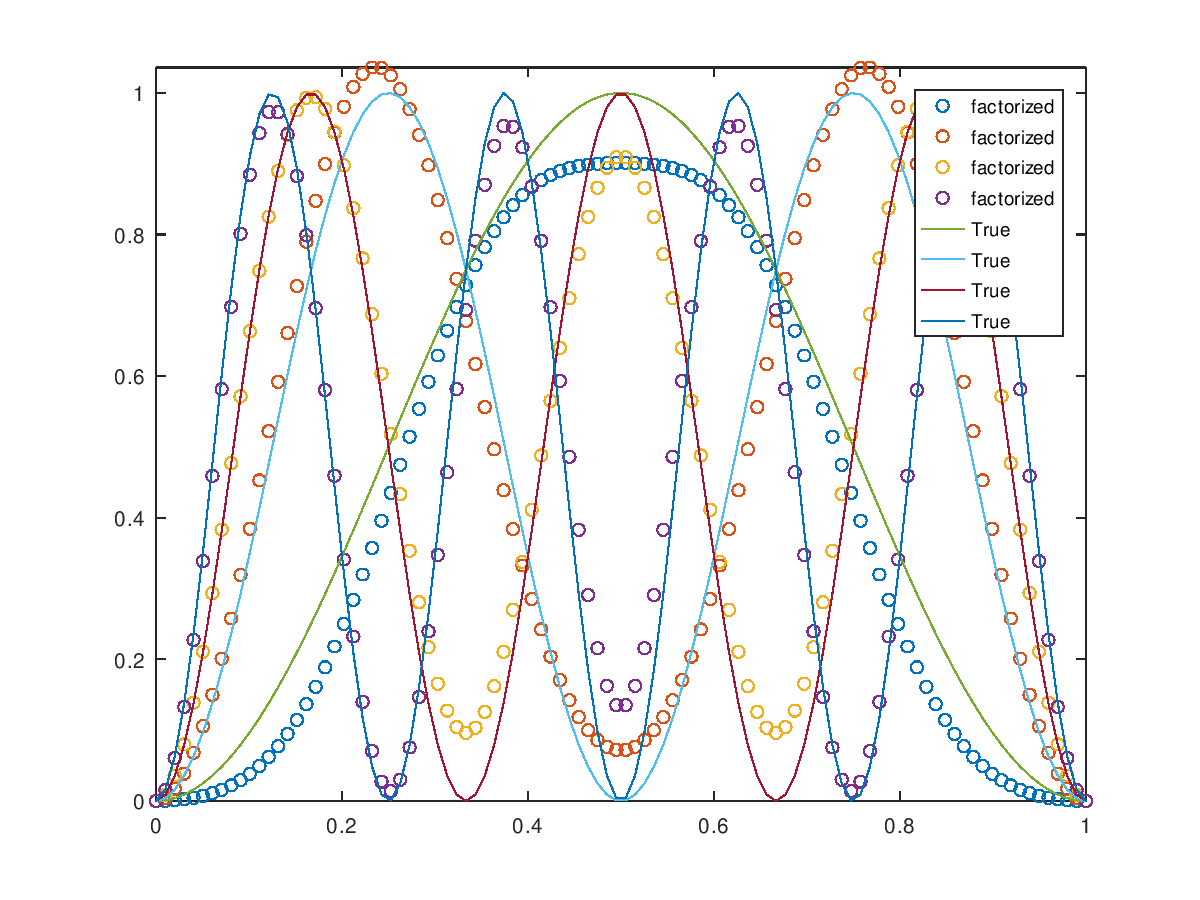
The following code
t = linspace (0,1,100)';
## --- Build hump functions of different frequency
W_true = arrayfun ( @(f)sin(2*pi*f*t).^2, linspace (0.5,2,4), ...
'uniformoutput', false );
W_true = cell2mat (W_true);
## --- Build combinator vectors
c = (1:4)';
H_true = arrayfun ( @(f)circshift(c,f), linspace (0,3,4), ...
'uniformoutput', false );
H_true = cell2mat (H_true);
## --- Mix them
V = W_true*H_true;
## --- Give good inital guesses
Winit = W_true + 0.4*randn(size(W_true));
Hinit = H_true + 0.2*randn(size(H_true));
## --- Factorize
[W H] = nmf_pg(V,'Winit',Winit,'Hinit',Hinit,'Tol',1e-6,'MaxIter',1e3);
disp('True mixer')
disp(H_true)
disp('Rounded factorized mixer')
disp(round(H))
## --- Plot results
plot(t,W,'o;factorized;')
hold on
plot(t,W_true,'-;True;')
hold off
axis tight
Produces the following output
--- Factorizing 100-by-4 matrix into 100-by-4 times 4-by-4 Initial gradient norm = 448.013653 Running main loop, this may take a while. Iterations = 8 Final proj-grad norm = 0.000256 True mixer 1 4 3 2 2 1 4 3 3 2 1 4 4 3 2 1 Rounded factorized mixer 1 4 3 2 2 1 4 3 3 2 1 4 4 3 2 1
and the following figure
| Figure 1 |
|---|
 |
Package: linear-algebra