Navigation

Operators and Keywords

Function List:

C++ API

Function File: [J sigma]= rodmassmatrix (sigma,l, rho)

Mass matrix of one dimensional rod in 3D.

Let q be the configuration vector of the rod, with the first three elements of q being the spatial coordinates (e.g. x,y,z) and the second three elements of q the rotiational coordinates (e.g. Euler angles), then the kinetical energy of the rod is given by T = 1/2 (dqdt)^T kron(J,eye(3)) dqdt

sigma is between 0 and 1. Corresponds to the point in the rod that is being used to indicate the position of the rod in space. If sigma is a string then the value corresponding to the center of mass of the rod. This makes J a diagonal matrix. If sigma is a string the return value of sigma corresponds to the value pointing to the center of mass.

l is the length of the rod. If omitted the rod has unit length.

rho is a function handle to the density of the rod defined in the interval 0,1. The integral of this density equals the mass and is stored in J(1,1). If omitted, the default is a uniform rod with unit mass.

Run demo rodmassmatrix to see some examples.

Demonstration 1

The following code

 barlen  = 2;
 [Jc, s] = rodmassmatrix (0, barlen);

 printf ("Inertia matrix from the extrema : \n")
 disp (Jc)
 printf ("Sigma value to calculate from center of mass : %g \n",s)

 J = rodmassmatrix (s);
 printf ("Inertia matrix from the CoM : \n")
 disp (J)

 J2 = rodmassmatrix ("com");
 tf = all((J2 == J)(:));
 disp (["Are J and J2 equal? " "no"*not(tf) "yes"*tf])

 % ----------------------------------------------------------------------------
 % This example shows the calculations for rod of length 2. First we place one
 % of its extrema in the origin. Then we use the value of sigma provided by
 % the function to do the same calculation form the center of mass.

Produces the following output

Inertia matrix from the extrema : 
   1.00000   1.00000
   1.00000   1.33333
Sigma value to calculate from center of mass : 0.5 
Inertia matrix from the CoM : 
   1.0000e+00   9.0206e-17
   9.0206e-17   8.3333e-02
Are J and J2 equal?

Demonstration 2

The following code

 % A normalized density function
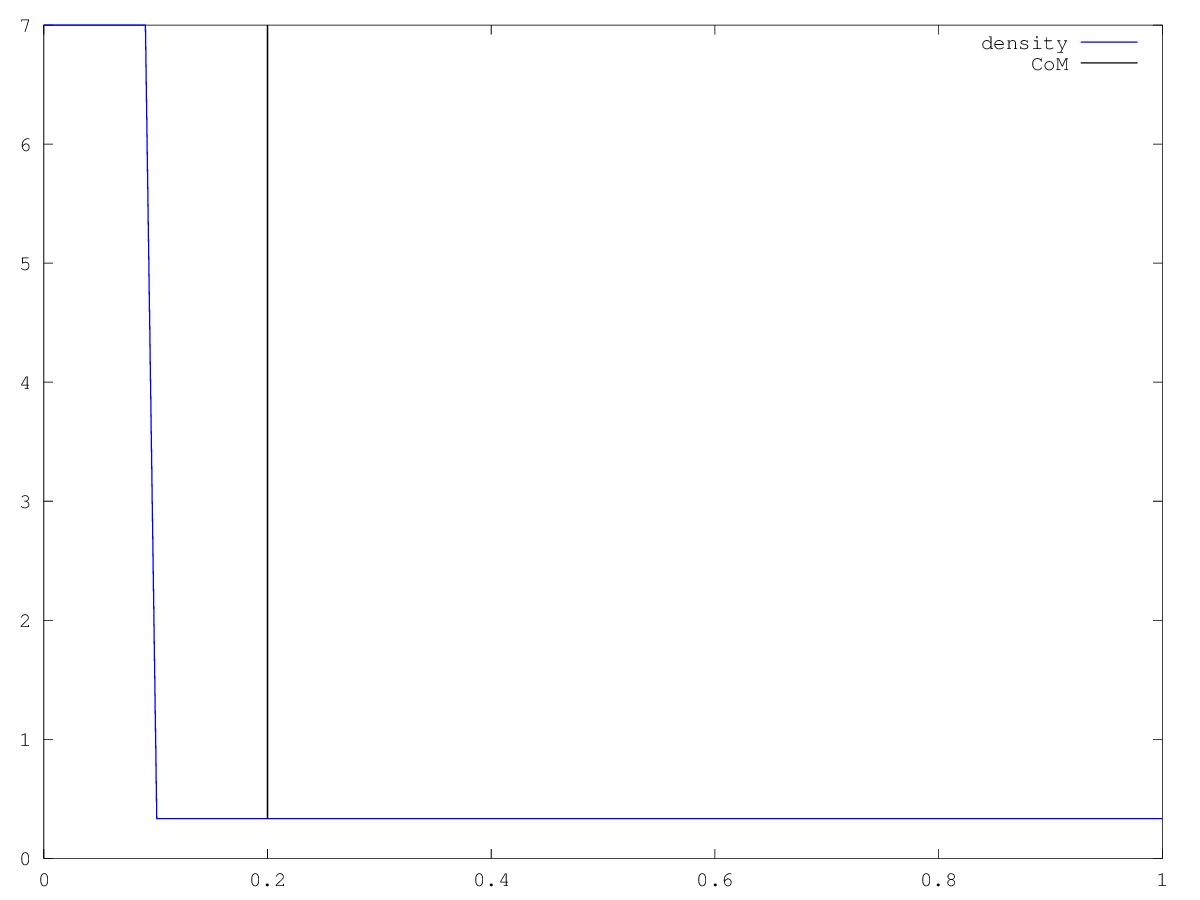
 density = @(x) (0.5*ones(size(x)) + 10*(x<0.1)).*(x>=0 & x<=1)/1.5;
 [Jc, s] = rodmassmatrix (0,1,density);

 printf ("Inertia matrix from the extrema : \n")
 disp (Jc)
 printf ("Sigma value to calculate from center of mass : %g \n",s)
 J = rodmassmatrix (s,1,density);

 printf ("Inertia matrix from the CoM : \n")
 disp (J)

 figure (1)
 clf
 x = linspace (0,1,100)';
 h = plot (x,density(x),'b-;density;');
 set (h,'linewidth',2)
 axis tight
 v = axis();
 hold on
 h = plot ([s s],v([3 4]),'k-;CoM;');
 set (h, 'linewidth', 2);
 hold off
 axis auto
 % ----------------------------------------------------------------------------
 % This example defines a density function with an accumulation of mass near
 % one end of the rod. First we place one of its extrema in the origin. Then
 % we use the value of sigma provided by the function to do the same
 % calculation form the center of mass.

Produces the following output

Inertia matrix from the extrema : 
   1.00000   0.20000
   0.20000   0.11333
Sigma value to calculate from center of mass : 0.2 
Inertia matrix from the CoM : 
   1.0000e+00   2.7977e-07
   2.7977e-07   7.3333e-02

and the following figure

Figure 1