Navigation

Operators and Keywords

Function List:

C++ API

Function File: [mesh] = msh2m_equalize_mesh(mesh)

Apply a baricentric regularization to equalize the size of triangle edges, i.e. move each node to the center of mass of the patch of triangles to which it belongs.

May be useful when distorting a mesh. Type demo msh2m_equalize_mesh to see some examples.

See also: msh2m_displacement_smoothing.

Demonstration 1

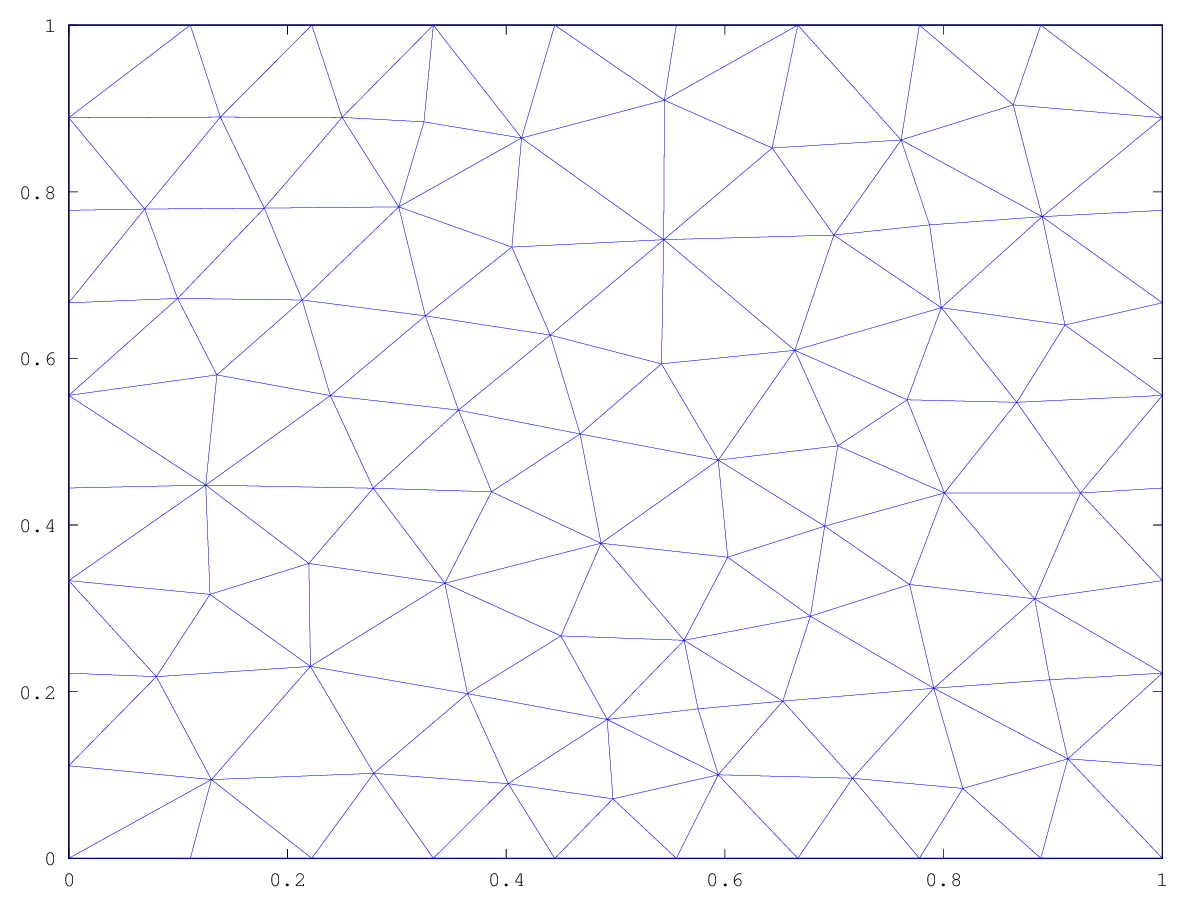
The following code

 ### equalize a structured mesh without moving boundary nodes
 msh = msh2m_structured_mesh(linspace(0,1,10),linspace(0,1,10),1,1:4,"random");
 dnodes = msh2m_nodes_on_sides(msh,1:4);
 varnodes = setdiff([1:columns(msh.p)],dnodes);
 x = msh.p(1,:)';
 y = msh.p(2,:)';
 msh = msh2m_equalize_mesh(msh);
 triplot(msh.t(1:3,:)',msh.p(1,:)',msh.p(2,:)');
 pause(.01)

Produces the following figure

Figure 1

Demonstration 2

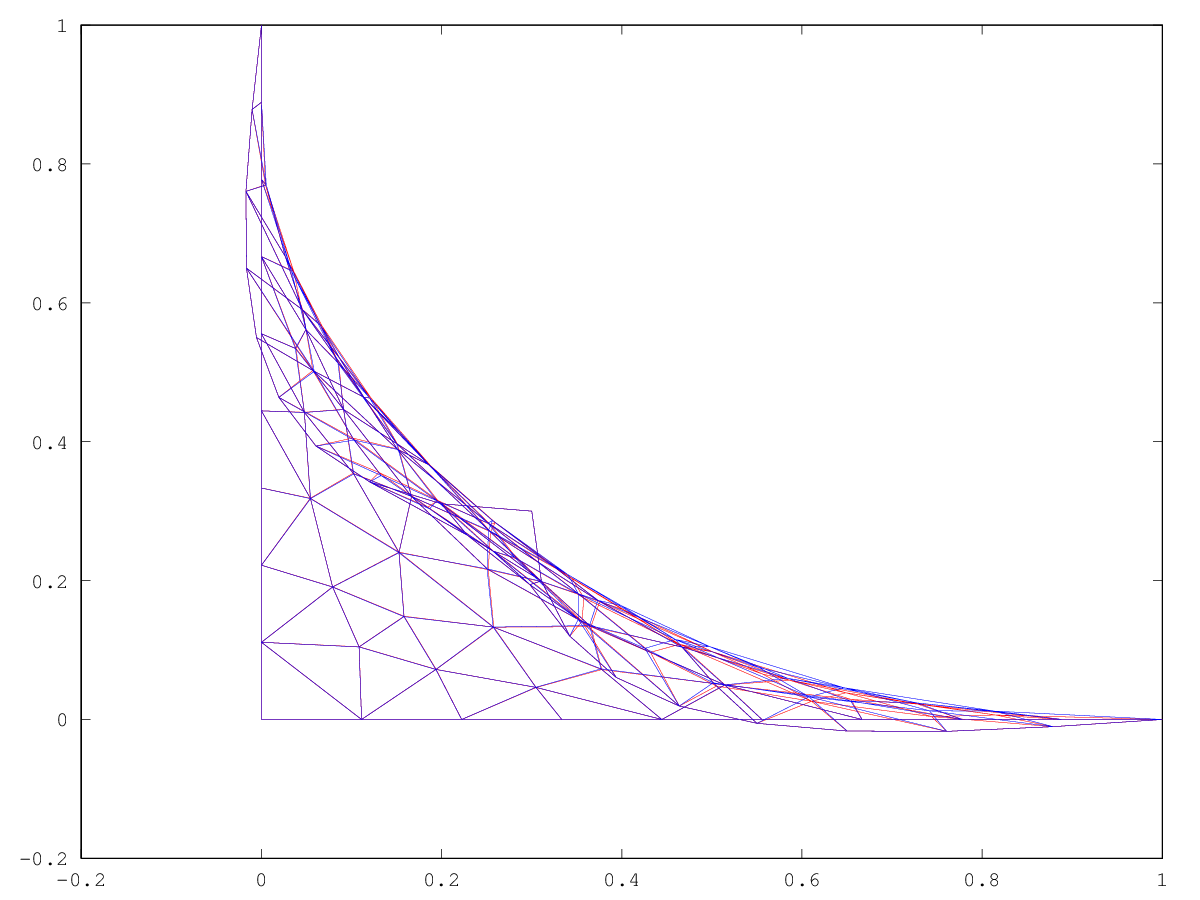
The following code

 ### distort a mesh on a square equalizing at each step
 msh = msh2m_structured_mesh(linspace(0,1,10),linspace(0,1,10),1,1:4,"random");
 dnodes = msh2m_nodes_on_sides(msh,1:4);
 varnodes = setdiff([1:columns(msh.p)],dnodes);
 x = msh.p(1,:)';
 y = msh.p(2,:)';
 dx = dy = zeros(columns(msh.p),1);
 dytot = dxtot = -.7*sin(x(dnodes).*y(dnodes)*pi/2);
 Nsteps = 10;
 for ii=1:Nsteps
  dx(dnodes) = dxtot;
  dy(dnodes) = dytot;
  [Ax,Ay] = msh2m_displacement_smoothing(msh,1);
  dx(varnodes) = Ax(varnodes,varnodes) \ ...
      (-Ax(varnodes,dnodes)*dx(dnodes));
  dy(varnodes) = Ay(varnodes,varnodes) \ ...
  (-Ay(varnodes,dnodes)*dy(dnodes));
  msh.p(1,:) += dx'/Nsteps;
  msh.p(2,:) += dy'/Nsteps;
 triplot(msh.t(1:3,:)',msh.p(1,:)',msh.p(2,:)','r');
  pause(.5)
 x = msh.p(1,:)';
 y = msh.p(2,:)';
 msh = msh2m_equalize_mesh(msh);
 hold on;triplot(msh.t(1:3,:)',msh.p(1,:)',msh.p(2,:)');hold off
  pause(.5)
 endfor

Produces the following figure

Figure 1

Package: msh