Navigation

Operators and Keywords

Function List:

C++ API

Function File: [newmsh] = msh2m_jiggle_mesh(msh,steps)

Equalize the size of triangle edges setting a spring of rest length factor*area along each edge of the mesh and solving for static equilibrium.

The non-linear eqautions of the system obtained are solved via a non-linear Gauss-Seidel method. step is the number of steps of the method to be applied.

May be useful when distorting a mesh, type demo msh2m_jiggle_mesh to see some examples.

See also: msh2m_displacement_smoothing, msh2m_equalize_mesh.

Demonstration 1

The following code

 ### distort a mesh on a square equalizing at each step
 msh = msh2m_structured_mesh(linspace(0,1,10),linspace(0,1,10),1,1:4,"right");
 dnodes = msh2m_nodes_on_sides(msh,1:4);
 varnodes = setdiff([1:columns(msh.p)],dnodes);
 x = msh.p(1,:)';
 y = msh.p(2,:)';
 dx = dy = zeros(columns(msh.p),1);
 dytot = dxtot = -.4*sin(x(dnodes).*y(dnodes)*pi/2);
 Nsteps = 30;
 for ii=1:Nsteps
   dx(dnodes) = dxtot;
   dy(dnodes) = dytot;
   [Ax,Ay] = msh2m_displacement_smoothing(msh,1);
   dx(varnodes) = Ax(varnodes,varnodes) \ ...
       (-Ax(varnodes,dnodes)*dx(dnodes));
   dy(varnodes) = Ay(varnodes,varnodes) \ ...
       (-Ay(varnodes,dnodes)*dy(dnodes));
   msh.p(1,:) += dx'/Nsteps;
   msh.p(2,:) += dy'/Nsteps;
   triplot(msh.t(1:3,:)',msh.p(1,:)',msh.p(2,:)','r');
   pause(.5)
   x   = msh.p(1,:)';
   y   = msh.p(2,:)';
   msh = msh2m_jiggle_mesh(msh,10);
   hold on;
   triplot(msh.t(1:3,:)',msh.p(1,:)',msh.p(2,:)');
   hold off;
   pause(.5)
 endfor

Produces the following figure

Figure 1

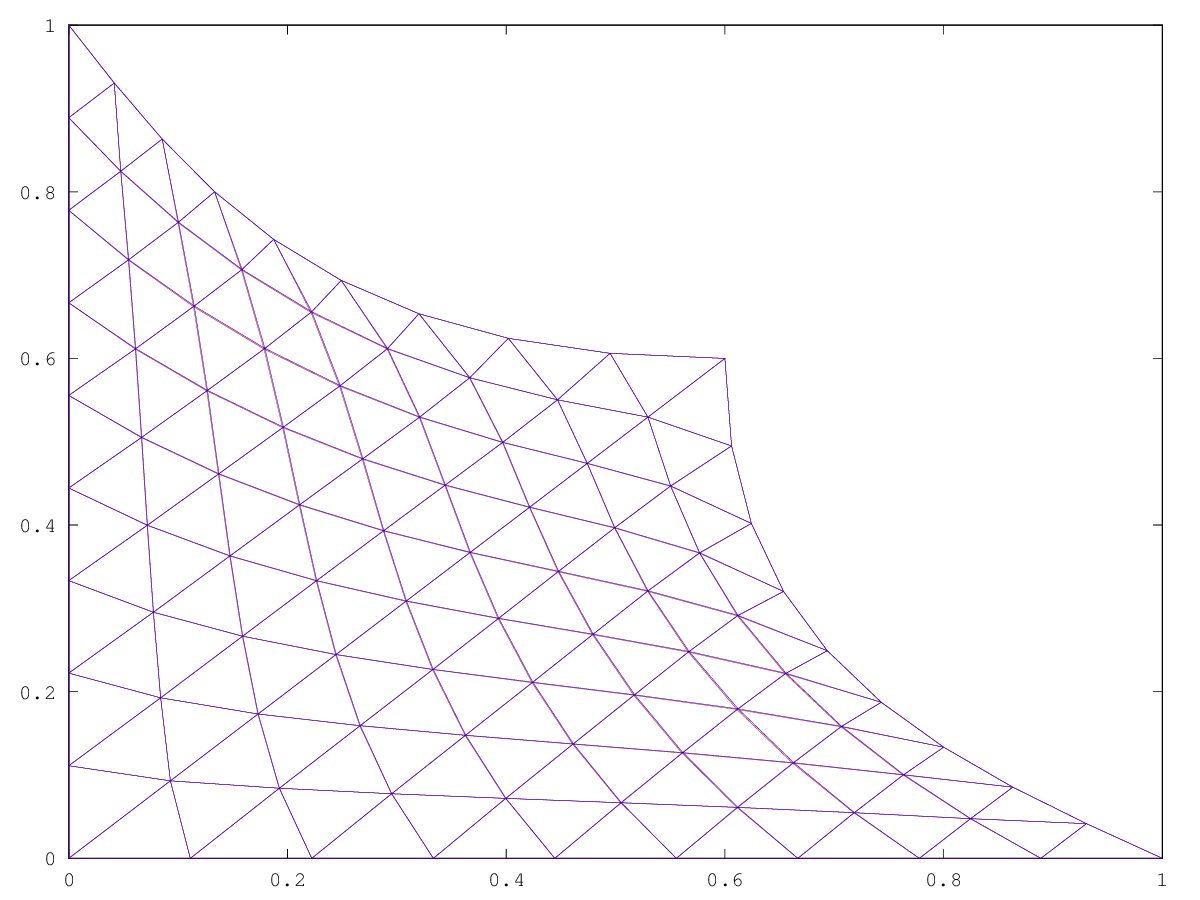Package: msh