NRBBASISFUNDER: NURBS basis functions derivatives
Calling Sequence:
Bu = nrbbasisfunder (u, crv)
[Bu, N] = nrbbasisfunder (u, crv)
[Bu, Bv] = nrbbasisfunder ({u, v}, srf)
[Bu, Bv, N] = nrbbasisfunder ({u, v}, srf)
[Bu, Bv, N] = nrbbasisfunder (pts, srf)
[Bu, Bv, Bw, N] = nrbbasisfunder ({u, v, w}, vol)
[Bu, Bv, Bw, N] = nrbbasisfunder (pts, vol)
INPUT:
u - parametric coordinates along u direction
v - parametric coordinates along v direction
w - parametric coordinates along w direction
pts - array of scattered points in parametric domain, array size: (ndim,num_points)
crv - NURBS curve
srf - NURBS surface
vol - NURBS volume
If the parametric coordinates are given in a cell-array, the values
are computed in a tensor product set of points
OUTPUT:
Bu - Basis functions derivatives WRT direction u
size(Bu)=[npts, prod(nrb.order)]
Bv - Basis functions derivatives WRT direction v
size(Bv) == size(Bu)
Bw - Basis functions derivatives WRT direction w
size(Bw) == size(Bu)
N - Indices of the basis functions that are nonvanishing at each
point. size(N) == size(Bu)
Copyright (C) 2009 Carlo de Falco
Copyright (C) 2016 Rafael Vazquez
This program is free software: you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation, either version 3 of the License, or
(at your option) any later version.
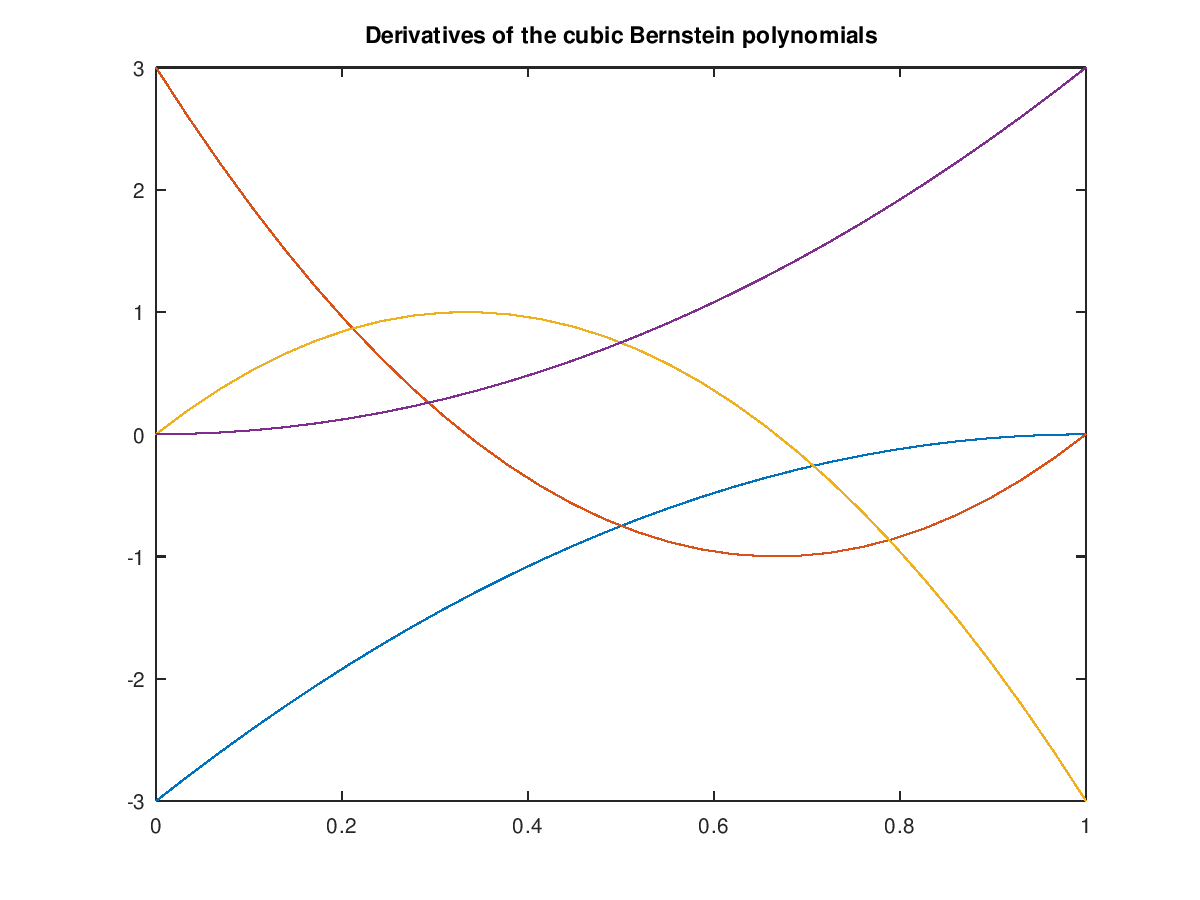
Demonstration 1
The following code
U = [0 0 0 0 1 1 1 1];
x = [0 1/3 2/3 1] ;
y = [0 0 0 0];
w = [1 1 1 1];
nrb = nrbmak ([x;y;y;w], U);
u = linspace(0, 1, 30);
[Bu, id] = nrbbasisfunder (u, nrb);
plot(u, Bu)
title('Derivatives of the cubic Bernstein polynomials')
hold off
Produces the following figure
| Figure 1 |
|---|
 |
Package: nurbs