NRBDERIV: Construct up to the fourth derivative representation of a
NURBS curve, surface or volume.
Calling Sequence:
ders = nrbderiv (nrb);
[ders, ders2] = nrbderiv (nrb);
[ders, ders2, ders3] = nrbderiv (nrb);
[ders, ders2, ders, ders4] = nrbderiv (nrb);
INPUT:
nrb : NURBS data structure, see nrbmak.
OUTPUT:
ders: A data structure that represents the first
derivatives of a NURBS curve, surface or volume.
ders2: A data structure that represents the second
derivatives of a NURBS curve, surface or volume.
ders3: A data structure that represents the third
derivatives of a NURBS curve, surface or volume. (only surface
for now)
ders4: A data structure that represents the fourth
derivatives of a NURBS curve, surface or volume. (only surface
for now)
Description:
The derivatives of a B-Spline are themselves a B-Spline of lower degree,
giving an efficient means of evaluating multiple derivatives. However,
although the same approach can be applied to NURBS, the situation for
NURBS is more complex. We have followed in this function the same idea
that was already used for the first derivative in the function nrbderiv.
The second derivative data structure can be evaluated later with the
function nrbdeval.
See also:
nrbdeval
Copyright (C) 2000 Mark Spink
Copyright (C) 2010 Carlo de Falco
Copyright (C) 2010, 2011 Rafael Vazquez
Copyright (C) 2018 Luca Coradello
This program is free software: you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation, either version 3 of the License, or
(at your option) any later version.
Demonstration 1
The following code
crv = nrbtestcrv;
nrbplot(crv,48);
title('First derivatives along a test curve.');
tt = linspace(0.0,1.0,9);
dcrv = nrbderiv(crv);
[p1, dp] = nrbdeval(crv,dcrv,tt);
p2 = vecnormalize(dp);
hold on;
plot(p1(1,:),p1(2,:),'ro');
h = quiver(p1(1,:),p1(2,:),p2(1,:),p2(2,:),0);
set(h,'Color','black');
hold off;
Produces the following figure
| Figure 1 |
|---|
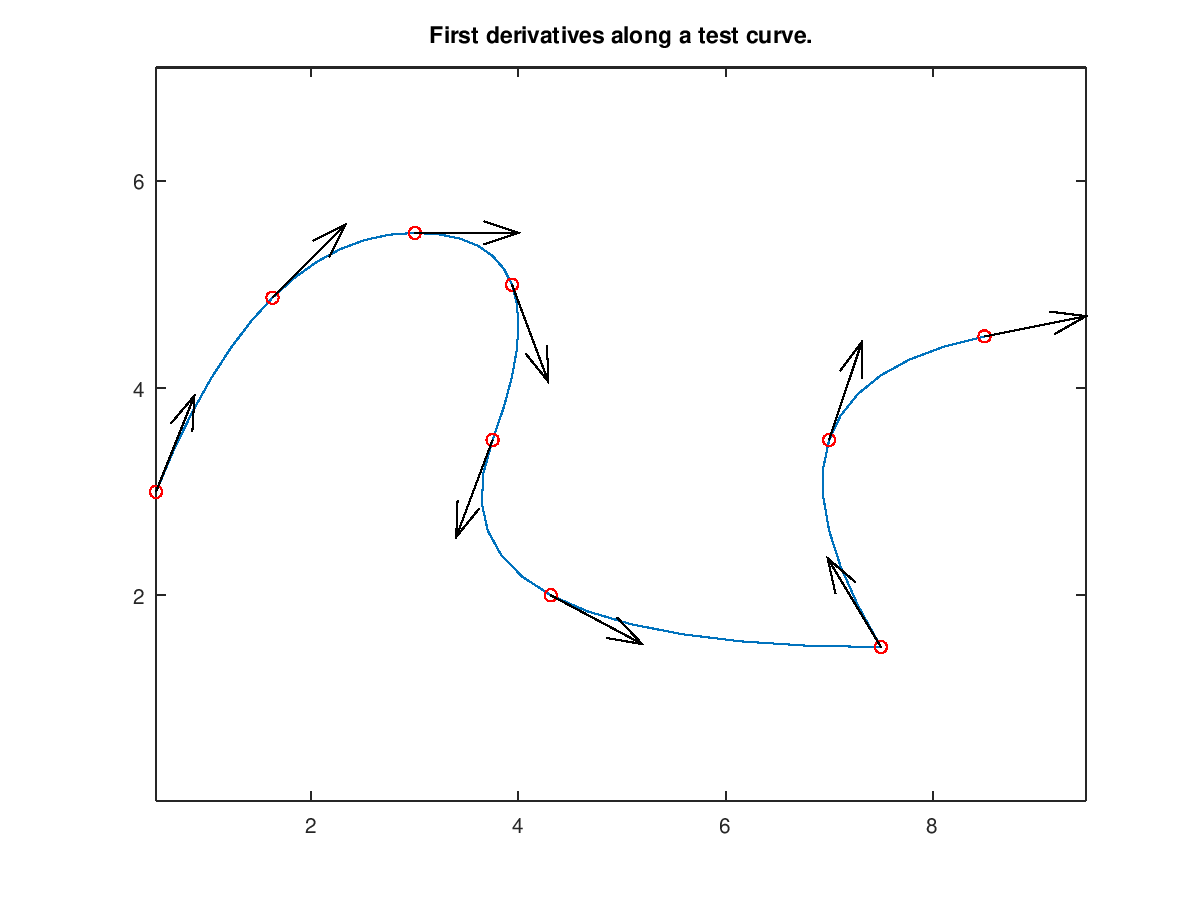 |
Demonstration 2
The following code
srf = nrbtestsrf;
p = nrbeval(srf,{linspace(0.0,1.0,20) linspace(0.0,1.0,20)});
h = surf(squeeze(p(1,:,:)),squeeze(p(2,:,:)),squeeze(p(3,:,:)));
set(h,'FaceColor','blue','EdgeColor','blue');
title('First derivatives over a test surface.');
npts = 5;
tt = linspace(0.0,1.0,npts);
dsrf = nrbderiv(srf);
[p1, dp] = nrbdeval(srf, dsrf, {tt, tt});
up2 = vecnormalize(dp{1});
vp2 = vecnormalize(dp{2});
hold on;
plot3(p1(1,:),p1(2,:),p1(3,:),'ro');
h1 = quiver3(p1(1,:),p1(2,:),p1(3,:),up2(1,:),up2(2,:),up2(3,:));
h2 = quiver3(p1(1,:),p1(2,:),p1(3,:),vp2(1,:),vp2(2,:),vp2(3,:));
set(h1,'Color','black');
set(h2,'Color','black');
hold off;
Produces the following figure
| Figure 1 |
|---|
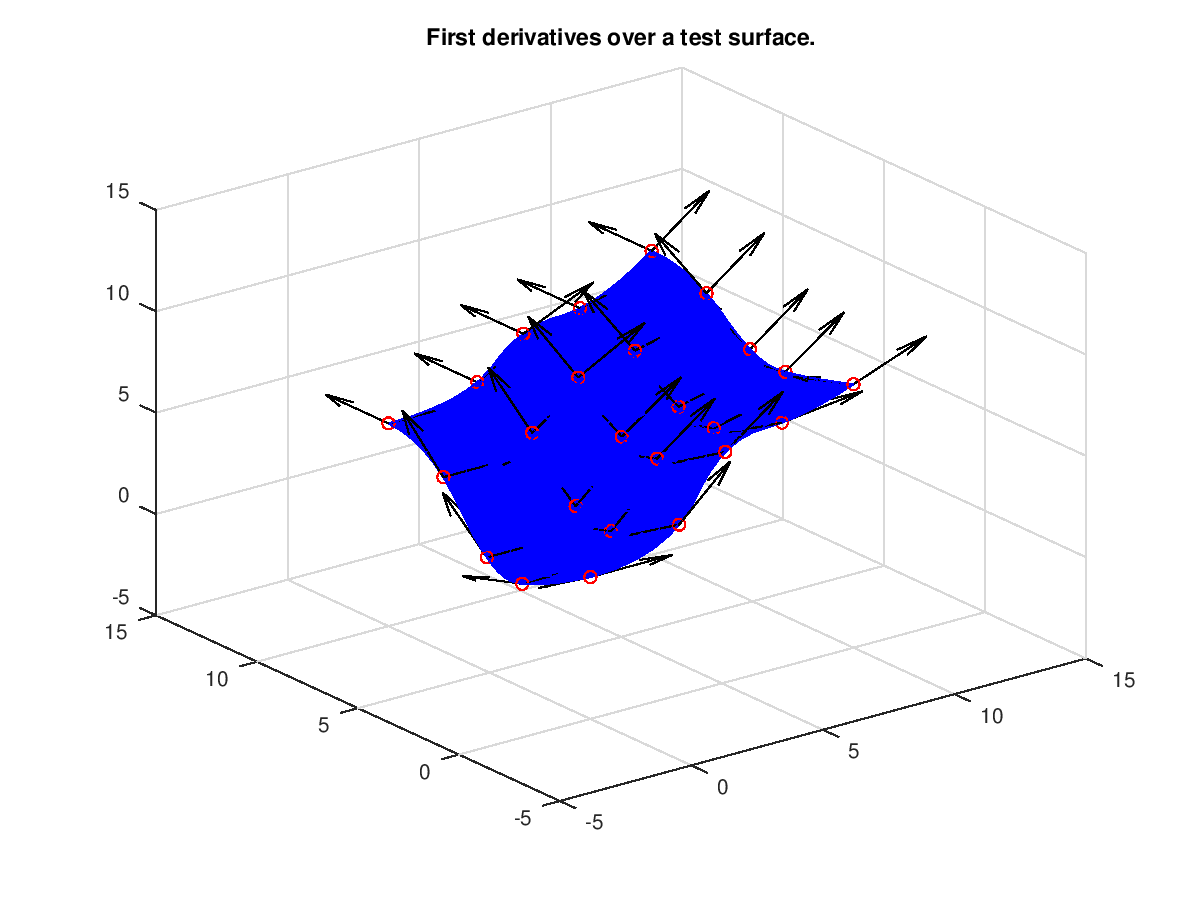 |
Package: nurbs