NRBDEVAL: Evaluation of the derivative and second derivatives of NURBS curve, surface or volume.
[pnt, jac] = nrbdeval (crv, dcrv, tt)
[pnt, jac] = nrbdeval (srf, dsrf, {tu tv})
[pnt, jac] = nrbdeval (vol, dvol, {tu tv tw})
[pnt, jac, hess] = nrbdeval (crv, dcrv, dcrv2, tt)
[pnt, jac, hess] = nrbdeval (srf, dsrf, dsrf2, {tu tv})
[pnt, jac, hess] = nrbdeval (vol, dvol, dvol2, {tu tv tw})
[pnt, jac, hess, third_der] = nrbdeval (crv, dcrv, dcrv2, dcrv3, tt)
[pnt, jac, hess, third_der] = nrbdeval (srf, dsrf, dsrf2, dsrf3, {tu tv})
[pnt, jac, hess, third_der, fourth_der] = nrbdeval (crv, dcrv, dcrv2, dcrv3, dcrv4, tt)
[pnt, jac, hess, third_der, fourth_der] = nrbdeval (srf, dsrf, dsrf2, dsrf3, dsrf4, {tu tv})
INPUTS:
crv, srf, vol - original NURBS curve, surface or volume.
dcrv, dsrf, dvol - NURBS derivative representation of crv, srf
or vol (see nrbderiv2)
dcrv2, dsrf2, dvol2 - NURBS second derivative representation of crv,
srf or vol (see nrbderiv2)
dcrv3, dsrf3, dvol3 - NURBS third derivative representation of crv,
srf or vol (see nrbderiv)
dcrv4, dsrf4, dvol4 - NURBS fourth derivative representation of crv,
srf or vol (see nrbderiv)
tt - parametric evaluation points
If the nurbs is a surface or a volume then tt is a cell
{tu, tv} or {tu, tv, tw} are the parametric coordinates
OUTPUT:
pnt - evaluated points.
jac - evaluated first derivatives (Jacobian).
hess - evaluated second derivatives (Hessian).
third_der - evaluated third derivatives
fourth_der - evaluated fourth derivatives
Copyright (C) 2000 Mark Spink
Copyright (C) 2010 Carlo de Falco
Copyright (C) 2010, 2011 Rafael Vazquez
Copyright (C) 2018 Luca Coradello
This program is free software: you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation, either version 3 of the License, or
(at your option) any later version.
Demonstration 1
The following code
crv = nrbtestcrv;
nrbplot(crv,48);
title('First derivatives along a test curve.');
tt = linspace(0.0,1.0,9);
dcrv = nrbderiv(crv);
[p1, dp] = nrbdeval(crv,dcrv,tt);
p2 = vecnormalize(dp);
hold on;
plot(p1(1,:),p1(2,:),'ro');
h = quiver(p1(1,:),p1(2,:),p2(1,:),p2(2,:),0);
set(h,'Color','black');
hold off;
Produces the following figure
| Figure 1 |
|---|
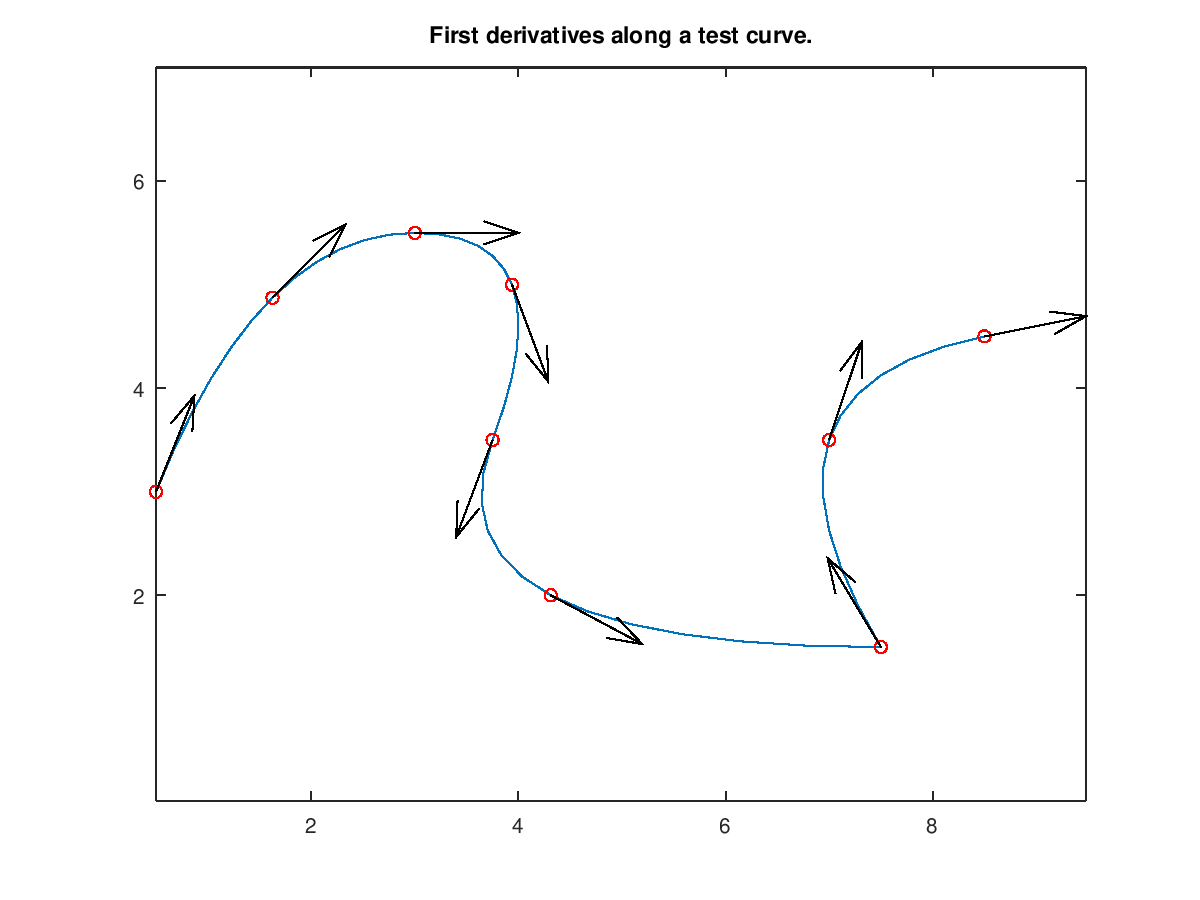 |
Demonstration 2
The following code
srf = nrbtestsrf;
p = nrbeval(srf,{linspace(0.0,1.0,20) linspace(0.0,1.0,20)});
h = surf(squeeze(p(1,:,:)),squeeze(p(2,:,:)),squeeze(p(3,:,:)));
set(h,'FaceColor','blue','EdgeColor','blue');
title('First derivatives over a test surface.');
npts = 5;
tt = linspace(0.0,1.0,npts);
dsrf = nrbderiv(srf);
[p1, dp] = nrbdeval(srf, dsrf, {tt, tt});
up2 = vecnormalize(dp{1});
vp2 = vecnormalize(dp{2});
hold on;
plot3(p1(1,:),p1(2,:),p1(3,:),'ro');
h1 = quiver3(p1(1,:),p1(2,:),p1(3,:),up2(1,:),up2(2,:),up2(3,:));
h2 = quiver3(p1(1,:),p1(2,:),p1(3,:),vp2(1,:),vp2(2,:),vp2(3,:));
set(h1,'Color','black');
set(h2,'Color','black');
hold off;
Produces the following figure
| Figure 1 |
|---|
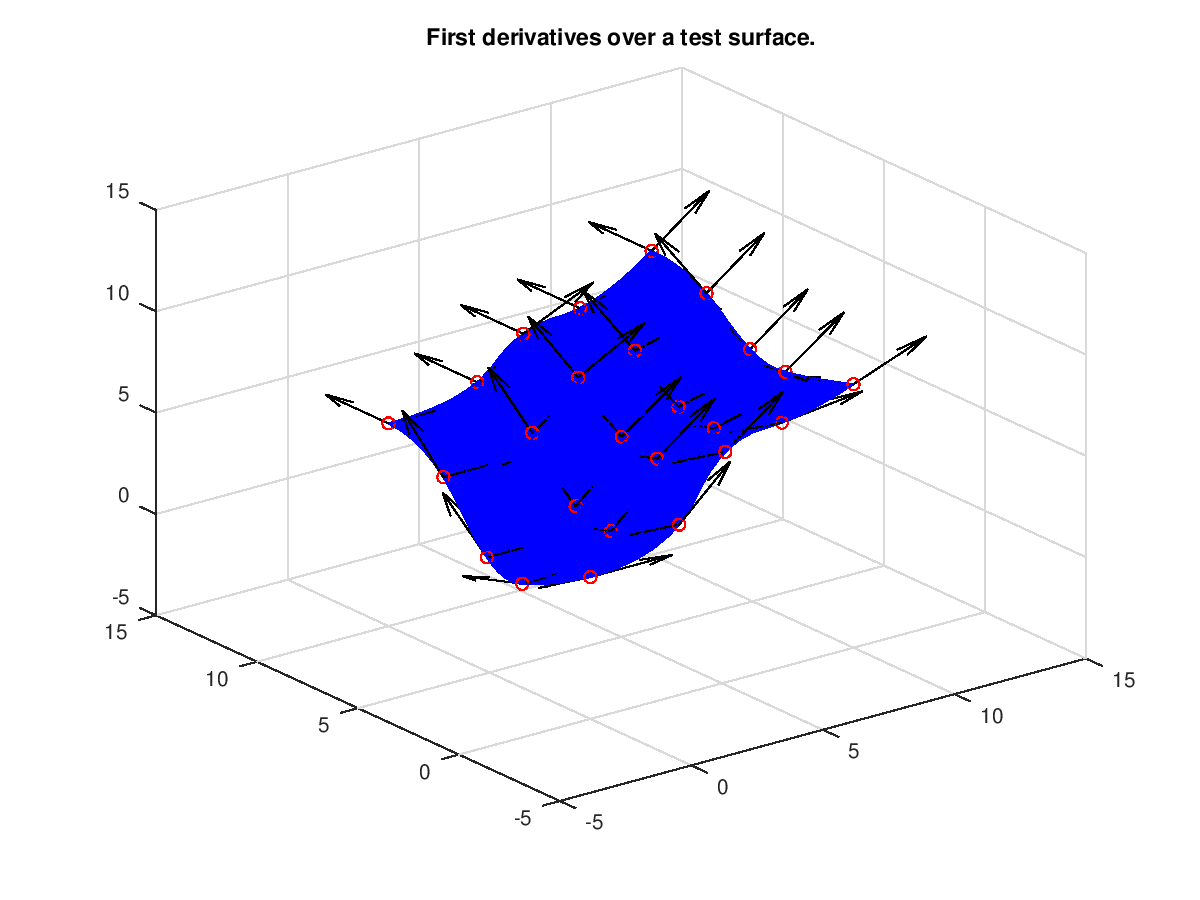 |
Package: nurbs