NRBREVOLVE: Construct a NURBS surface by revolving a NURBS curve, or
construct a NURBS volume by revolving a NURBS surface.
Calling Sequence:
srf = nrbrevolve(crv,pnt,vec[,ang])
INPUT:
crv : NURBS curve or surface to revolve, see nrbmak.
pnt : Coordinates of the point used to define the axis
of rotation.
vec : Vector defining the direction of the rotation axis.
ang : Angle to revolve the curve, default 2*pi
OUTPUT:
srf : constructed surface or volume
Description:
Construct a NURBS surface by revolving the profile NURBS curve around
an axis defined by a point and vector.
Examples:
Construct a sphere by rotating a semicircle around a x-axis.
crv = nrbcirc(1.0,[0 0 0],0,pi);
srf = nrbrevolve(crv,[0 0 0],[1 0 0]);
nrbplot(srf,[20 20]);
NOTE:
The algorithm:
1) vectrans the point to the origin (0,0,0)
2) rotate the vector into alignment with the z-axis
for each control point along the curve
3) determine the radius and angle of control
point to the z-axis
4) construct a circular arc in the x-y plane with
this radius and start angle and sweep angle theta
5) combine the arc and profile, coefs and weights.
next control point
6) rotate and vectrans the surface back into position
by reversing 1 and 2.
Copyright (C) 2000 Mark Spink
Copyright (C) 2010 Rafael Vazquez
This program is free software: you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation, either version 3 of the License, or
(at your option) any later version.
Demonstration 1
The following code
sphere = nrbrevolve(nrbcirc(1,[],0.0,pi),[0.0 0.0 0.0],[1.0 0.0 0.0]);
nrbplot(sphere,[40 40],'light','on');
title('Ball and tori - surface construction by revolution');
hold on;
torus = nrbrevolve(nrbcirc(0.2,[0.9 1.0]),[0.0 0.0 0.0],[1.0 0.0 0.0]);
nrbplot(torus,[40 40],'light','on');
nrbplot(nrbtform(torus,vectrans([-1.8])),[20 10],'light','on');
hold off;
Produces the following figure
| Figure 1 |
|---|
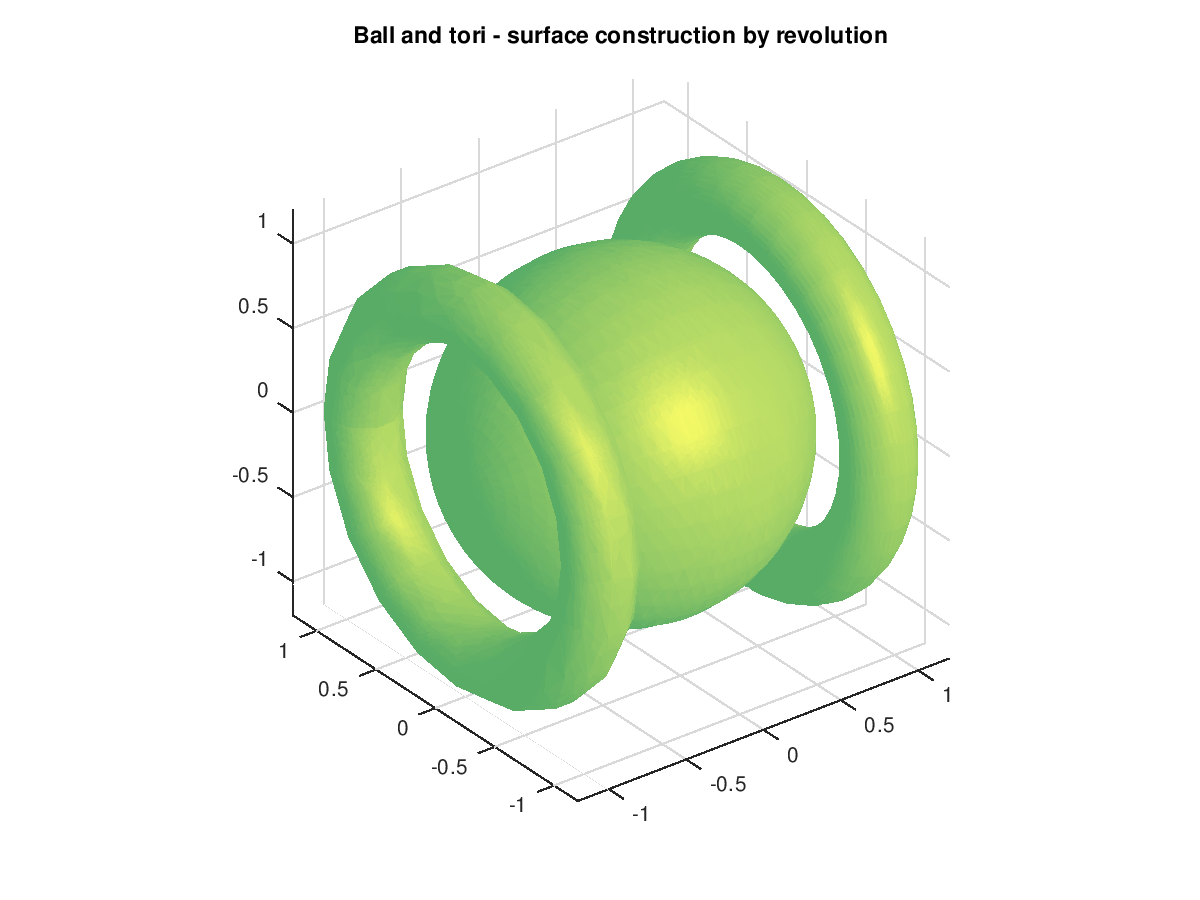 |
Demonstration 2
The following code
pnts = [3.0 5.5 5.5 1.5 1.5 4.0 4.5;
0.0 0.0 0.0 0.0 0.0 0.0 0.0;
0.5 1.5 4.5 3.0 7.5 6.0 8.5];
crv = nrbmak(pnts,[0 0 0 1/4 1/2 3/4 3/4 1 1 1]);
xx = vecrotz(25*pi/180)*vecroty(15*pi/180)*vecrotx(20*pi/180);
nrb = nrbtform(crv,vectrans([5 5])*xx);
pnt = [5 5 0]';
vec = xx*[0 0 1 1]';
srf = nrbrevolve(nrb,pnt,vec(1:3));
p = nrbeval(srf,{linspace(0.0,1.0,100) linspace(0.0,1.0,100)});
surfl(squeeze(p(1,:,:)),squeeze(p(2,:,:)),squeeze(p(3,:,:)));
title('Construct of a 3D surface by revolution of a curve.');
shading interp;
colormap(copper);
axis equal;
hold off
Produces the following figure
| Figure 1 |
|---|
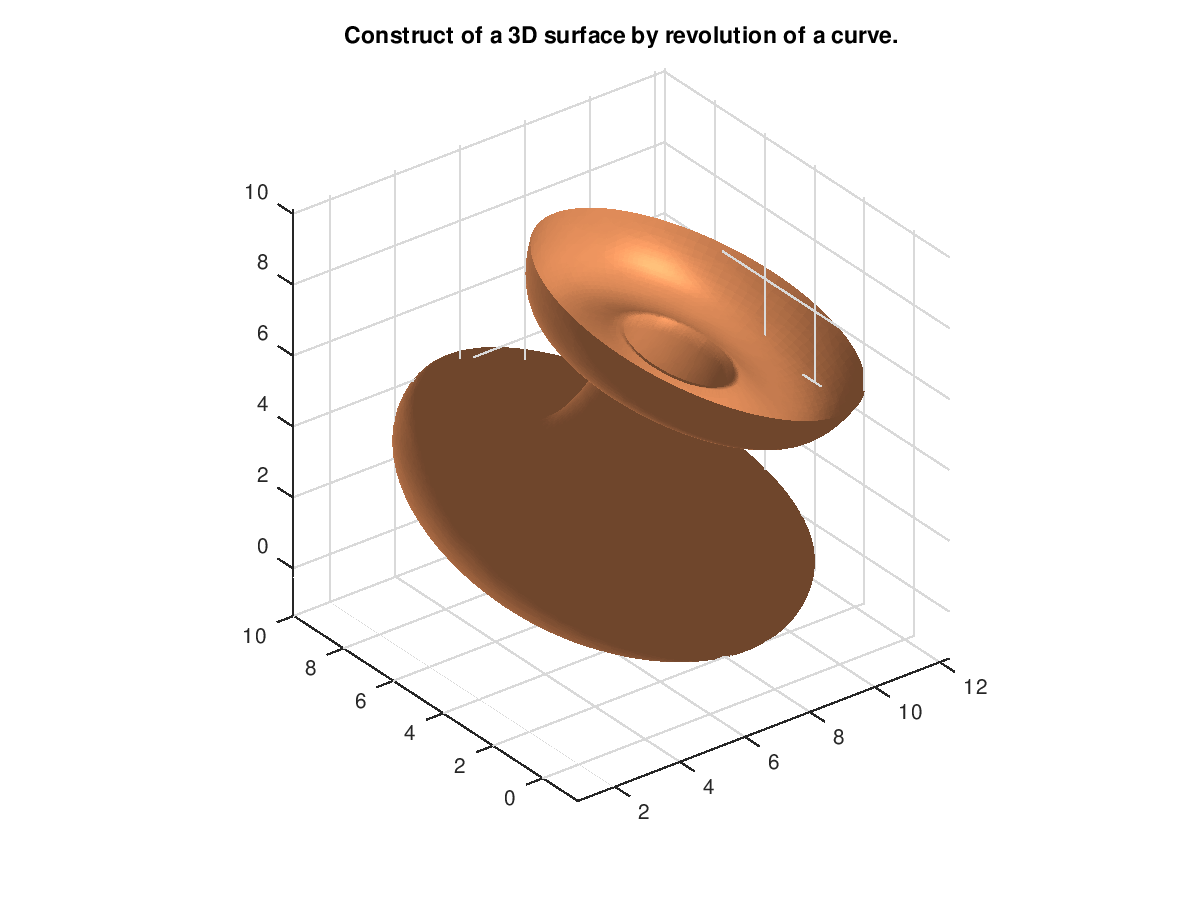 |
Demonstration 3
The following code
crv1 = nrbcirc(1,[0 0],0, pi/2); crv2 = nrbcirc(2,[0 0],0, pi/2); srf = nrbruled (crv1, crv2); srf = nrbtform (srf, [1 0 0 0; 0 1 0 1; 0 0 1 0; 0 0 0 1]); vol = nrbrevolve (srf, [0 0 0], [1 0 0], pi/2); nrbplot(vol, [30 30 30], 'light', 'on')
Produces the following figure
| Figure 1 |
|---|
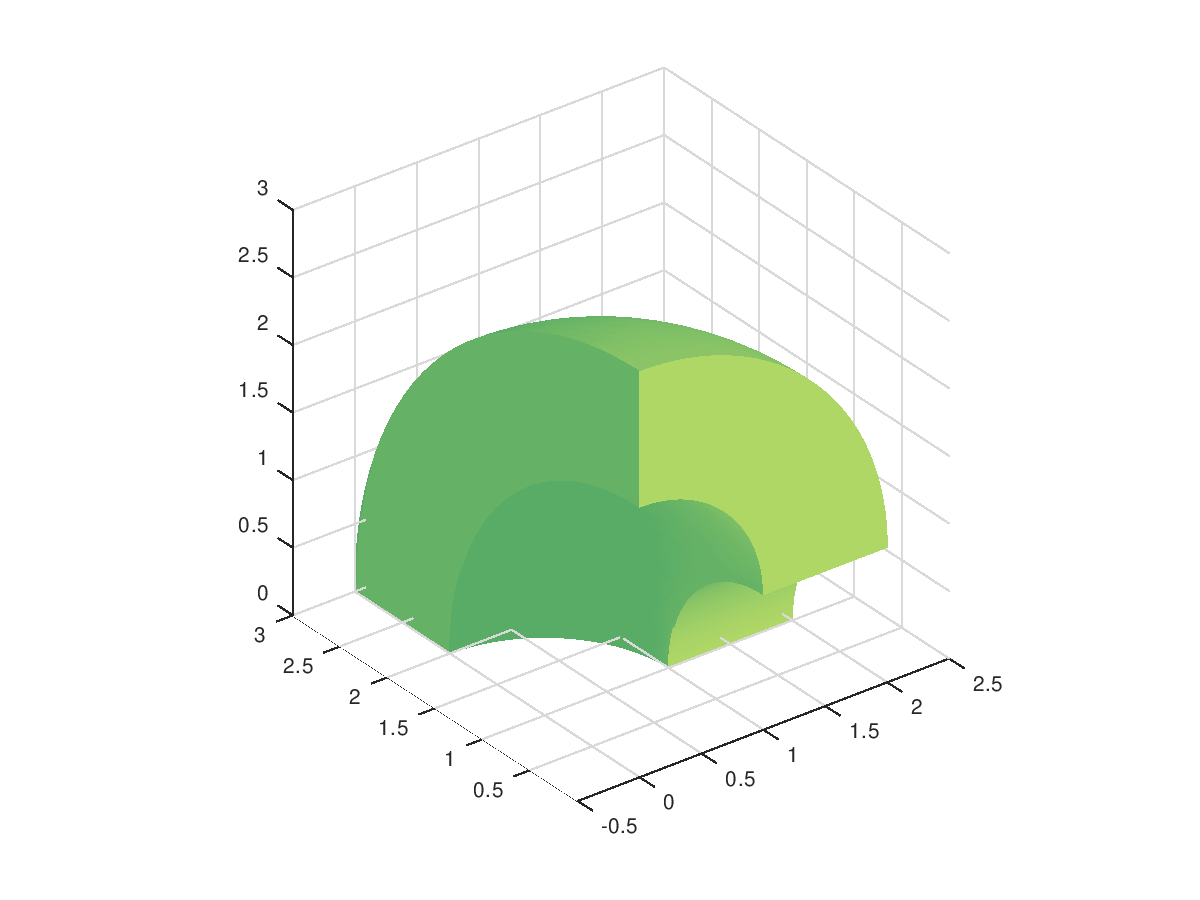 |
Package: nurbs