Navigation

Operators and Keywords

Function List:

C++ API

: zi = griddata (x, y, z, xi, yi)
: zi = griddata (x, y, z, xi, yi, method)
: [xi, yi, zi] = griddata (…)

Generate a regular mesh from irregular data using interpolation.

The function is defined by z = f (x, y). Inputs x, y, z are vectors of the same length or x, y are vectors and z is matrix.

The interpolation points are all (xi, yi). If xi, yi are vectors then they are made into a 2-D mesh.

The interpolation method can be "nearest", "cubic" or "linear". If method is omitted it defaults to "linear".

See also: griddata3, griddatan, delaunay.

Demonstration 1

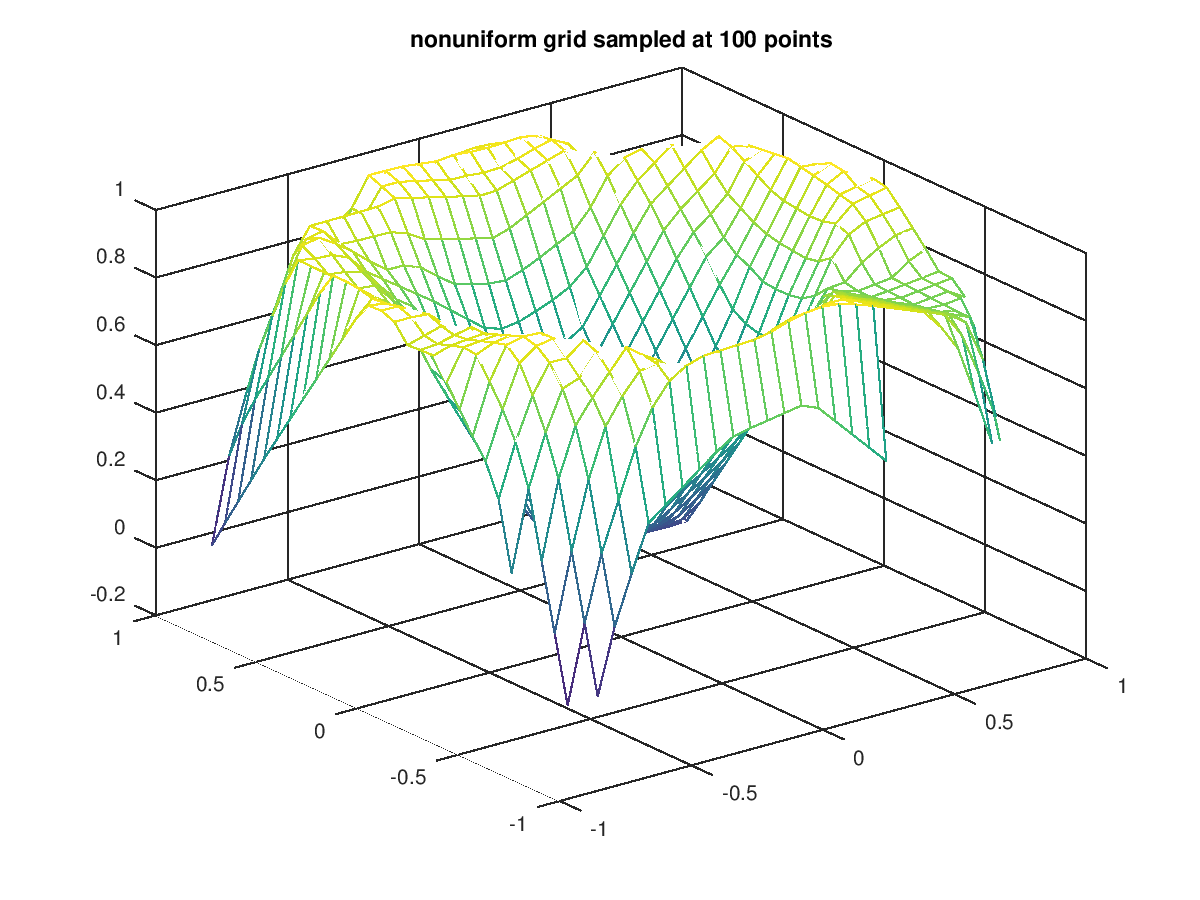
The following code

 clf;
 colormap ("default");
 x = 2*rand (100,1) - 1;
 y = 2*rand (size (x)) - 1;
 z = sin (2*(x.^2 + y.^2));
 [xx,yy] = meshgrid (linspace (-1,1,32));
 zz = griddata (x,y,z,xx,yy);
 mesh (xx, yy, zz);
 title ("nonuniform grid sampled at 100 points");

Produces the following figure

Figure 1

Demonstration 2

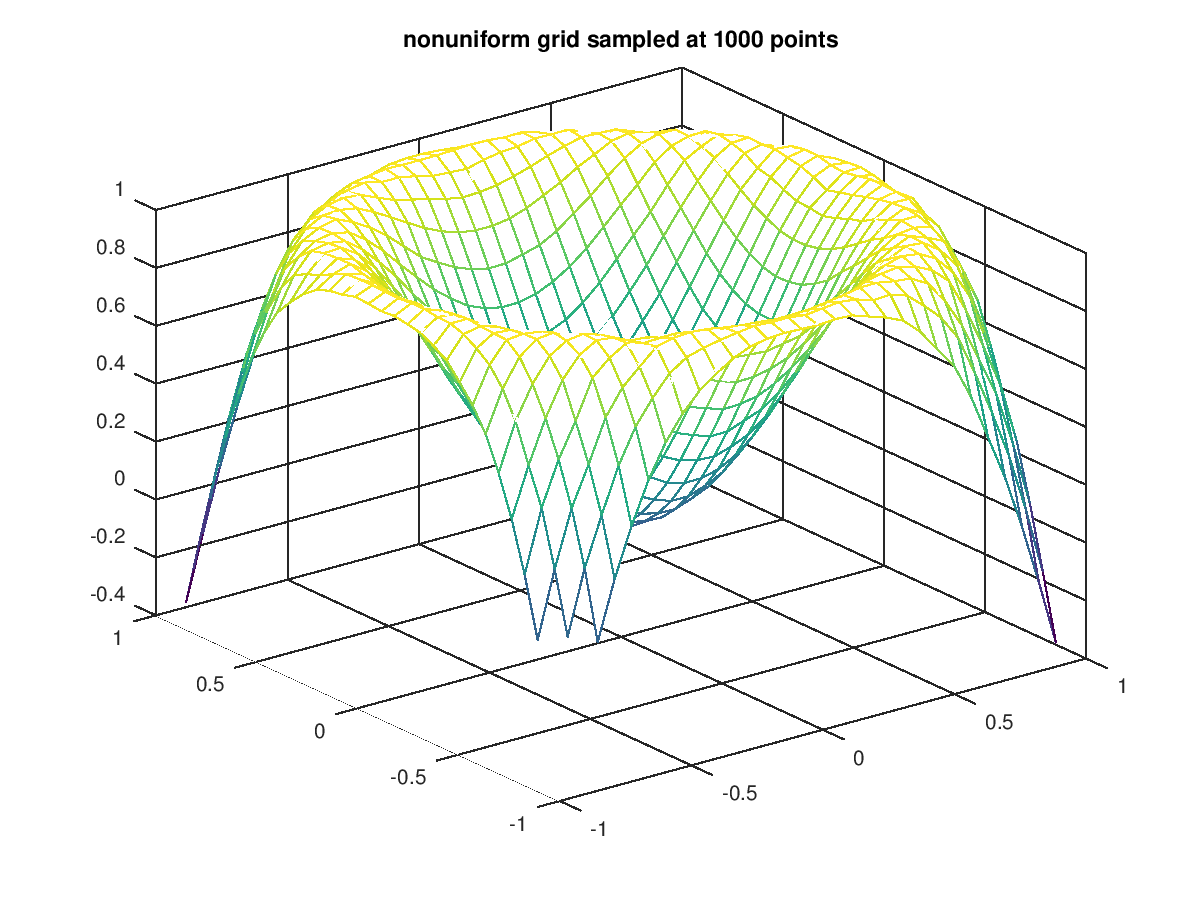
The following code

 clf;
 colormap ("default");
 x = 2*rand (1000,1) - 1;
 y = 2*rand (size (x)) - 1;
 z = sin (2*(x.^2 + y.^2));
 [xx,yy] = meshgrid (linspace (-1,1,32));
 zz = griddata (x,y,z,xx,yy);
 mesh (xx, yy, zz);
 title ("nonuniform grid sampled at 1000 points");

Produces the following figure

Figure 1

Demonstration 3

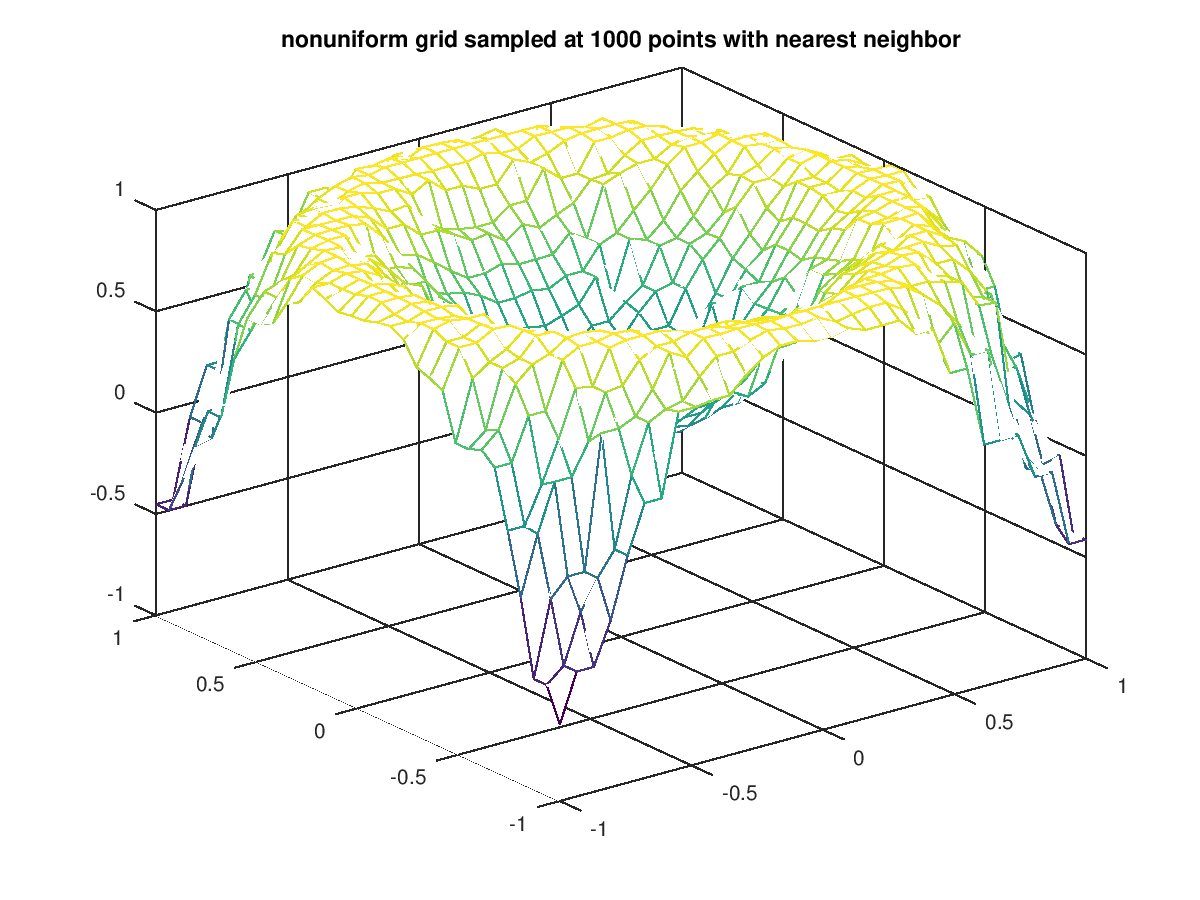
The following code

 clf;
 colormap ("default");
 x = 2*rand (1000,1) - 1;
 y = 2*rand (size (x)) - 1;
 z = sin (2*(x.^2 + y.^2));
 [xx,yy] = meshgrid (linspace (-1,1,32));
 zz = griddata (x,y,z,xx,yy,"nearest");
 mesh (xx, yy, zz);
 title ("nonuniform grid sampled at 1000 points with nearest neighbor");

Produces the following figure

Figure 1

Package: octave