Navigation

Operators and Keywords

Function List:

C++ API

: yi = interp1 (x, y, xi)
: yi = interp1 (y, xi)
: yi = interp1 (…, method)
: yi = interp1 (…, extrap)
: yi = interp1 (…, "left")
: yi = interp1 (…, "right")
: pp = interp1 (…, "pp")

One-dimensional interpolation.

Interpolate input data to determine the value of yi at the points xi. If not specified, x is taken to be the indices of y (1:length (y)). If y is a matrix or an N-dimensional array, the interpolation is performed on each column of y.

The interpolation method is one of:

"nearest"

Return the nearest neighbor.

"previous"

Return the previous neighbor.

"next"

Return the next neighbor.

"linear" (default)

Linear interpolation from nearest neighbors.

"pchip"

Piecewise cubic Hermite interpolating polynomial—shape-preserving interpolation with smooth first derivative.

"cubic"

Cubic interpolation (same as "pchip").

"spline"

Cubic spline interpolation—smooth first and second derivatives throughout the curve.

Adding ’*’ to the start of any method above forces interp1 to assume that x is uniformly spaced, and only x(1) and x(2) are referenced. This is usually faster, and is never slower. The default method is "linear".

If extrap is the string "extrap", then extrapolate values beyond the endpoints using the current method. If extrap is a number, then replace values beyond the endpoints with that number. When unspecified, extrap defaults to NA.

If the string argument "pp" is specified, then xi should not be supplied and interp1 returns a piecewise polynomial object. This object can later be used with ppval to evaluate the interpolation. There is an equivalence, such that ppval (interp1 (x, y, method, "pp"), xi) == interp1 (x, y, xi, method, "extrap").

Duplicate points in x specify a discontinuous interpolant. There may be at most 2 consecutive points with the same value. If x is increasing, the default discontinuous interpolant is right-continuous. If x is decreasing, the default discontinuous interpolant is left-continuous. The continuity condition of the interpolant may be specified by using the options "left" or "right" to select a left-continuous or right-continuous interpolant, respectively. Discontinuous interpolation is only allowed for "nearest" and "linear" methods; in all other cases, the x-values must be unique.

An example of the use of interp1 is 

xf = [0:0.05:10];
yf = sin (2*pi*xf/5);
xp = [0:10];
yp = sin (2*pi*xp/5);
lin = interp1 (xp, yp, xf);
near = interp1 (xp, yp, xf, "nearest");
pch = interp1 (xp, yp, xf, "pchip");
spl = interp1 (xp, yp, xf, "spline");
plot (xf,yf,"r", xf,near,"g", xf,lin,"b", xf,pch,"c", xf,spl,"m",
      xp,yp,"r*");
legend ("original", "nearest", "linear", "pchip", "spline");

See also: pchip, spline, interpft, interp2, interp3, interpn.

Demonstration 1

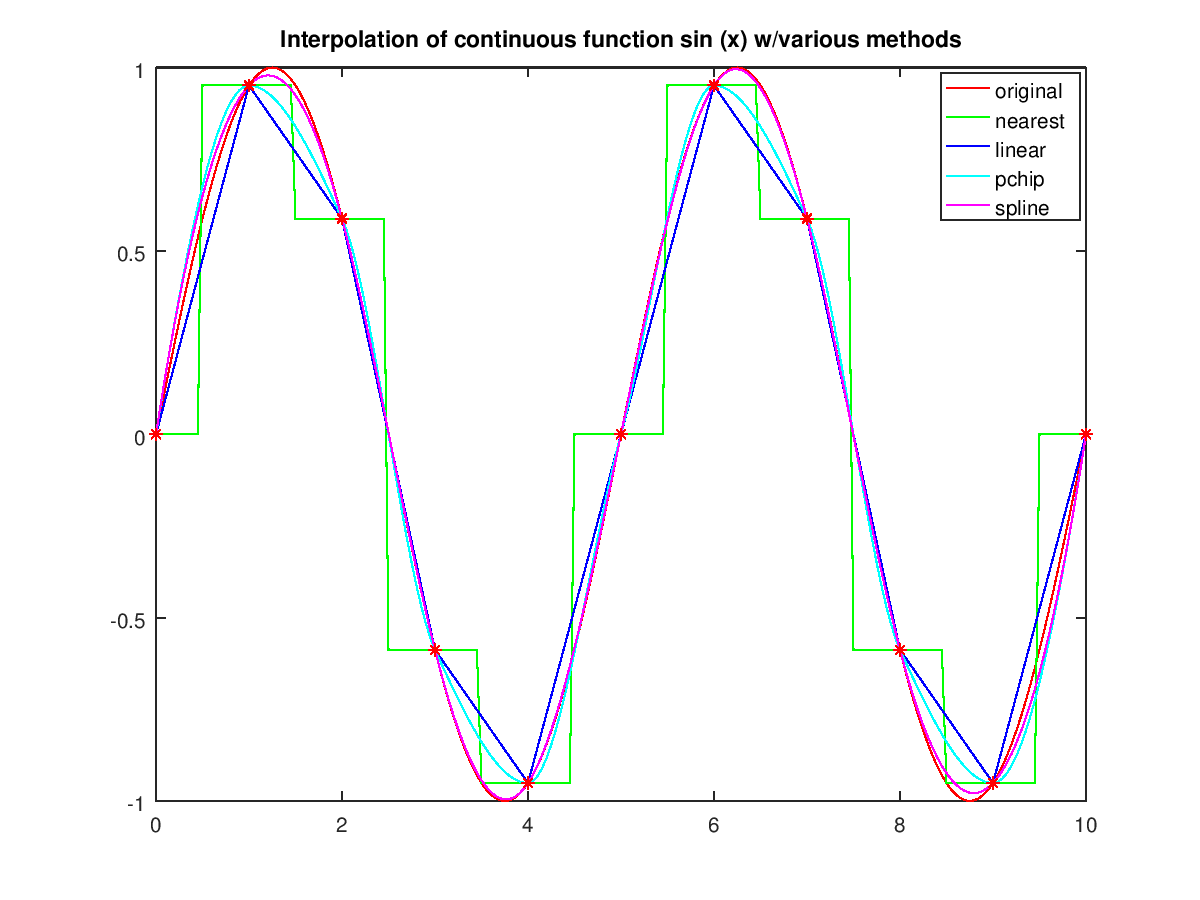
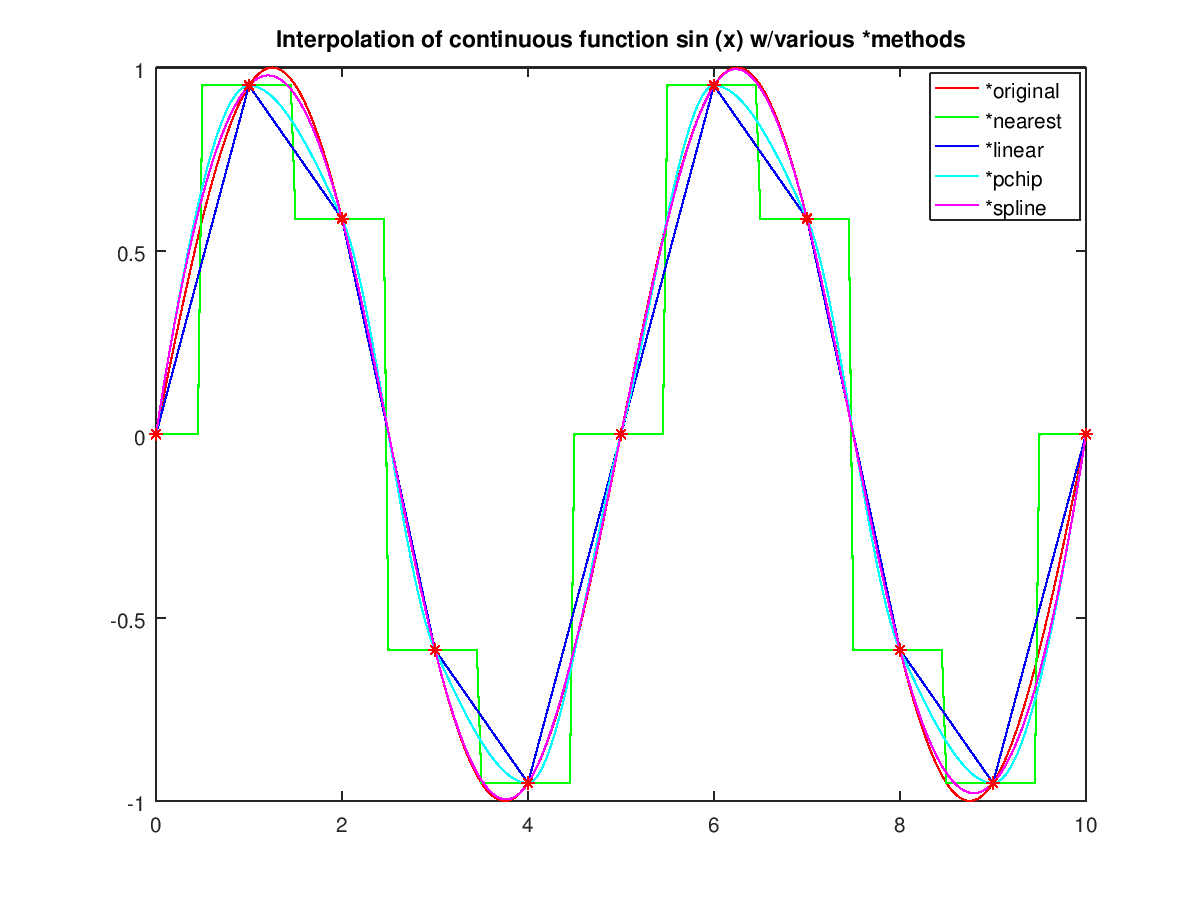
The following code

 clf;
 xf = 0:0.05:10;  yf = sin (2*pi*xf/5);
 xp = 0:10;       yp = sin (2*pi*xp/5);
 lin = interp1 (xp,yp,xf, 'linear');
 spl = interp1 (xp,yp,xf, 'spline');
 pch = interp1 (xp,yp,xf, 'pchip');
 near= interp1 (xp,yp,xf, 'nearest');
 plot (xf,yf,'r',xf,near,'g',xf,lin,'b',xf,pch,'c',xf,spl,'m',xp,yp,'r*');
 legend ('original', 'nearest', 'linear', 'pchip', 'spline');
 title ('Interpolation of continuous function sin (x) w/various methods');
 %--------------------------------------------------------
 % confirm that interpolated function matches the original

Produces the following figure

Figure 1

Demonstration 2

The following code

 clf;
 xf = 0:0.05:10;  yf = sin (2*pi*xf/5);
 xp = 0:10;       yp = sin (2*pi*xp/5);
 lin = interp1 (xp,yp,xf, '*linear');
 spl = interp1 (xp,yp,xf, '*spline');
 pch = interp1 (xp,yp,xf, '*pchip');
 near= interp1 (xp,yp,xf, '*nearest');
 plot (xf,yf,'r',xf,near,'g',xf,lin,'b',xf,pch,'c',xf,spl,'m',xp,yp,'r*');
 legend ('*original', '*nearest', '*linear', '*pchip', '*spline');
 title ('Interpolation of continuous function sin (x) w/various *methods');
 %--------------------------------------------------------
 % confirm that interpolated function matches the original

Produces the following figure

Figure 1

Demonstration 3

The following code

 clf;
 fstep = @(x) x > 1;
 xf = 0:0.05:2;  yf = fstep (xf);
 xp = linspace (0,2,10);  yp = fstep (xp);
 pch = interp1 (xp,yp,xf, 'pchip');
 spl = interp1 (xp,yp,xf, 'spline');
 plot (xf,yf,'r',xf,pch,'b',xf,spl,'m',xp,yp,'r*');
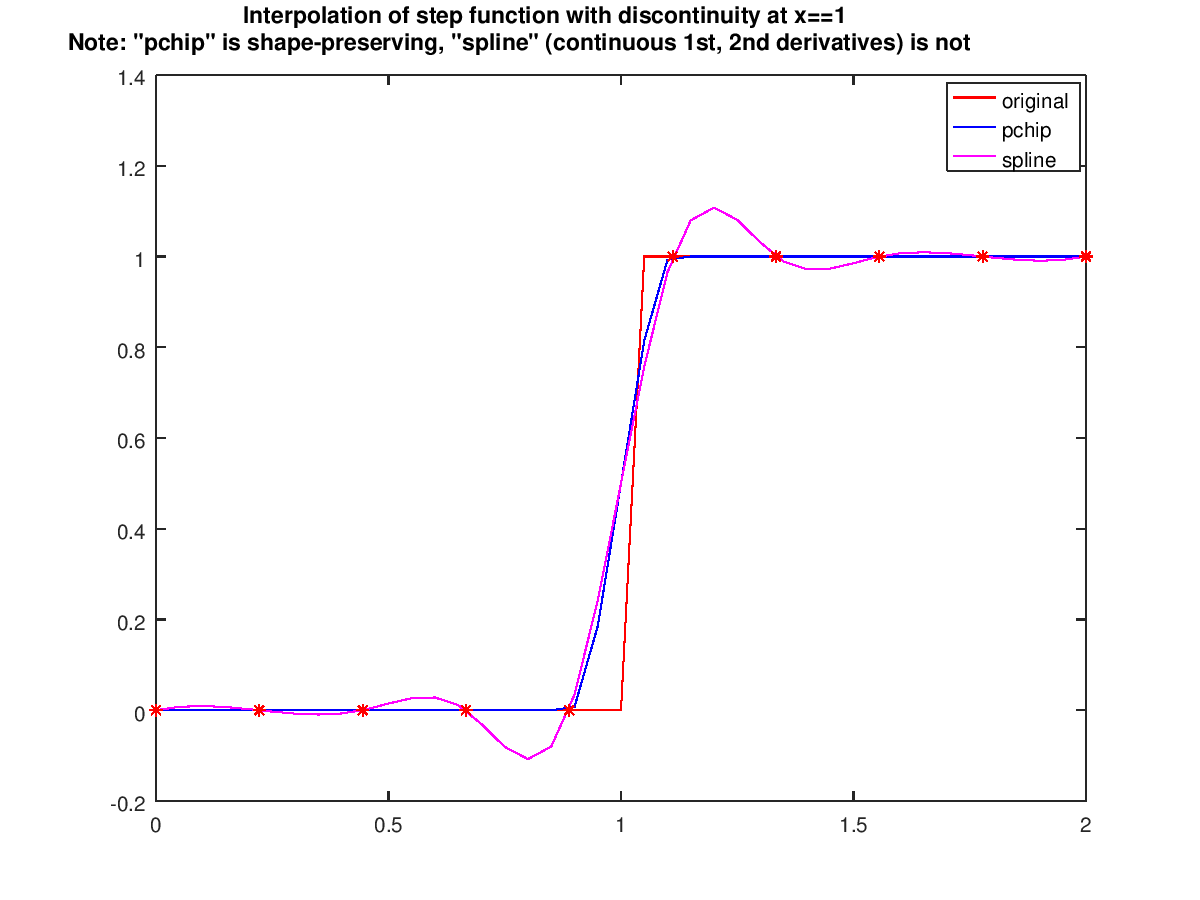
 title ({'Interpolation of step function with discontinuity at x==1', ...
         'Note: "pchip" is shape-preserving, "spline" (continuous 1st, 2nd derivatives) is not'});
 legend ('original', 'pchip', 'spline');

Produces the following figure

Figure 1

Demonstration 4

The following code

 clf;
 t = 0 : 0.3 : pi; dt = t(2)-t(1);
 n = length (t); k = 100; dti = dt*n/k;
 ti = t(1) + [0 : k-1]*dti;
 y = sin (4*t + 0.3) .* cos (3*t - 0.1);
 ddys = diff (diff (interp1 (t,y,ti, 'spline'))./dti)./dti;
 ddyp = diff (diff (interp1 (t,y,ti, 'pchip')) ./dti)./dti;
 ddyc = diff (diff (interp1 (t,y,ti, 'cubic')) ./dti)./dti;
 plot (ti(2:end-1),ddys,'b*', ti(2:end-1),ddyp,'c^', ti(2:end-1),ddyc,'g+');
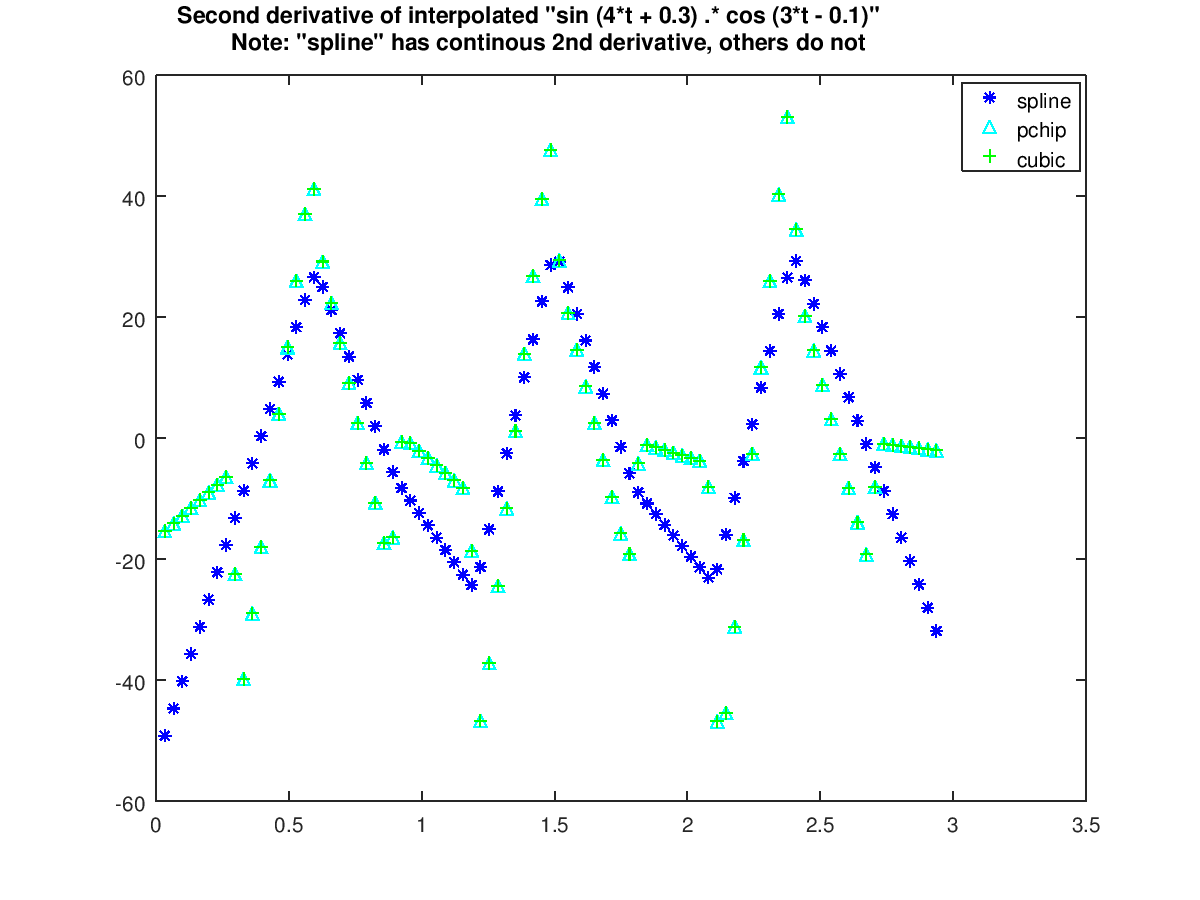
 title ({'Second derivative of interpolated "sin (4*t + 0.3) .* cos (3*t - 0.1)"', ...
         'Note: "spline" has continous 2nd derivative, others do not'});
 legend ('spline', 'pchip', 'cubic');

Produces the following figure

Figure 1

Demonstration 5

The following code

 clf;
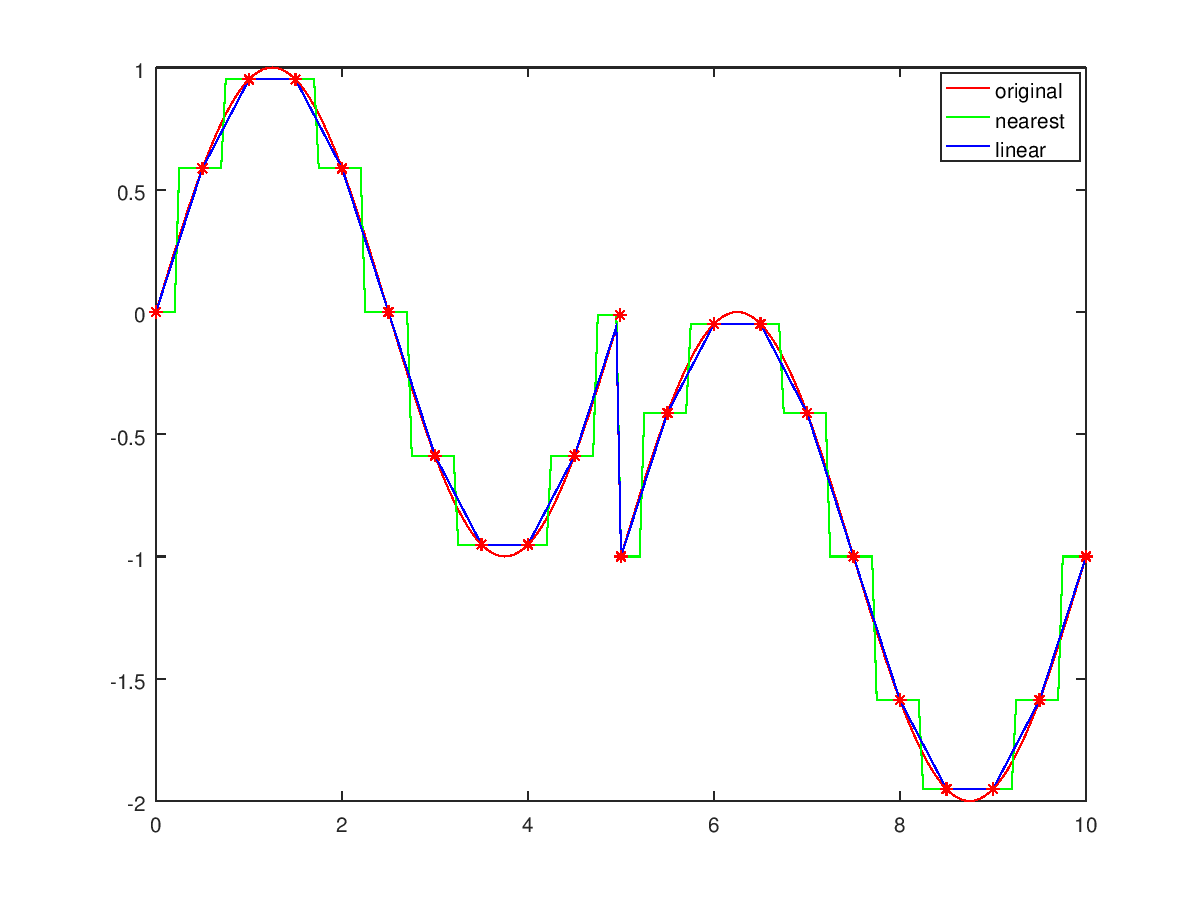
 xf = 0:0.05:10;                yf = sin (2*pi*xf/5) - (xf >= 5);
 xp = [0:.5:4.5,4.99,5:.5:10];  yp = sin (2*pi*xp/5) - (xp >= 5);
 lin = interp1 (xp,yp,xf, 'linear');
 near= interp1 (xp,yp,xf, 'nearest');
 plot (xf,yf,'r', xf,near,'g', xf,lin,'b', xp,yp,'r*');
 legend ('original', 'nearest', 'linear');
 %--------------------------------------------------------
 % confirm that interpolated function matches the original

Produces the following figure

Figure 1

Demonstration 6

The following code

 clf;
 x = 0:0.5:3;
 x1 = [3 2 2 1];
 x2 = [1 2 2 3];
 y1 = [1 1 0 0];
 y2 = [0 0 1 1];
 h = plot (x, interp1 (x1, y1, x), 'b', x1, y1, 'sb');
 hold on
 g = plot (x, interp1 (x2, y2, x), 'r', x2, y2, '*r');
 axis ([0.5 3.5 -0.5 1.5]);
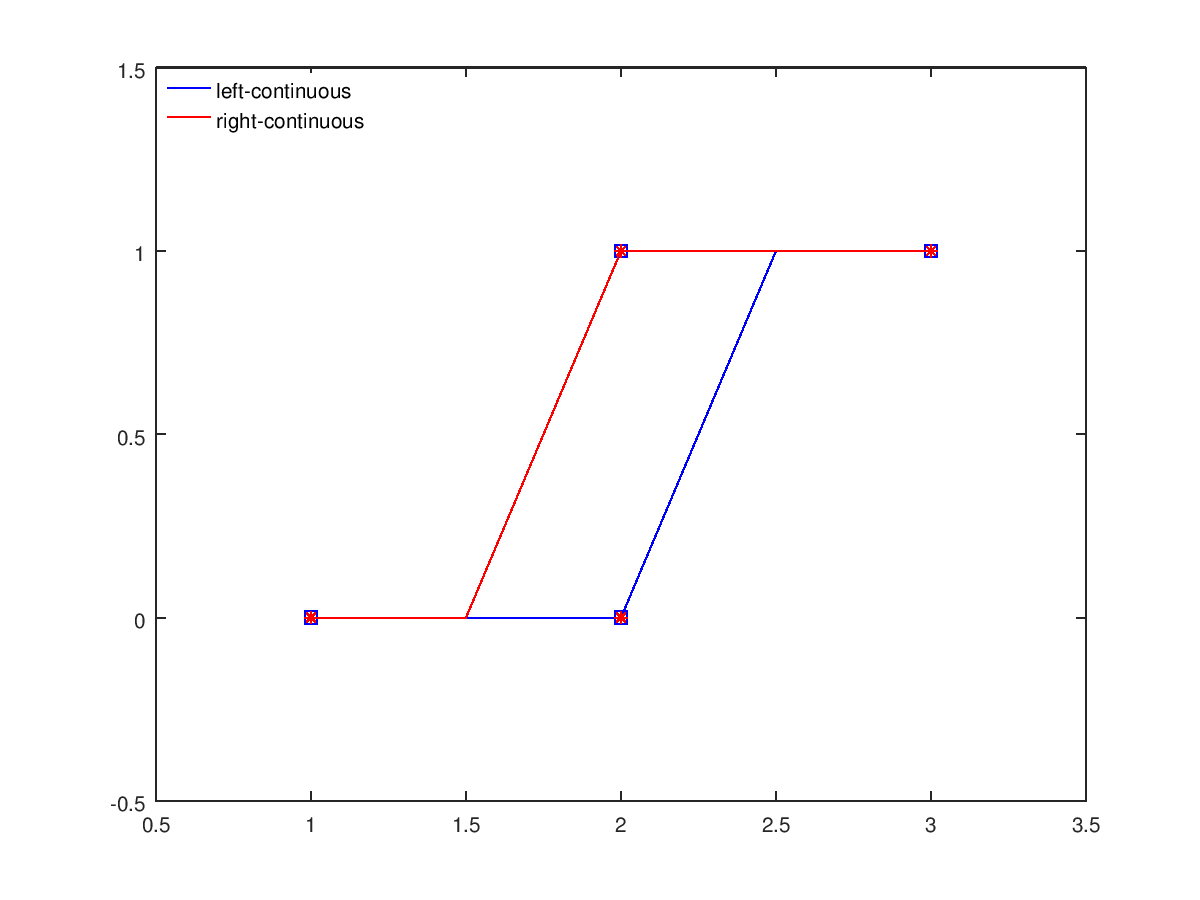
 legend ([h(1), g(1)], {'left-continuous', 'right-continuous'}, ...
         'location', 'northwest')
 legend boxoff
 %--------------------------------------------------------
 % red curve is left-continuous and blue is right-continuous at x = 2

Produces the following figure

Figure 1

Package: octave