Navigation

Operators and Keywords

Function List:

C++ API

: pp = mkpp (breaks, coefs)
: pp = mkpp (breaks, coefs, d)

Construct a piecewise polynomial (pp) structure from sample points breaks and coefficients coefs.

breaks must be a vector of strictly increasing values. The number of intervals is given by ni = length (breaks) - 1.

When m is the polynomial order coefs must be of size: ni x m + 1.

The i-th row of coefs, coefs (i,:), contains the coefficients for the polynomial over the i-th interval, ordered from highest (m) to lowest (0).

coefs may also be a multi-dimensional array, specifying a vector-valued or array-valued polynomial. In that case the polynomial order is defined by the length of the last dimension of coefs. The size of first dimension(s) are given by the scalar or vector d. If d is not given it is set to 1. In any case coefs is reshaped to a 2-D matrix of size [ni*prod(d m)].

See also: unmkpp, ppval, spline, pchip, ppder, ppint, ppjumps.

Demonstration 1

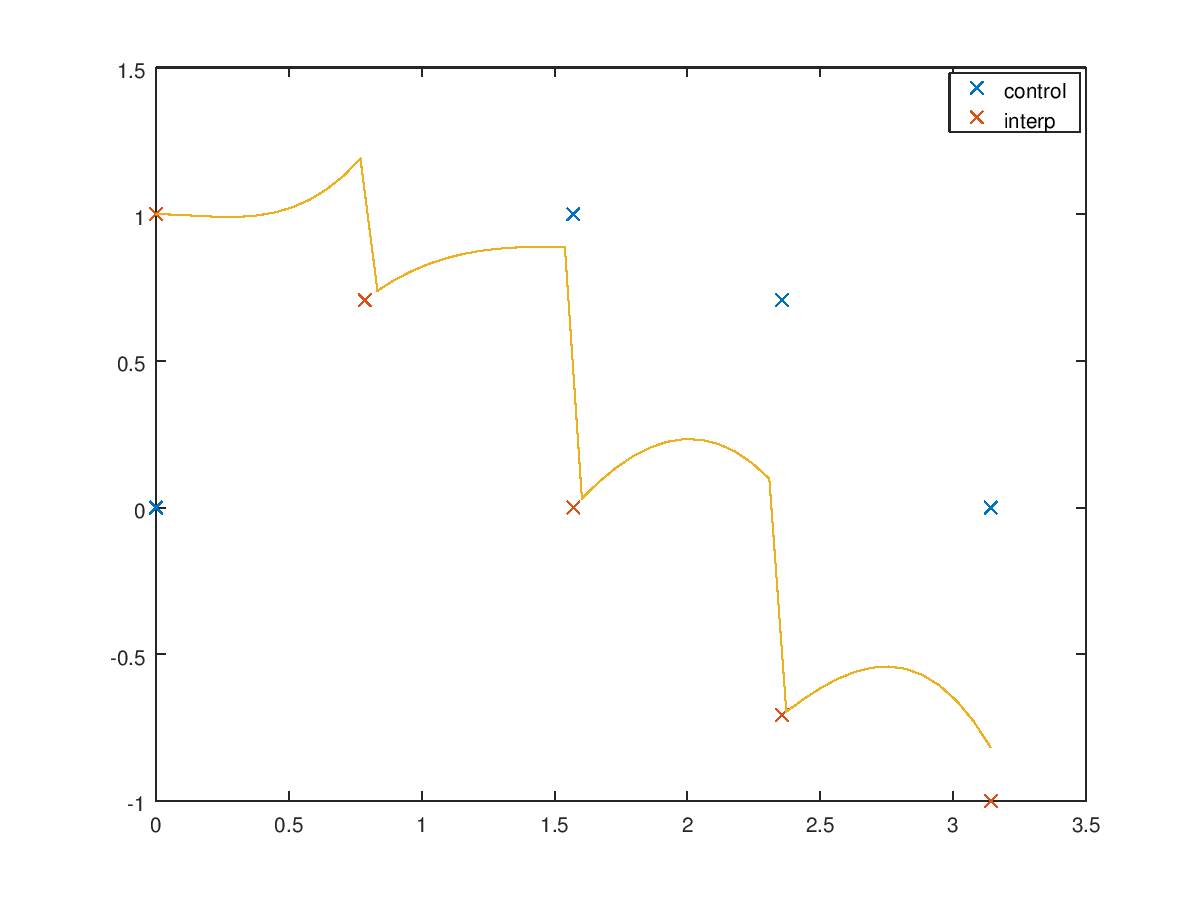
The following code

 # linear interpolation
 x = linspace (0,pi,5)';
 t = [sin(x), cos(x)];
 m = diff (t) ./ (x(2)-x(1));
 b = t(1:4,:);
 pp = mkpp (x, [m(:),b(:)]);
 xi = linspace (0,pi,50);
 plot (x,t,"x", xi,ppval (pp,xi));
 legend ("control", "interp");

Produces the following figure

Figure 1

Package: octave