Navigation

Operators and Keywords

Function List:

C++ API

: x = pcg (A, b, tol, maxit, m1, m2, x0, …)
: [x, flag, relres, iter, resvec, eigest] = pcg (…)

Solve the linear system of equations A * x = b by means of the Preconditioned Conjugate Gradient iterative method.

The input arguments are

  • A can be either a square (preferably sparse) matrix or a function handle, inline function or string containing the name of a function which computes A * x. In principle, A should be symmetric and positive definite; if pcg finds A not to be positive definite, a warning is printed and the flag output will be set.
  • b is the right-hand side vector.
  • tol is the required relative tolerance for the residual error, b - A * x. The iteration stops if norm (b - A * x) ≤ tol * norm (b). If tol is omitted or empty then a tolerance of 1e-6 is used.
  • maxit is the maximum allowable number of iterations; if maxit is omitted or empty then a value of 20 is used.
  • m = m1 * m2 is the (left) preconditioning matrix, so that the iteration is (theoretically) equivalent to solving by pcg P * x = m \ b, with P = m \ A. Note that a proper choice of the preconditioner may dramatically improve the overall performance of the method. Instead of matrices m1 and m2, the user may pass two functions which return the results of applying the inverse of m1 and m2 to a vector (usually this is the preferred way of using the preconditioner). If m1 is omitted or empty [] then no preconditioning is applied. If m2 is omitted, m = m1 will be used as a preconditioner.
  • x0 is the initial guess. If x0 is omitted or empty then the function sets x0 to a zero vector by default.

The arguments which follow x0 are treated as parameters, and passed in a proper way to any of the functions (A or m) which are passed to pcg. See the examples below for further details. The output arguments are

  • x is the computed approximation to the solution of A * x = b.
  • flag reports on the convergence. A value of 0 means the solution converged and the tolerance criterion given by tol is satisfied. A value of 1 means that the maxit limit for the iteration count was reached. A value of 3 indicates that the (preconditioned) matrix was found not to be positive definite.
  • relres is the ratio of the final residual to its initial value, measured in the Euclidean norm.
  • iter is the actual number of iterations performed.
  • resvec describes the convergence history of the method. resvec(i,1) is the Euclidean norm of the residual, and resvec(i,2) is the preconditioned residual norm, after the (i-1)-th iteration, i = 1, 2, …, iter+1. The preconditioned residual norm is defined as norm (r) ^ 2 = r' * (m \ r) where r = b - A * x, see also the description of m. If eigest is not required, only resvec(:,1) is returned.
  • eigest returns the estimate for the smallest eigest(1) and largest eigest(2) eigenvalues of the preconditioned matrix P = m \ A. In particular, if no preconditioning is used, the estimates for the extreme eigenvalues of A are returned. eigest(1) is an overestimate and eigest(2) is an underestimate, so that eigest(2) / eigest(1) is a lower bound for cond (P, 2), which nevertheless in the limit should theoretically be equal to the actual value of the condition number. The method which computes eigest works only for symmetric positive definite A and m, and the user is responsible for verifying this assumption.

Let us consider a trivial problem with a diagonal matrix (we exploit the sparsity of A) 

n = 10;
A = diag (sparse (1:n));
b = rand (n, 1);
[l, u, p] = ilu (A, struct ("droptol", 1.e-3));

EXAMPLE 1: Simplest use of pcg 

x = pcg (A, b)

EXAMPLE 2: pcg with a function which computes A * x 

function y = apply_a (x)
  y = [1:N]' .* x;
endfunction

x = pcg ("apply_a", b)

EXAMPLE 3: pcg with a preconditioner: l * u 

x = pcg (A, b, 1.e-6, 500, l*u)

EXAMPLE 4: pcg with a preconditioner: l * u. Faster than EXAMPLE 3 since lower and upper triangular matrices are easier to invert 

x = pcg (A, b, 1.e-6, 500, l, u)

EXAMPLE 5: Preconditioned iteration, with full diagnostics. The preconditioner (quite strange, because even the original matrix A is trivial) is defined as a function 

function y = apply_m (x)
  k = floor (length (x) - 2);
  y = x;
  y(1:k) = x(1:k) ./ [1:k]';
endfunction

[x, flag, relres, iter, resvec, eigest] = ...
                   pcg (A, b, [], [], "apply_m");
semilogy (1:iter+1, resvec);

EXAMPLE 6: Finally, a preconditioner which depends on a parameter k. 

function y = apply_M (x, varargin)
  K = varargin{1};
  y = x;
  y(1:K) = x(1:K) ./ [1:K]';
endfunction

[x, flag, relres, iter, resvec, eigest] = ...
     pcg (A, b, [], [], "apply_m", [], [], 3)

References:

  1. C.T. Kelley, Iterative Methods for Linear and Nonlinear Equations, SIAM, 1995. (the base PCG algorithm)
  2. Y. Saad, Iterative Methods for Sparse Linear Systems, PWS 1996. (condition number estimate from PCG) Revised version of this book is available online at http://www-users.cs.umn.edu/~saad/books.html

See also: sparse, pcr.

Demonstration 1

The following code

 ## Simplest usage of pcg (see also 'help pcg')

 N = 10;
 A = diag ([1:N]); b = rand (N, 1);
 y = A \ b;  # y is the true solution
 x = pcg (A, b);
 printf ("The solution relative error is %g\n", norm (x - y) / norm (y));

 ## You shouldn't be afraid if pcg issues some warning messages in this
 ## example: watch out in the second example, why it takes N iterations
 ## of pcg to converge to (a very accurate, by the way) solution

Produces the following output

warning: pcg: maximum number of iterations (10) reached
warning: pcg: the initial residual norm was reduced 3.31952e+17 times.
The solution relative error is 1.23135e-16

Demonstration 2

The following code

 ## Full output from pcg, except for the eigenvalue estimates
 ## We use this output to plot the convergence history

 N = 10;
 A = diag ([1:N]); b = rand (N, 1);
 X = A \ b;  # X is the true solution
 [x, flag, relres, iter, resvec] = pcg (A, b);
 printf ("The solution relative error is %g\n", norm (x - X) / norm (X));
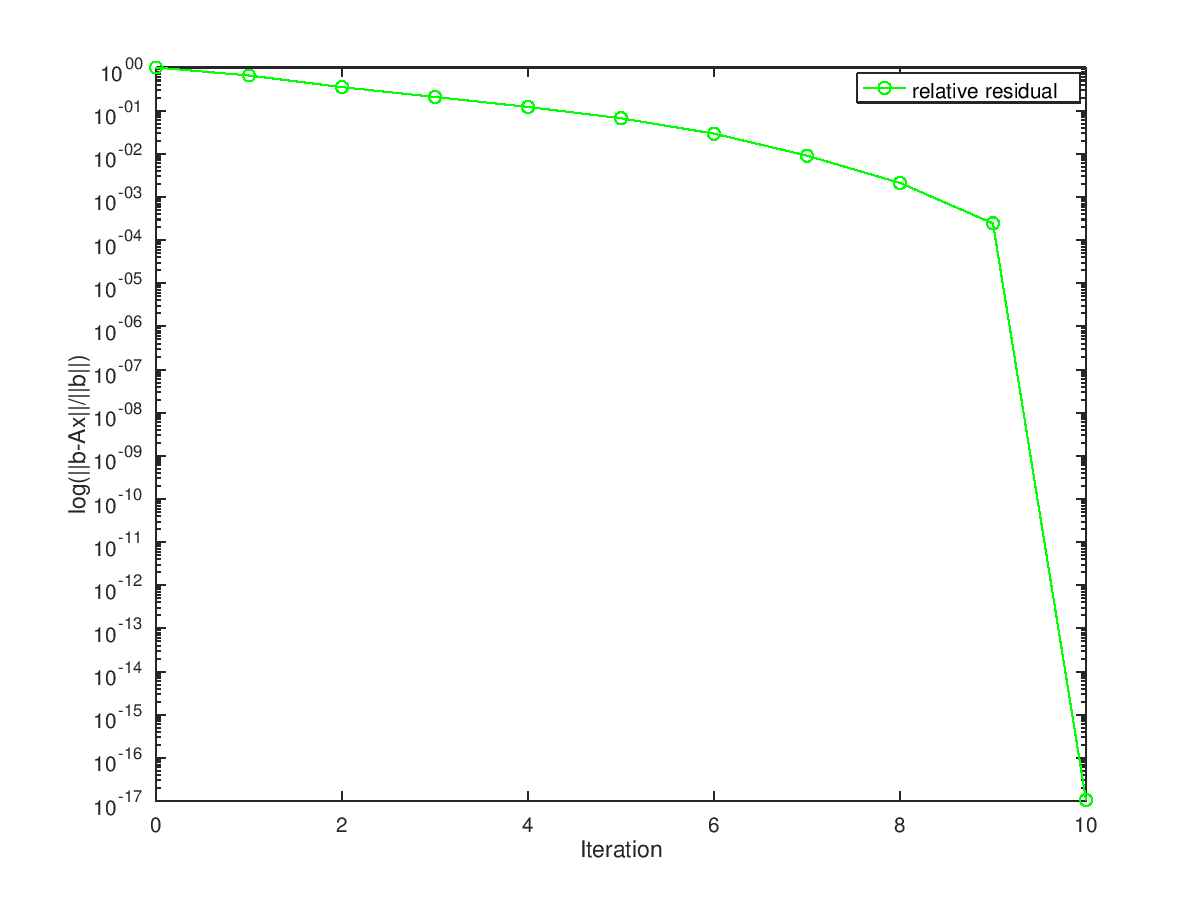
 title ("Convergence history");
 semilogy ([0:iter], resvec / resvec(1), "o-g");
 xlabel ("Iteration"); ylabel ("log(||b-Ax||/||b||)");
 legend ("relative residual");

Produces the following output

The solution relative error is 1.98722e-16

and the following figure

Figure 1

Demonstration 3

The following code

 ## Full output from pcg, including the eigenvalue estimates
 ## Hilbert matrix is extremely ill-conditioned, so pcg WILL have problems

 N = 10;
 A = hilb (N); b = rand (N, 1);
 X = A \ b;  # X is the true solution
 [x, flag, relres, iter, resvec, eigest] = pcg (A, b, [], 200);
 printf ("The solution relative error is %g\n", norm (x - X) / norm (X));
 printf ("Condition number estimate is %g\n", eigest(2) / eigest(1));
 printf ("Actual condition number is   %g\n", cond (A));
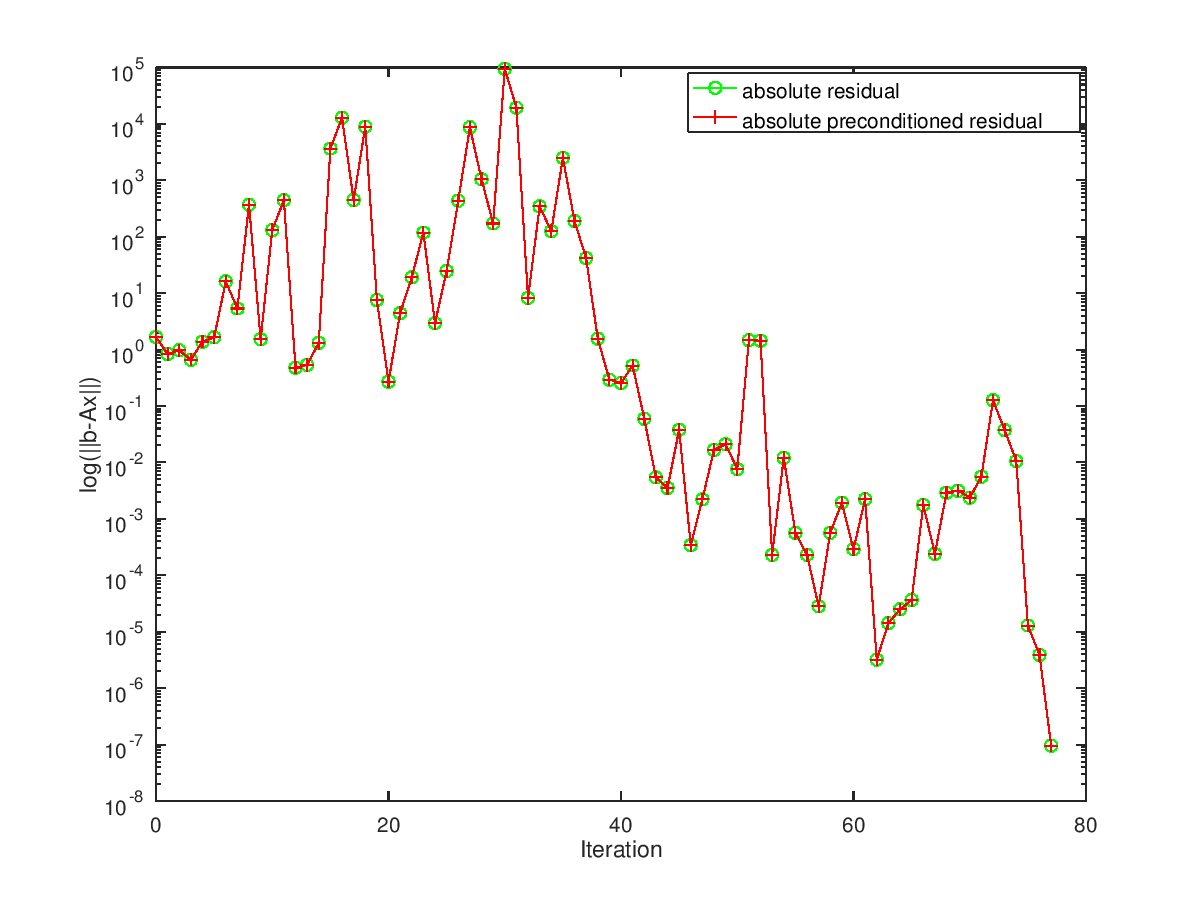
 title ("Convergence history");
 semilogy ([0:iter], resvec, ["o-g";"+-r"]);
 xlabel ("Iteration"); ylabel ("log(||b-Ax||)");
 legend ("absolute residual", "absolute preconditioned residual");

Produces the following output

The solution relative error is 0.000123006
Condition number estimate is 1.60432e+13
Actual condition number is   1.60244e+13

and the following figure

Figure 1

Demonstration 4

The following code

 ## Full output from pcg, including the eigenvalue estimates
 ## We use the 1-D Laplacian matrix for A, and cond(A) = O(N^2)
 ## and that's the reason we need some preconditioner; here we take
 ## a very simple and not powerful Jacobi preconditioner,
 ## which is the diagonal of A.

 N = 100;
 A = zeros (N, N);
 for i = 1 : N - 1 # form 1-D Laplacian matrix
   A(i:i+1, i:i+1) = [2 -1; -1 2];
 endfor
 b = rand (N, 1);
 X = A \ b;  # X is the true solution
 maxit = 80;
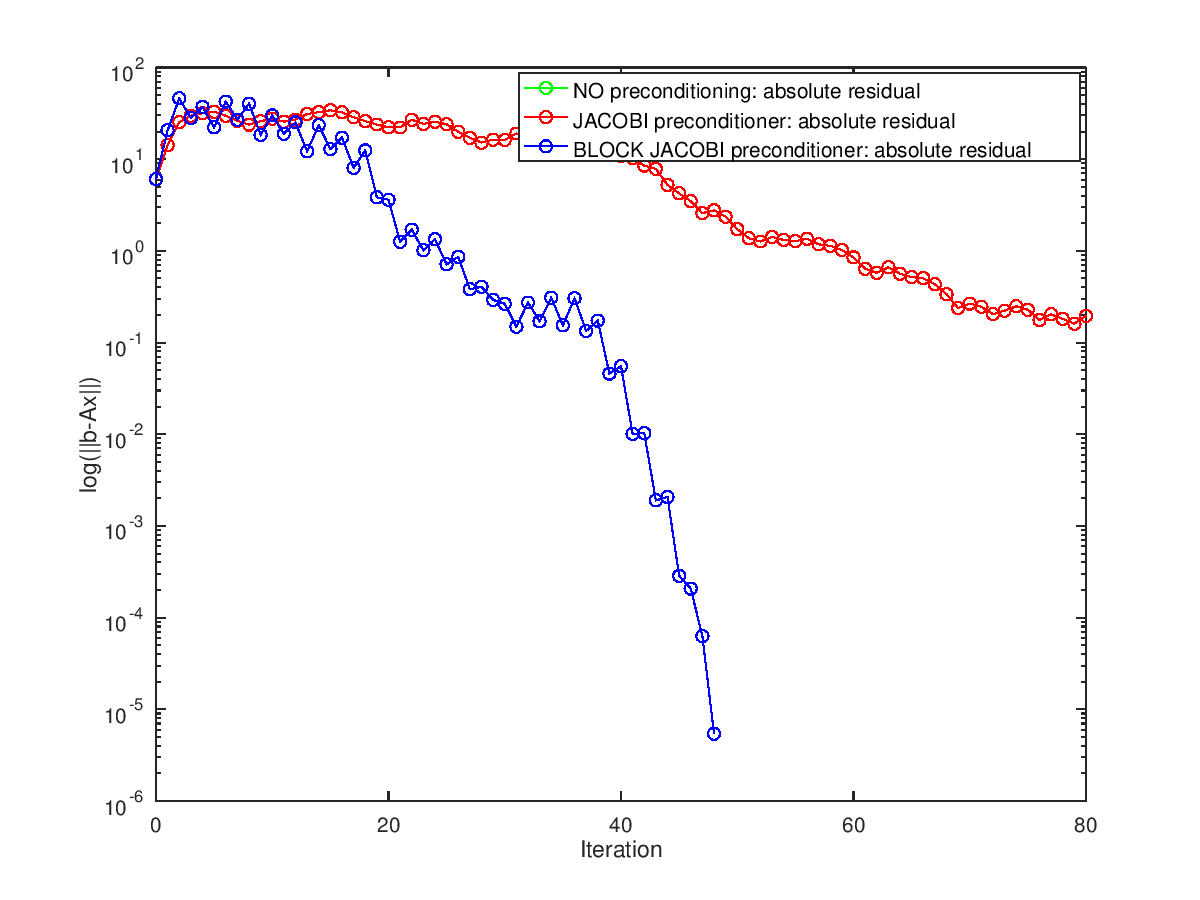
 printf ("System condition number is %g\n", cond (A));
 ## No preconditioner: the convergence is very slow!

 [x, flag, relres, iter, resvec, eigest] = pcg (A, b, [], maxit);
 printf ("System condition number estimate is %g\n", eigest(2) / eigest(1));
 title ("Convergence history");
 semilogy ([0:iter], resvec(:,1), "o-g");
 xlabel ("Iteration"); ylabel ("log(||b-Ax||)");
 legend ("NO preconditioning: absolute residual");

 pause (1);
 ## Test Jacobi preconditioner: it will not help much!!!

 M = diag (diag (A)); # Jacobi preconditioner
 [x, flag, relres, iter, resvec, eigest] = pcg (A, b, [], maxit, M);
 printf ("JACOBI preconditioned system condition number estimate is %g\n", eigest(2) / eigest(1));
 hold on;
 semilogy ([0:iter], resvec(:,1), "o-r");
 legend ("NO preconditioning: absolute residual", ...
         "JACOBI preconditioner: absolute residual");

 pause (1);
 ## Test nonoverlapping block Jacobi preconditioner: it will help much!

 M = zeros (N, N); k = 4;
 for i = 1 : k : N # form 1-D Laplacian matrix
   M(i:i+k-1, i:i+k-1) = A(i:i+k-1, i:i+k-1);
 endfor
 [x, flag, relres, iter, resvec, eigest] = pcg (A, b, [], maxit, M);
 printf ("BLOCK JACOBI preconditioned system condition number estimate is %g\n", eigest(2) / eigest(1));
 semilogy ([0:iter], resvec(:,1), "o-b");
 legend ("NO preconditioning: absolute residual", ...
         "JACOBI preconditioner: absolute residual", ...
         "BLOCK JACOBI preconditioner: absolute residual");
 hold off;

Produces the following output

System condition number is 4133.64
System condition number estimate is 4133.21
JACOBI preconditioned system condition number estimate is 4133.21
BLOCK JACOBI preconditioned system condition number estimate is 1034.61

and the following figure

Figure 1

Package: octave