Function Reference: pcr

: x = pcr (A, b, tol, maxit, m, x0, …)

: [x, flag, relres, iter, resvec] = pcr (…)

Solve the linear system of equations A * x = b by means of the Preconditioned Conjugate Residuals iterative method.

The input arguments are

A can be either a square (preferably sparse) matrix or a function handle, inline function or string containing the name of a function which computes A * x. In principle A should be symmetric and non-singular; if pcr finds A to be numerically singular, you will get a warning message and the flag output parameter will be set.
b is the right hand side vector.
tol is the required relative tolerance for the residual error, b - A * x. The iteration stops if norm (b - A * x) <= tol * norm (b - A * x0). If tol is empty or is omitted, the function sets tol = 1e-6 by default.
maxit is the maximum allowable number of iterations; if [] is supplied for maxit, or pcr has less arguments, a default value equal to 20 is used.
m is the (left) preconditioning matrix, so that the iteration is (theoretically) equivalent to solving by pcr P * x = m \ b, with P = m \ A. Note that a proper choice of the preconditioner may dramatically improve the overall performance of the method. Instead of matrix m, the user may pass a function which returns the results of applying the inverse of m to a vector (usually this is the preferred way of using the preconditioner). If [] is supplied for m, or m is omitted, no preconditioning is applied.
x0 is the initial guess. If x0 is empty or omitted, the function sets x0 to a zero vector by default.

The arguments which follow x0 are treated as parameters, and passed in a proper way to any of the functions (A or m) which are passed to pcr. See the examples below for further details.

The output arguments are

x is the computed approximation to the solution of A * x = b.
flag reports on the convergence. flag = 0 means the solution converged and the tolerance criterion given by tol is satisfied. flag = 1 means that the maxit limit for the iteration count was reached. flag = 3 reports a pcr breakdown, see [1] for details.
relres is the ratio of the final residual to its initial value, measured in the Euclidean norm.
iter is the actual number of iterations performed.
resvec describes the convergence history of the method, so that resvec (i) contains the Euclidean norms of the residual after the (i-1)-th iteration, i = 1,2, …, iter+1.

Let us consider a trivial problem with a diagonal matrix (we exploit the sparsity of A)

n = 10;
A = sparse (diag (1:n));
b = rand (N, 1);

EXAMPLE 1: Simplest use of pcr

x = pcr (A, b)

EXAMPLE 2: pcr with a function which computes A * x.

function y = apply_a (x)
  y = [1:10]' .* x;
endfunction

x = pcr ("apply_a", b)

EXAMPLE 3: Preconditioned iteration, with full diagnostics. The preconditioner (quite strange, because even the original matrix A is trivial) is defined as a function

function y = apply_m (x)
  k = floor (length (x) - 2);
  y = x;
  y(1:k) = x(1:k) ./ [1:k]';
endfunction

[x, flag, relres, iter, resvec] = ...
                   pcr (A, b, [], [], "apply_m")
semilogy ([1:iter+1], resvec);

EXAMPLE 4: Finally, a preconditioner which depends on a parameter k.

function y = apply_m (x, varargin)
  k = varargin{1};
  y = x;
  y(1:k) = x(1:k) ./ [1:k]';
endfunction

[x, flag, relres, iter, resvec] = ...
                   pcr (A, b, [], [], "apply_m"', [], 3)

References:

[1] W. Hackbusch, Iterative Solution of Large Sparse Systems of Equations, section 9.5.4; Springer, 1994

See also: sparse, pcg.

Demonstration 1

The following code

 ## Simplest usage of PCR (see also 'help pcr')

 N = 20;
 A = diag (linspace (-3.1,3,N)); b = rand (N,1);
 y = A \ b;  # y is the true solution
 x = pcr (A,b);
 printf ("The solution relative error is %g\n", norm (x-y) / norm (y));

 ## You shouldn't be afraid if PCR issues some warning messages in this
 ## example: watch out in the second example, why it takes N iterations
 ## of PCR to converge to (a very accurate, by the way) solution.

Produces the following output

warning: pcr: maximum number of iterations (20) reached
warning: pcr: the initial residual norm was reduced 1.75488e+10 times
The solution relative error is 2.1769e-11

Demonstration 2

The following code

 ## Full output from PCR
 ## We use this output to plot the convergence history

 N = 20;
 A = diag (linspace (-3.1,30,N)); b = rand (N,1);
 X = A \ b;  # X is the true solution
 [x, flag, relres, iter, resvec] = pcr (A,b);
 printf ("The solution relative error is %g\n", norm (x-X) / norm (X));
 clf;
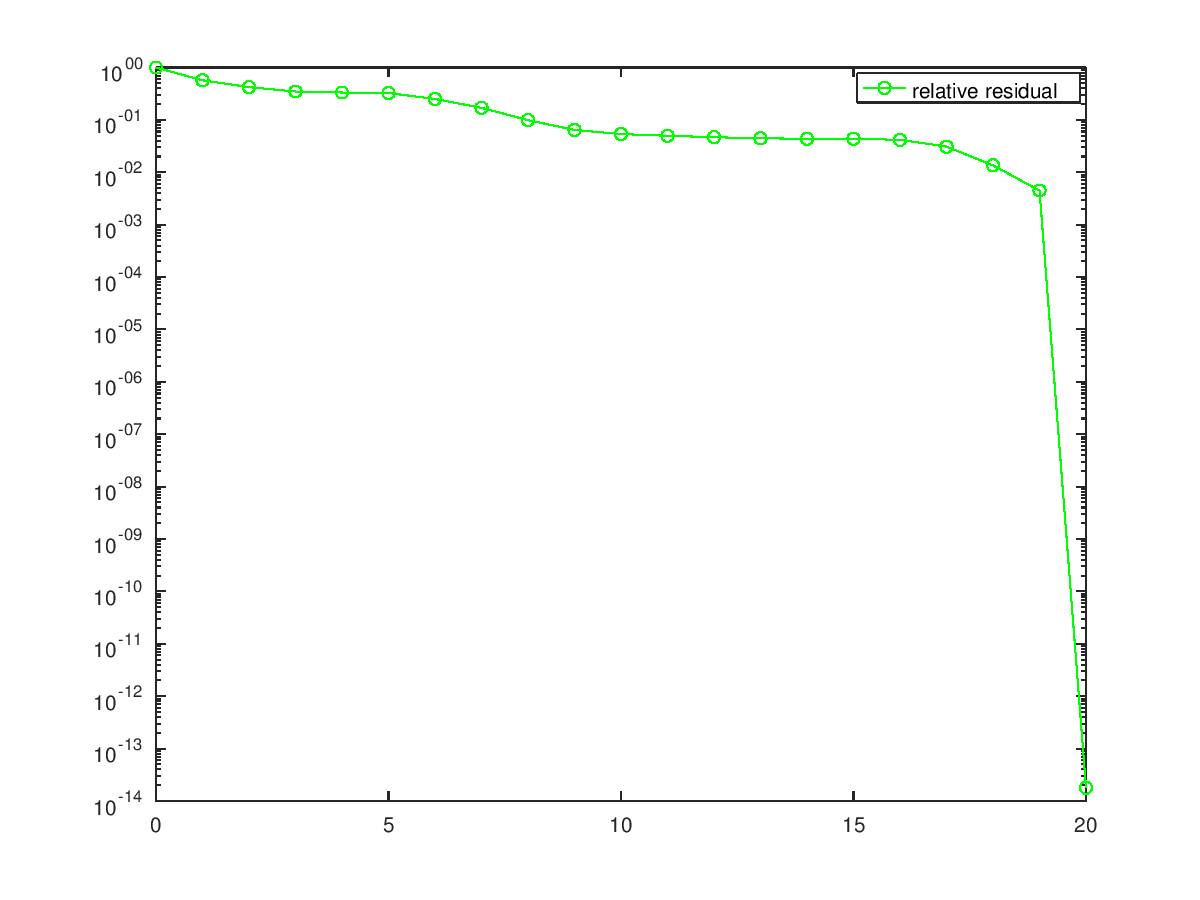
 title ("Convergence history");
 xlabel ("Iteration"); ylabel ("log(||b-Ax||/||b||)");
 semilogy ([0:iter], resvec/resvec(1), "o-g;relative residual;");

Produces the following output

The solution relative error is 5.17225e-15

and the following figure

Figure 1

Demonstration 3

The following code

 ## Full output from PCR
 ## We use indefinite matrix based on the Hilbert matrix, with one
 ## strongly negative eigenvalue
 ## Hilbert matrix is extremely ill conditioned, so is ours,
 ## and that's why PCR WILL have problems

 N = 10;
 A = hilb (N); A(1,1) = -A(1,1); b = rand (N,1);
 X = A \ b;  # X is the true solution
 printf ("Condition number of A is   %g\n", cond (A));
 [x, flag, relres, iter, resvec] = pcr (A,b,[],200);
 if (flag == 3)
   printf ("PCR breakdown.  System matrix is [close to] singular\n");
 endif
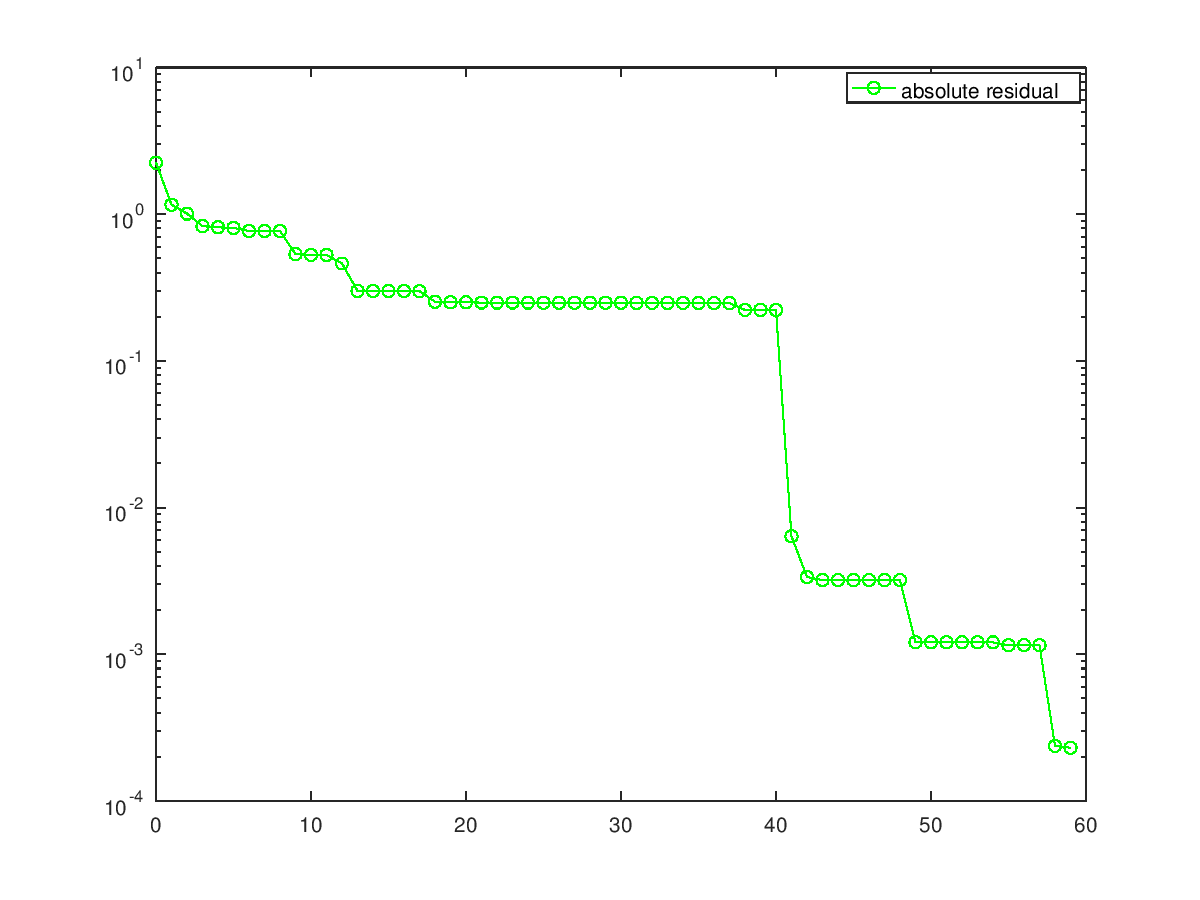
 clf;
 title ("Convergence history");
 xlabel ("Iteration"); ylabel ("log(||b-Ax||)");
 semilogy ([0:iter], resvec, "o-g;absolute residual;");

Produces the following output

Condition number of A is   8.64595e+12
PCR breakdown.  System matrix is [close to] singular

and the following figure

Figure 1

Demonstration 4

The following code

 ## Full output from PCR
 ## We use an indefinite matrix based on the 1-D Laplacian matrix for A,
 ## and here we have cond(A) = O(N^2)
 ## That's the reason we need some preconditioner; here we take
 ## a very simple and not powerful Jacobi preconditioner,
 ## which is the diagonal of A.

 ## Note that we use here indefinite preconditioners!

 N = 100;
 A = zeros (N,N);
 for i=1:N-1 # form 1-D Laplacian matrix
   A(i:i+1,i:i+1) = [2 -1; -1 2];
 endfor
 A = [A, zeros(size(A)); zeros(size(A)), -A];
 b = rand (2*N,1);
 X = A \ b;  # X is the true solution
 maxit = 80;
 printf ("System condition number is %g\n", cond (A));
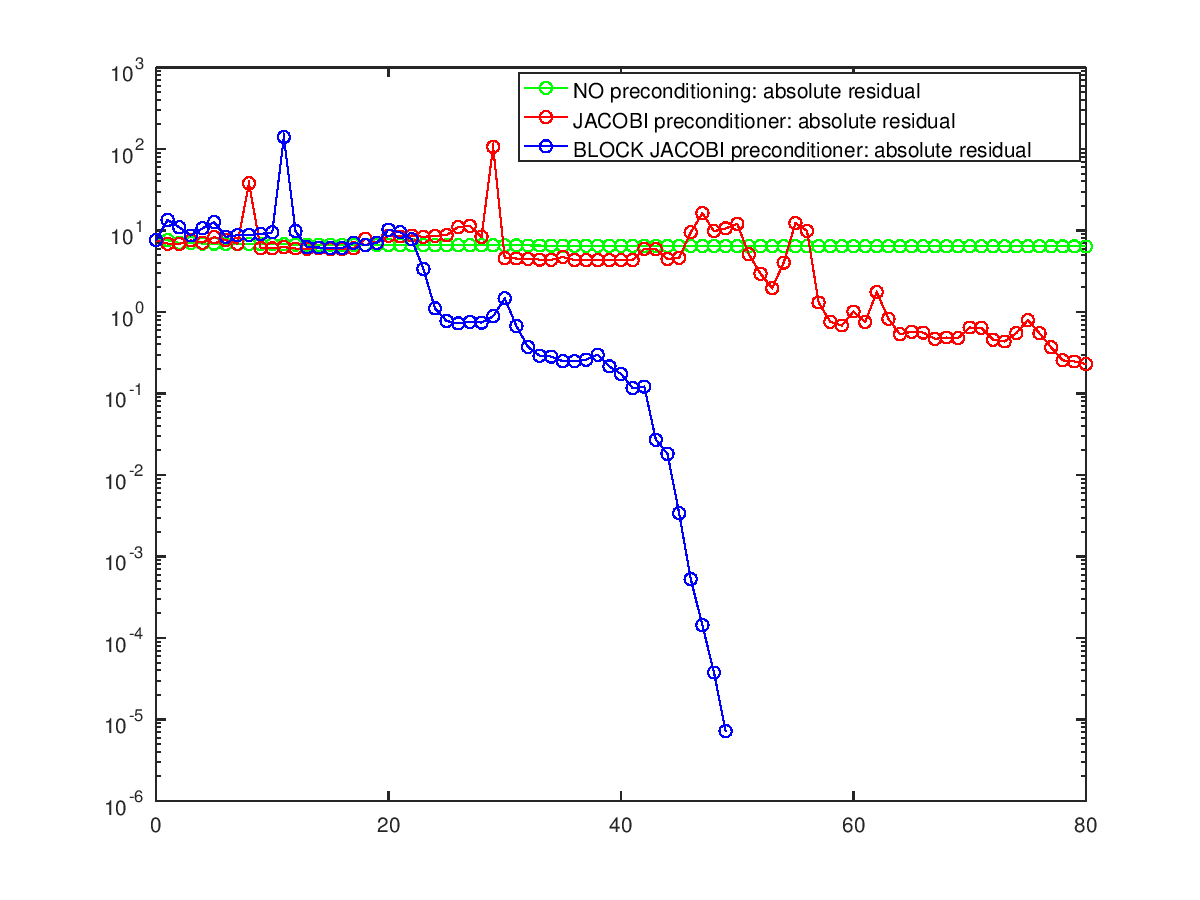
 ## No preconditioner: the convergence is very slow!

 [x, flag, relres, iter, resvec] = pcr (A,b,[],maxit);
 clf;
 title ("Convergence history");
 xlabel ("Iteration"); ylabel ("log(||b-Ax||)");
 semilogy ([0:iter], resvec, "o-g;NO preconditioning: absolute residual;");

 pause (1);
 ## Test Jacobi preconditioner: it will not help much!!!

 M = diag (diag (A)); # Jacobi preconditioner
 [x, flag, relres, iter, resvec] = pcr (A,b,[],maxit,M);
 hold on;
 semilogy ([0:iter],resvec,"o-r;JACOBI preconditioner: absolute residual;");

 pause (1);
 ## Test nonoverlapping block Jacobi preconditioner: this one should give
 ## some convergence speedup!

 M = zeros (N,N); k = 4;
 for i=1:k:N # get k x k diagonal blocks of A
   M(i:i+k-1,i:i+k-1) = A(i:i+k-1,i:i+k-1);
 endfor
 M = [M, zeros(size (M)); zeros(size(M)), -M];
 [x, flag, relres, iter, resvec] = pcr (A,b,[],maxit,M);
 semilogy ([0:iter], resvec, "o-b;BLOCK JACOBI preconditioner: absolute residual;");
 hold off;

Produces the following output

System condition number is 4133.64

and the following figure

Figure 1

Package: octave

	Octave-Forge - Extra packages for GNU Octave
	Home · Packages · Developers · Documentation · FAQ · Bugs · Mailing Lists · Links · Code

Navigation

Demonstration 1

Demonstration 2

Demonstration 3

Demonstration 4