Navigation

Operators and Keywords

Function List:

C++ API

: pp = spline (x, y)
: yi = spline (x, y, xi)

Return the cubic spline interpolant of points x and y.

When called with two arguments, return the piecewise polynomial pp that may be used with ppval to evaluate the polynomial at specific points.

When called with a third input argument, spline evaluates the spline at the points xi. The third calling form spline (x, y, xi) is equivalent to ppval (spline (x, y), xi).

The variable x must be a vector of length n.

y can be either a vector or array. If y is a vector it must have a length of either n or n + 2. If the length of y is n, then the "not-a-knot" end condition is used. If the length of y is n + 2, then the first and last values of the vector y are the values of the first derivative of the cubic spline at the endpoints.

If y is an array, then the size of y must have the form [s1, s2, …, sk, n] or [s1, s2, …, sk, n + 2]. The array is reshaped internally to a matrix where the leading dimension is given by s1 * s2 * … * sk and each row of this matrix is then treated separately. Note that this is exactly the opposite of interp1 but is done for MATLAB compatibility.

See also: pchip, ppval, mkpp, unmkpp.

Demonstration 1

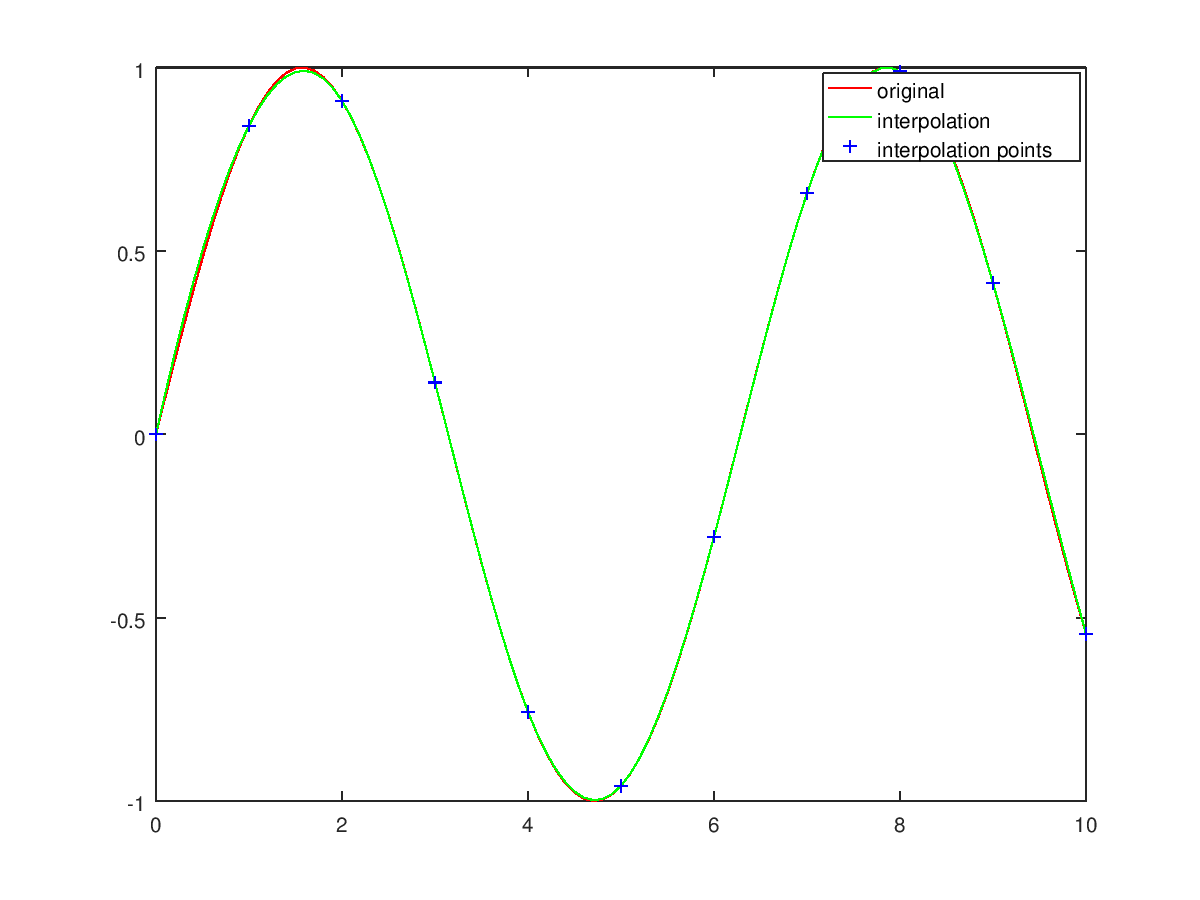
The following code

 x = 0:10; y = sin (x);
 xspline = 0:0.1:10;  yspline = spline (x,y,xspline);
 title ("spline fit to points from sin (x)");
 plot (xspline,sin(xspline),"r", xspline,yspline,"g-", x,y,"b+");
 legend ("original", "interpolation", "interpolation points");
 %--------------------------------------------------------
 % confirm that interpolated function matches the original

Produces the following figure

Figure 1

Package: octave