Navigation

Operators and Keywords

Function List:

C++ API

: trisurf (tri, x, y, z, c)
: trisurf (tri, x, y, z)
: trisurf (…, prop, val, …)
: h = trisurf (…)

Plot a 3-D triangular surface.

In contrast to surf, which plots a surface mesh using rectangles, trisurf plots the mesh using triangles.

tri is typically the output of a Delaunay triangulation over the grid of x, y. Every row of tri represents one triangle and contains three indices into [x, y] which are the vertices of the triangles in the x-y plane. z determines the height above the plane of each vertex.

The color of the trimesh is computed by linearly scaling the z values to fit the range of the current colormap. Use caxis and/or change the colormap to control the appearance.

Optionally, the color of the mesh can be specified independently of z by supplying a color matrix, c. If z has N elements, then c should be an Nx1 vector for colormap data or an Nx3 matrix for RGB data.

Any property/value pairs are passed directly to the underlying patch object.

The optional return value h is a graphics handle to the created patch object.

See also: surf, triplot, trimesh, delaunay, patch, shading.

Demonstration 1

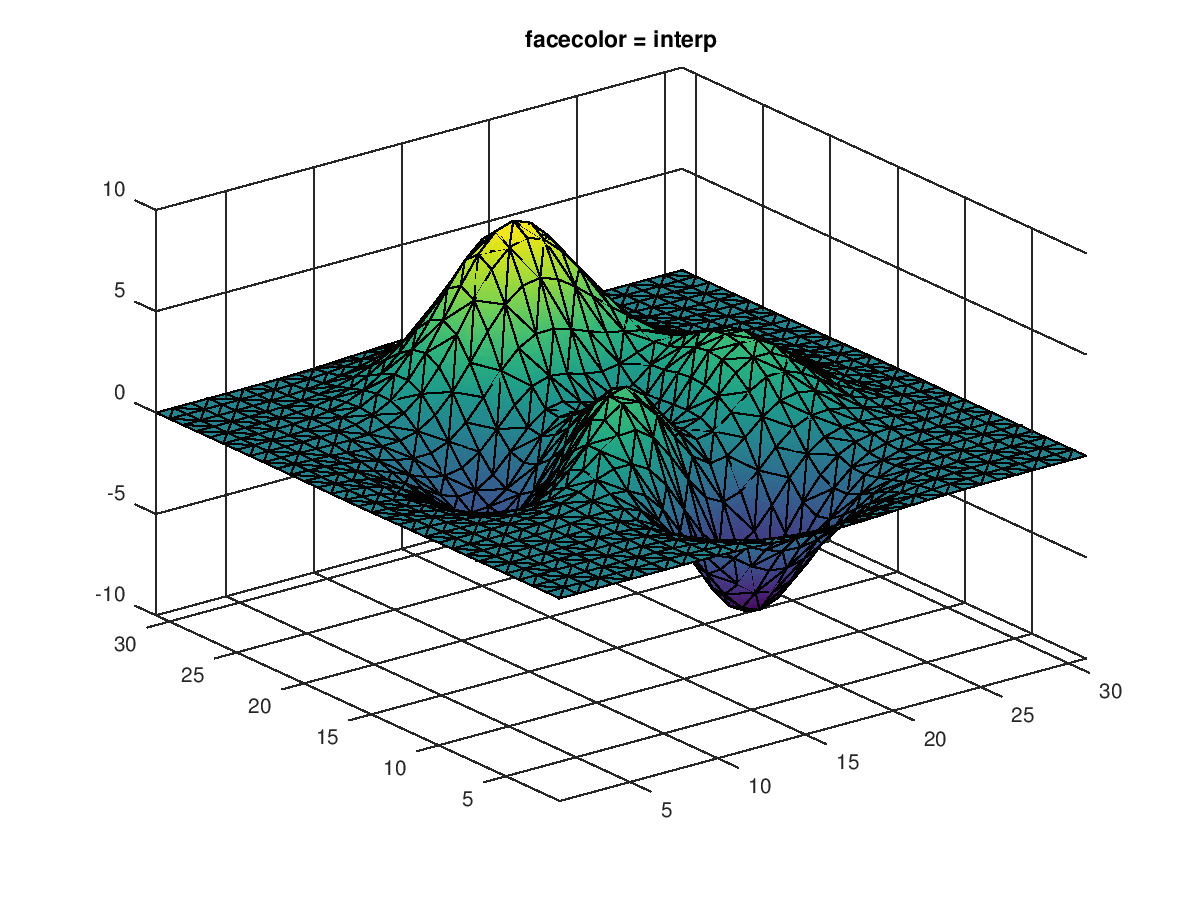
The following code

 clf;
 colormap ("default");
 N = 31;
 [x, y] = meshgrid (1:N);
 tri = delaunay (x(:), y(:));
 z = peaks (N);
 h = trisurf (tri, x, y, z, "facecolor", "interp");
 axis tight;
 zlim auto;
 title (sprintf ("facecolor = %s", get (h, "facecolor")));

Produces the following figure

Figure 1

Demonstration 2

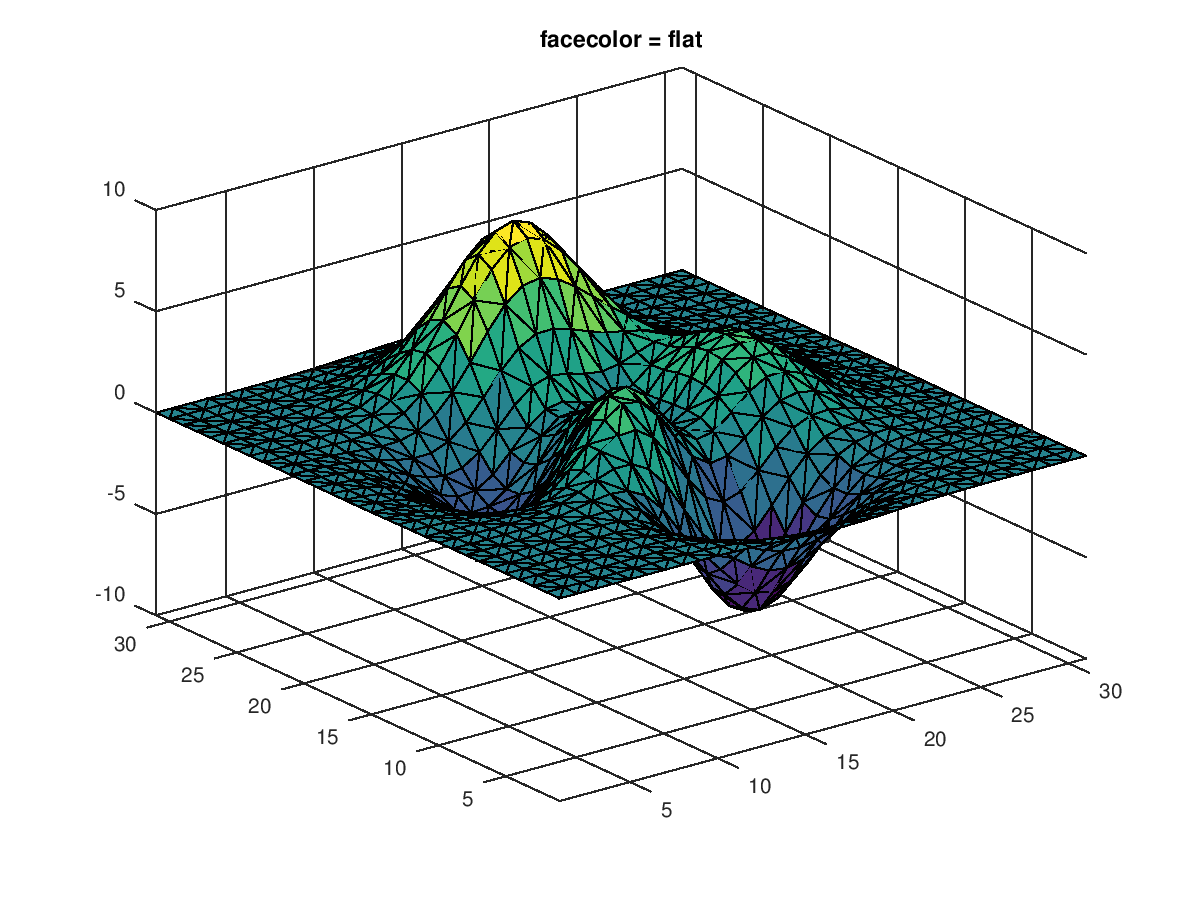
The following code

 clf;
 colormap ("default");
 N = 31;
 [x, y] = meshgrid (1:N);
 tri = delaunay (x(:), y(:));
 z = peaks (N);
 h = trisurf (tri, x, y, z, "facecolor", "flat");
 axis tight;
 zlim auto;
 title (sprintf ("facecolor = %s", get (h, "facecolor")));

Produces the following figure

Figure 1

Demonstration 3

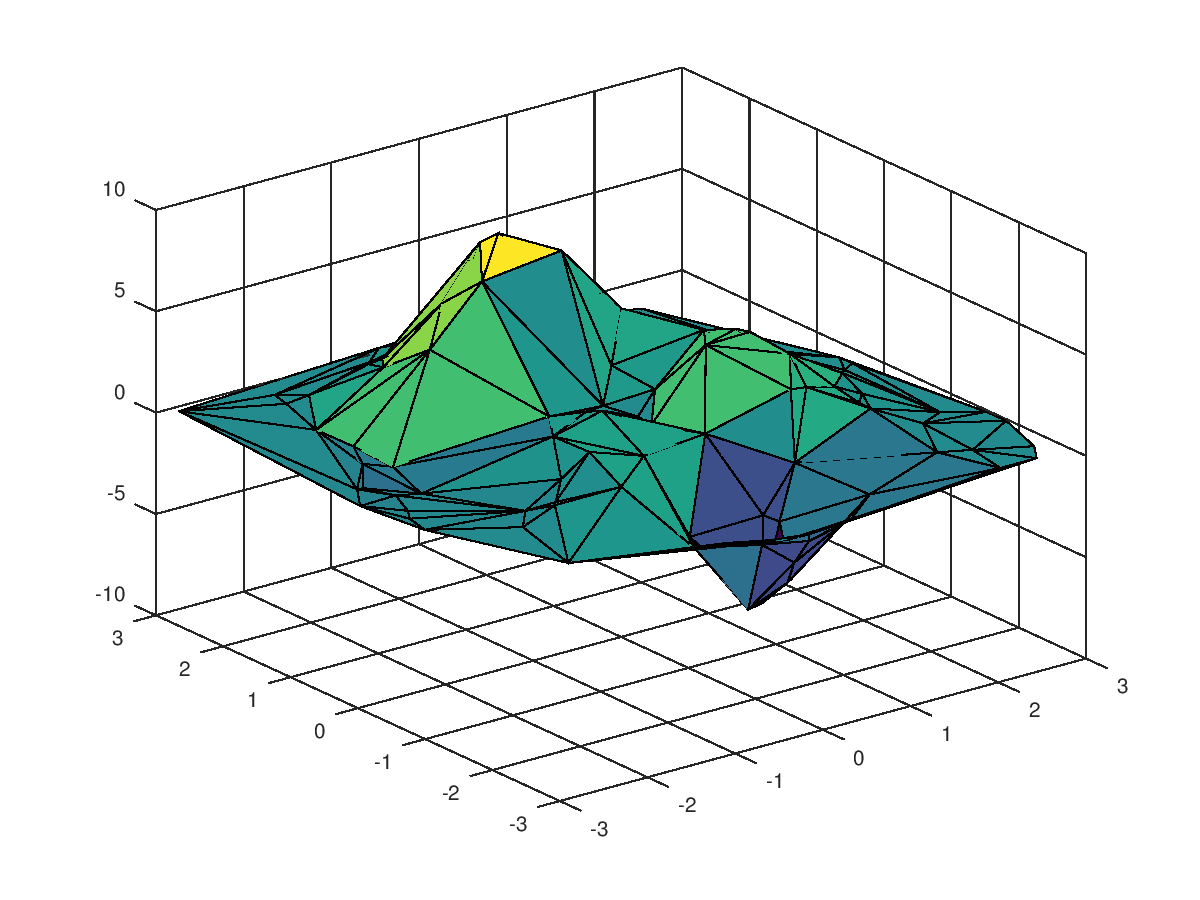
The following code

 clf;
 colormap ("default");
 old_state = rand ("state");
 restore_state = onCleanup (@() rand ("state", old_state));
 rand ("state", 10);
 N = 10;
 x = 3 - 6 * rand (N, N);
 y = 3 - 6 * rand (N, N);
 z = peaks (x, y);
 tri = delaunay (x(:), y(:));
 trisurf (tri, x(:), y(:), z(:));

Produces the following figure

Figure 1

Demonstration 4

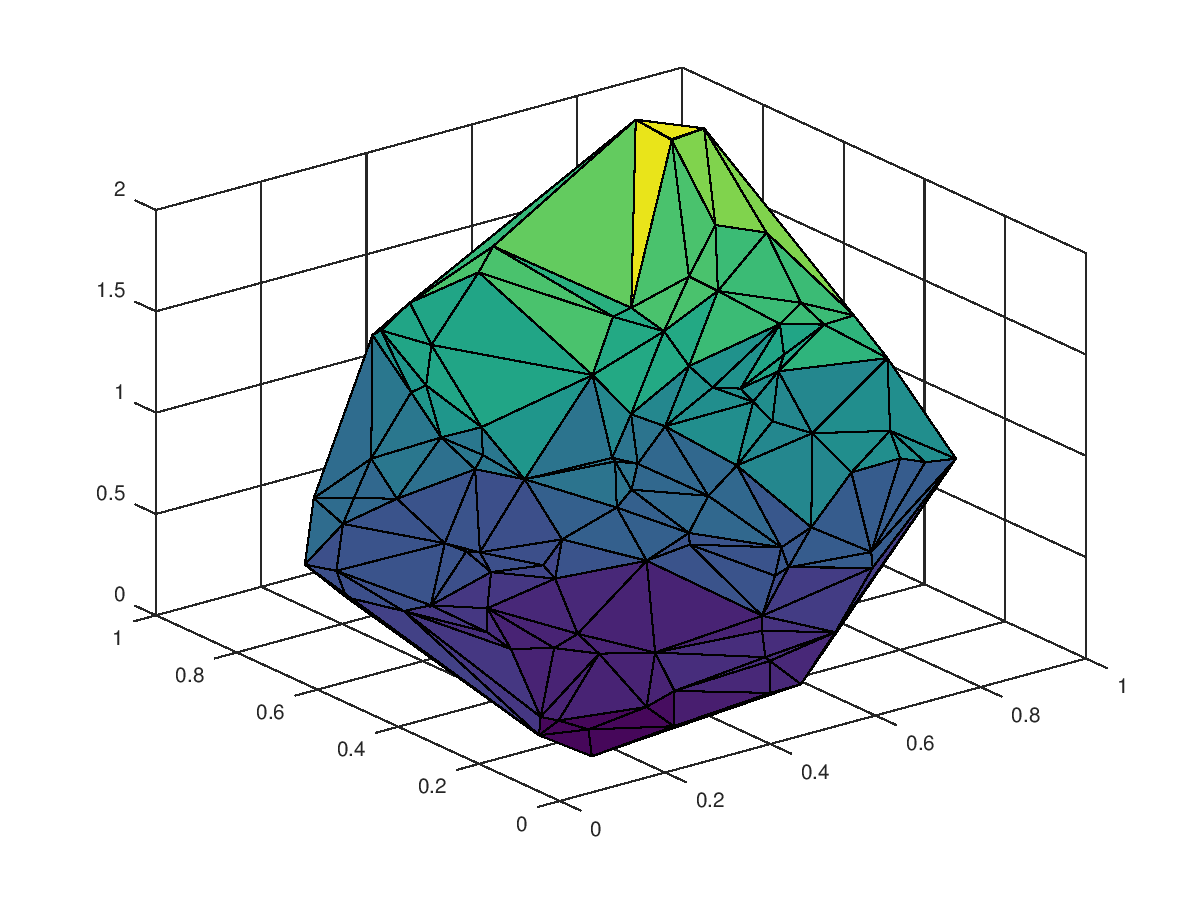
The following code

 clf;
 colormap ("default");
 x = rand (100, 1);
 y = rand (100, 1);
 z = x.^2 + y.^2;
 tri = delaunay (x, y);
 trisurf (tri, x, y, z);

Produces the following figure

Figure 1

Demonstration 5

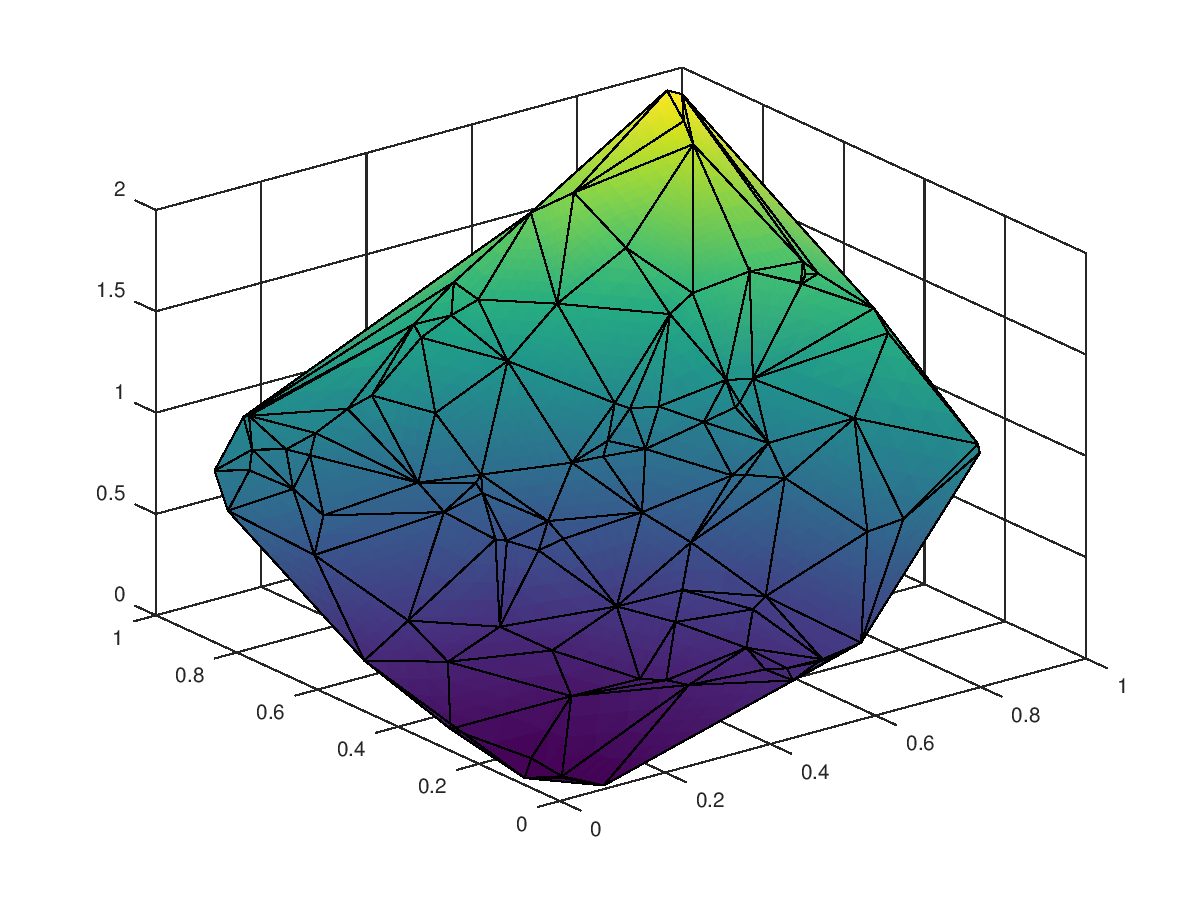
The following code

 clf;
 colormap ("default");
 x = rand (100, 1);
 y = rand (100, 1);
 z = x.^2 + y.^2;
 tri = delaunay (x, y);
 trisurf (tri, x, y, z, "facecolor", "interp");

Produces the following figure

Figure 1

Demonstration 6

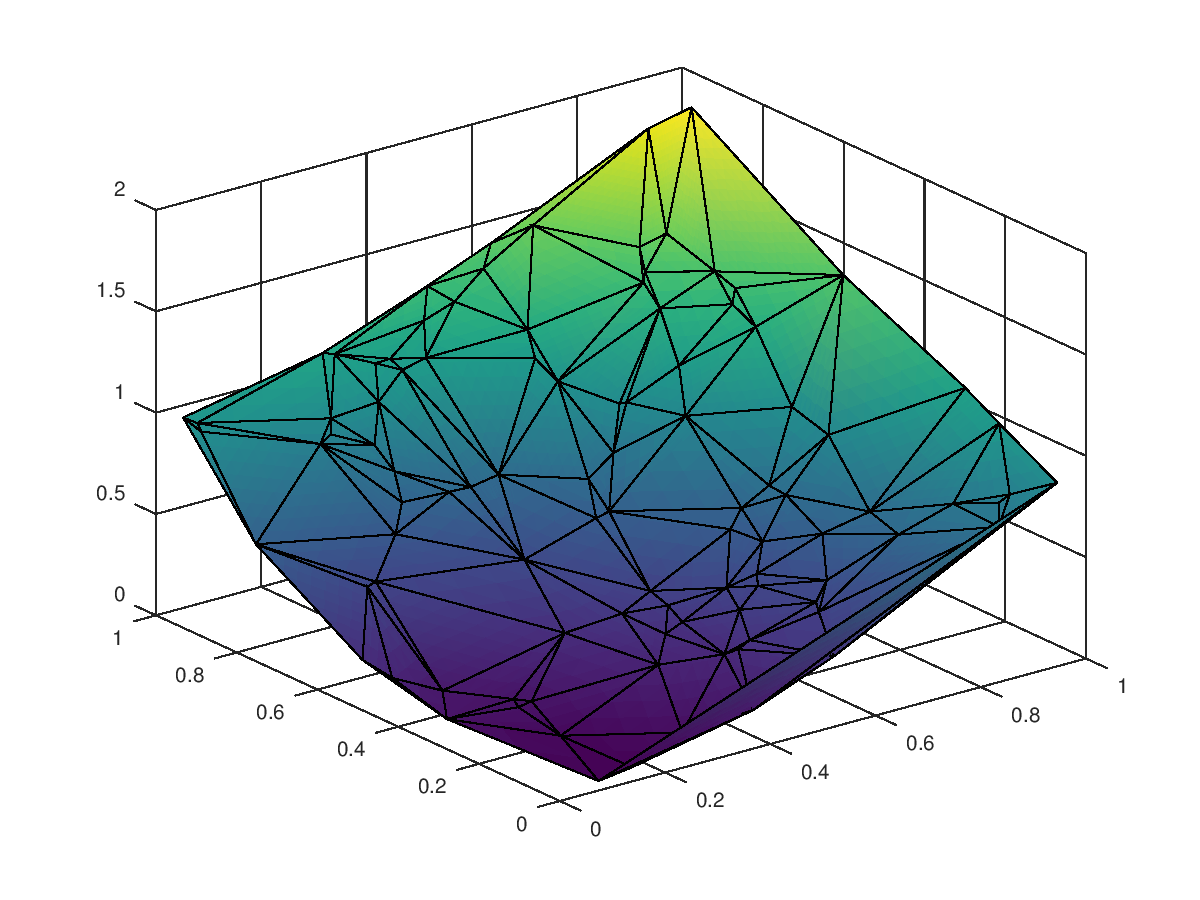
The following code

 clf;
 colormap ("default");
 x = rand (100, 1);
 y = rand (100, 1);
 z = x.^2 + y.^2;
 tri = delaunay (x, y);
 trisurf (tri, x, y, z, "facecolor", "interp", "edgecolor", "k");

Produces the following figure

Figure 1

Package: octave