Function Reference: zernike

Function File: Z = zernike_cartesian (x, y, n)

Function File: Z = zernike_cartesian (x, y, n, limit_r)

Return the cartesian zernikes up to order n (as noll’s index).

If limit_r is false (default true), the polynoms for r>1 are not set to NaN because strictly, the polynoms are only defined for 0 <= r <= 1.

Size of x must be equal size of y.

Demo: type "demo zernike_cartesian"

See also: zernike_name, zernike_noll_to_nm, zernike_polar, zernike_R_poly.

Demonstration 1

The following code

 t = linspace (-1, 1, 80);
 [x, y] = meshgrid (t, t);
 max_order = 16;
 Z = zernike_cartesian (x, y, max_order);
 for k = 1:max_order
   subplot (4, 4, k)
   factors = zeros (max_order, 1);
   factors(k) = 1;
   z = reshape (Z*factors, size (x));
   imagesc (z)
   axis ("off", "equal")
   zname = strrep (zernike_name (k), " ", "\n");
   title (zname)
 endfor

Produces the following figure

Figure 1

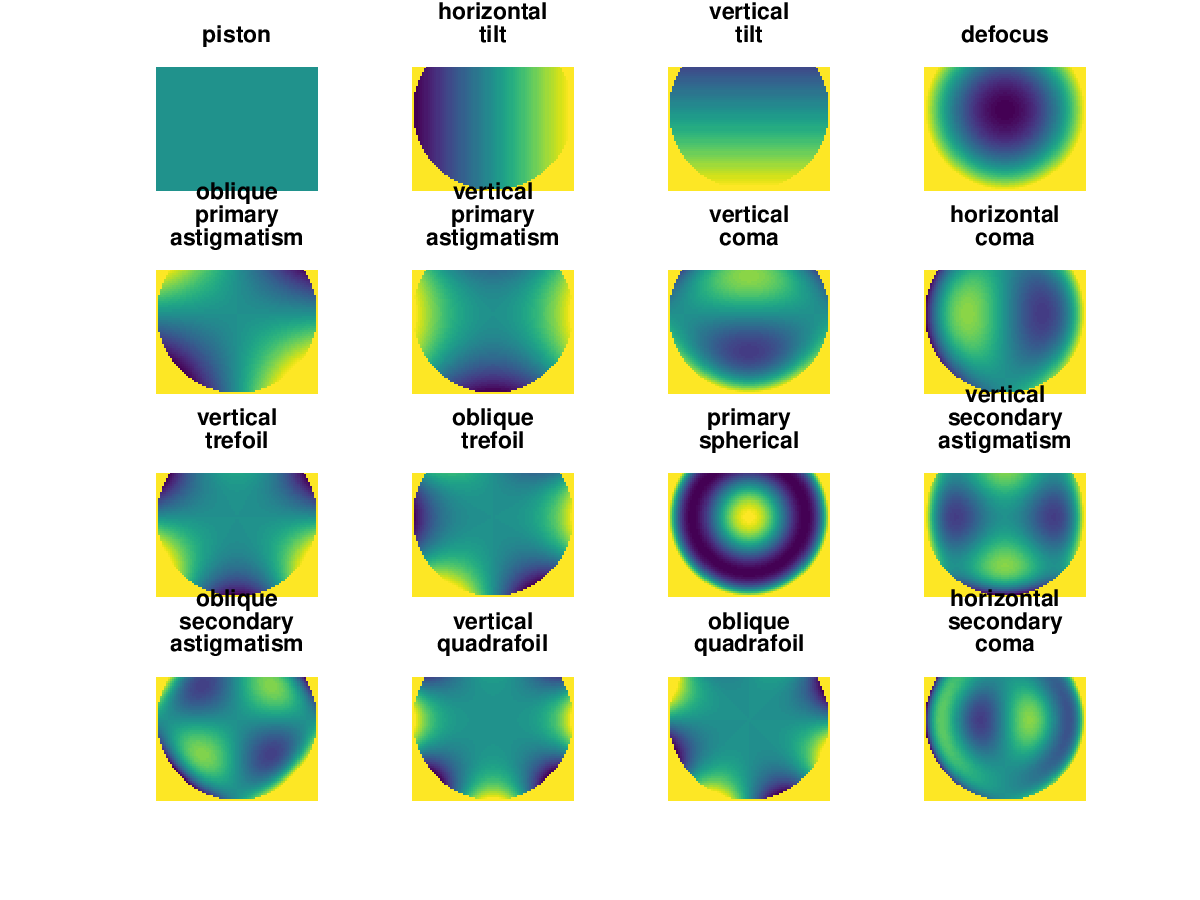Demonstration 2

The following code

 n=30;
 [x,y,z] = sombrero (n);
 z += 0.05 * peaks (x./4, y./4);
 z += 0.02 * x;
 figure
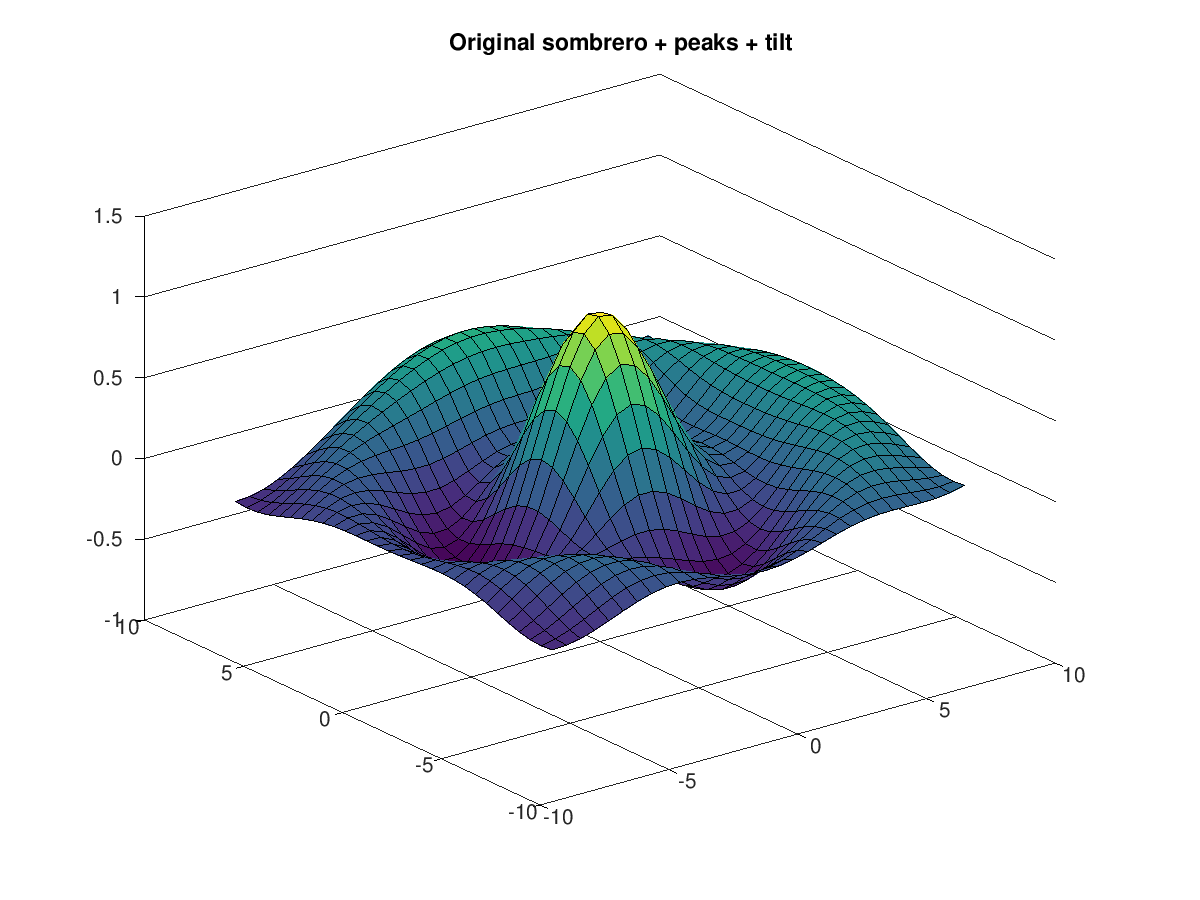
 surf (x, y, z)
 title ("Original sombrero + peaks + tilt");
 
 ## approximate sombrero+peaks
 d = 10;
 x /= d;
 y /= d;
 max_order = 50;
 Z = zernike_cartesian (x, y, max_order, false);
 f = Z\z(:);
 ## create approximated plot
 z_approx = reshape (Z * f, n, n);
 figure
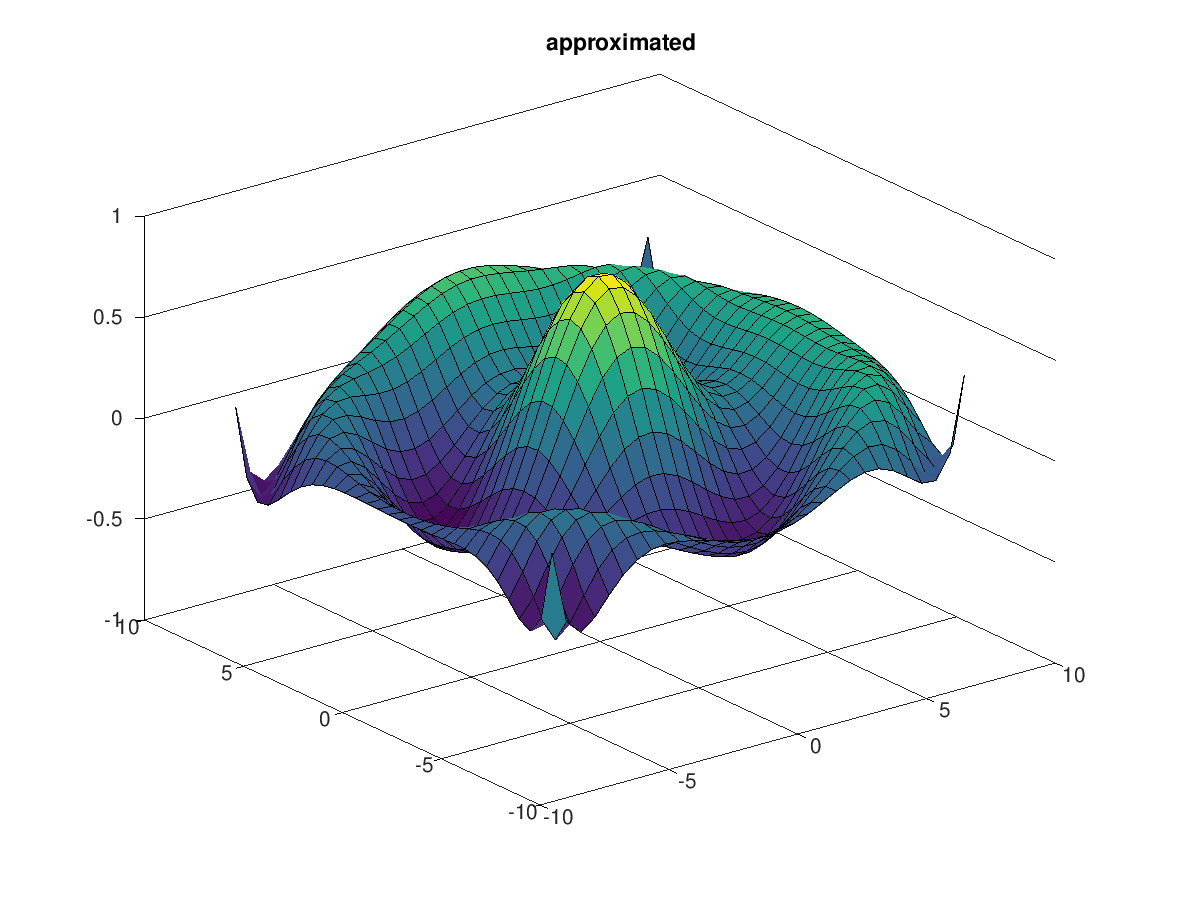
 surf (10 * x, 10 * y, z_approx)
 title ("approximated");

Produces the following figures

Figure 1	Figure 2

Package: optics