- Function File: Df = jacobs (x, f)
- Function File: Df = jacobs (x, f, hook)
Calculate the jacobian of a function using the complex step method.
Let f be a user-supplied function. Given a point x at which we seek for the Jacobian, the function
jacobsreturns the Jacobian matrixd(f(1), …, df(end))/d(x(1), …, x(n)). The function uses the complex step method and thus can be applied to real analytic functions.The optional argument hook is a structure with additional options. hook can have the following fields:
-
h- can be used to define the magnitude of the complex step and defaults to 1e-20; steps larger than 1e-3 are not allowed. -
fixed- is a logical vector internally usable by some optimization functions; it indicates for which elements of x no gradient should be computed, but zero should be returned.
For example:
f = @(x) [x(1)^2 + x(2); x(2)*exp(x(1))]; Df = jacobs ([1, 2], f)
-
Demonstration 1
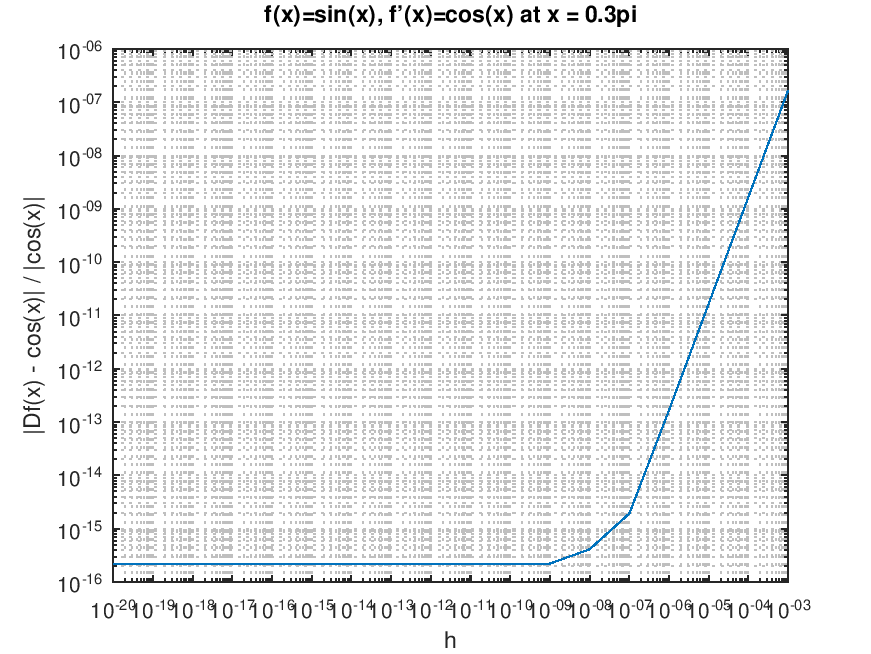
The following code
# Relative error against several h-values
k = 3:20; h = 10 .^ (-k); x = 0.3*pi;
err = zeros (1, numel (k));
for count = 1 : numel (k)
err(count) = abs (jacobs (x, @sin, struct ("h", h(count))) - cos (x)) / abs (cos (x)) + eps;
endfor
loglog (h, err); grid minor;
xlabel ("h"); ylabel ("|Df(x) - cos(x)| / |cos(x)|")
title ("f(x)=sin(x), f'(x)=cos(x) at x = 0.3pi")
Produces the following figure
| Figure 1 |
|---|
 |
Package: optim