- Function File: L = ctmcexps (Q, t, p )
- Function File: L = ctmcexps (Q, p)
-
With three arguments, compute the expected times
L(i)spent in each state i during the time interval [0,t], assuming that the initial occupancy vector is p. With two arguments, compute the expected timeL(i)spent in each transient state i until absorption.Note: In its current implementation, this function requires that an absorbing state is reachable from any non-absorbing state of Q.
INPUTS
Q(i,j)N \times N infinitesimal generator matrix.
Q(i,j)is the transition rate from state i to state j, 1 ≤ i, j ≤ N, i \neq j. The matrix Q must also satisfy the condition \sum_{j=1}^N Q_{i,j} = 0 for every i=1, …, N.tIf given, compute the expected sojourn times in [0,t]
p(i)Initial occupancy probability vector;
p(i)is the probability the system is in state i at time 0, i = 1, …, N
OUTPUTS
L(i)If this function is called with three arguments,
L(i)is the expected time spent in state i during the interval [0,t]. If this function is called with two argumentsL(i)is the expected time spent in transient state i until absorption; if state i is absorbing,L(i)is zero.
See also: dtmcexps.
Demonstration 1
The following code
lambda = 0.5;
N = 4;
b = lambda*[1:N-1];
d = zeros(size(b));
Q = ctmcbd(b,d);
t = linspace(0,10,100);
p0 = zeros(1,N); p0(1)=1;
L = zeros(length(t),N);
for i=1:length(t)
L(i,:) = ctmcexps(Q,t(i),p0);
endfor
plot( t, L(:,1), ";State 1;", "linewidth", 2, ...
t, L(:,2), ";State 2;", "linewidth", 2, ...
t, L(:,3), ";State 3;", "linewidth", 2, ...
t, L(:,4), ";State 4;", "linewidth", 2 );
legend("location","northwest"); legend("boxoff");
xlabel("Time");
ylabel("Expected sojourn time");
Produces the following figure
| Figure 1 |
|---|
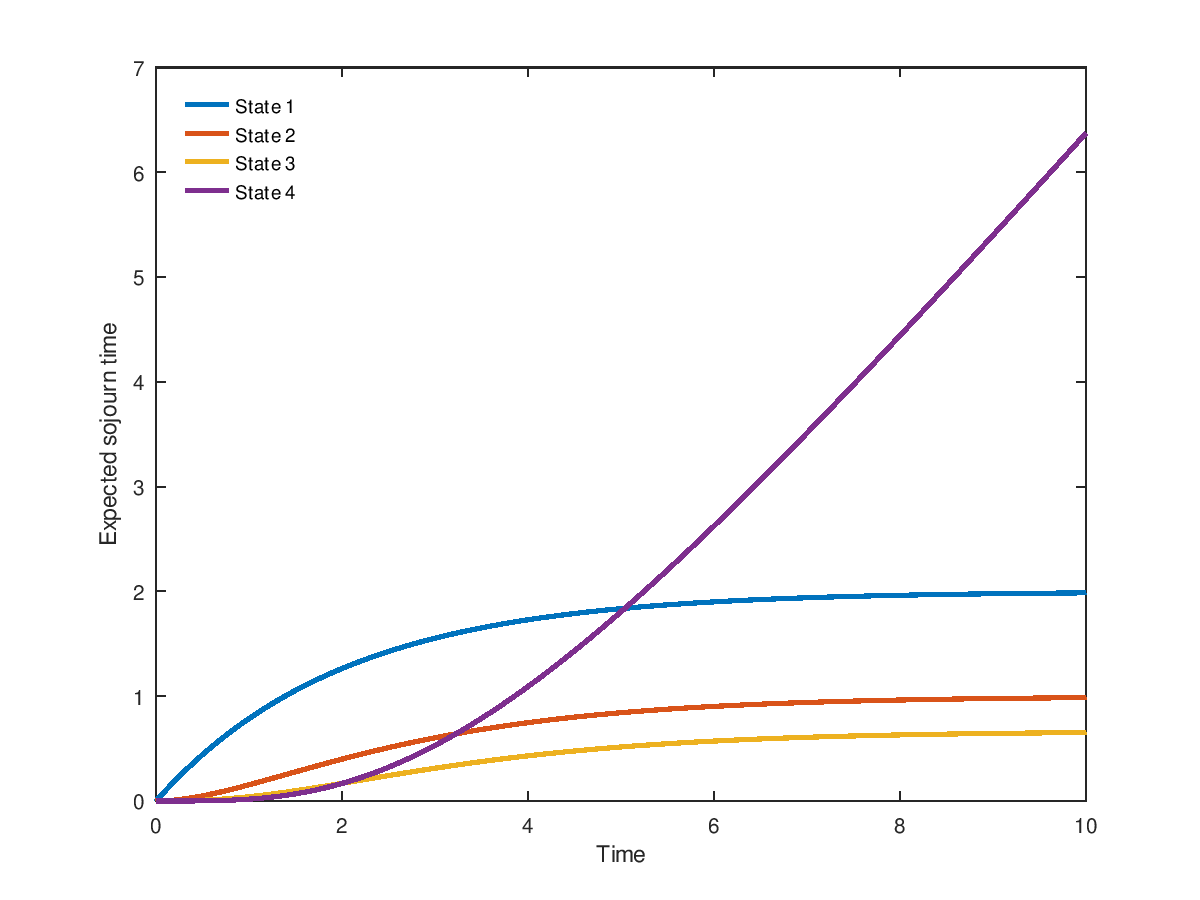 |
Demonstration 2
The following code
lambda = 0.5; N = 4; b = lambda*[1:N-1]; d = zeros(size(b)); Q = ctmcbd(b,d); p0 = zeros(1,N); p0(1)=1; L = ctmcexps(Q,p0); disp(L);
Produces the following output
2.00000 1.00000 0.66667 0.00000
| Figure 1 |
|---|
 |
Package: queueing