Function File: [U, R, Q, X] = qnclosed (N, S, V, …)

This function computes steady-state performance measures of closed queueing networks using the Mean Value Analysis (MVA) algorithm. The qneneing network is allowed to contain fixed-capacity centers, delay centers or general load-dependent centers. Multiple request classes are supported.

This function dispatches the computation to one of qncsemva, qncsmvald or qncmmva.

  • If N is a scalar, the network is assumed to have a single class of requests; in this case, the exact MVA algorithm is used to analyze the network. If S is a vector, then S(k) is the average service time of center k, and this function calls qncsmva which supports load-independent service centers. If S is a matrix, S(k,i) is the average service time at center k when i=1, …, N jobs are present; in this case, the network is analyzed with the qncmmvald function.
  • If N is a vector, the network is assumed to have multiple classes of requests, and is analyzed using the exact multiclass MVA algorithm as implemented in the qncmmva function.

See also: qncsmva, qncsmvald, qncmmva.

Demonstration 1

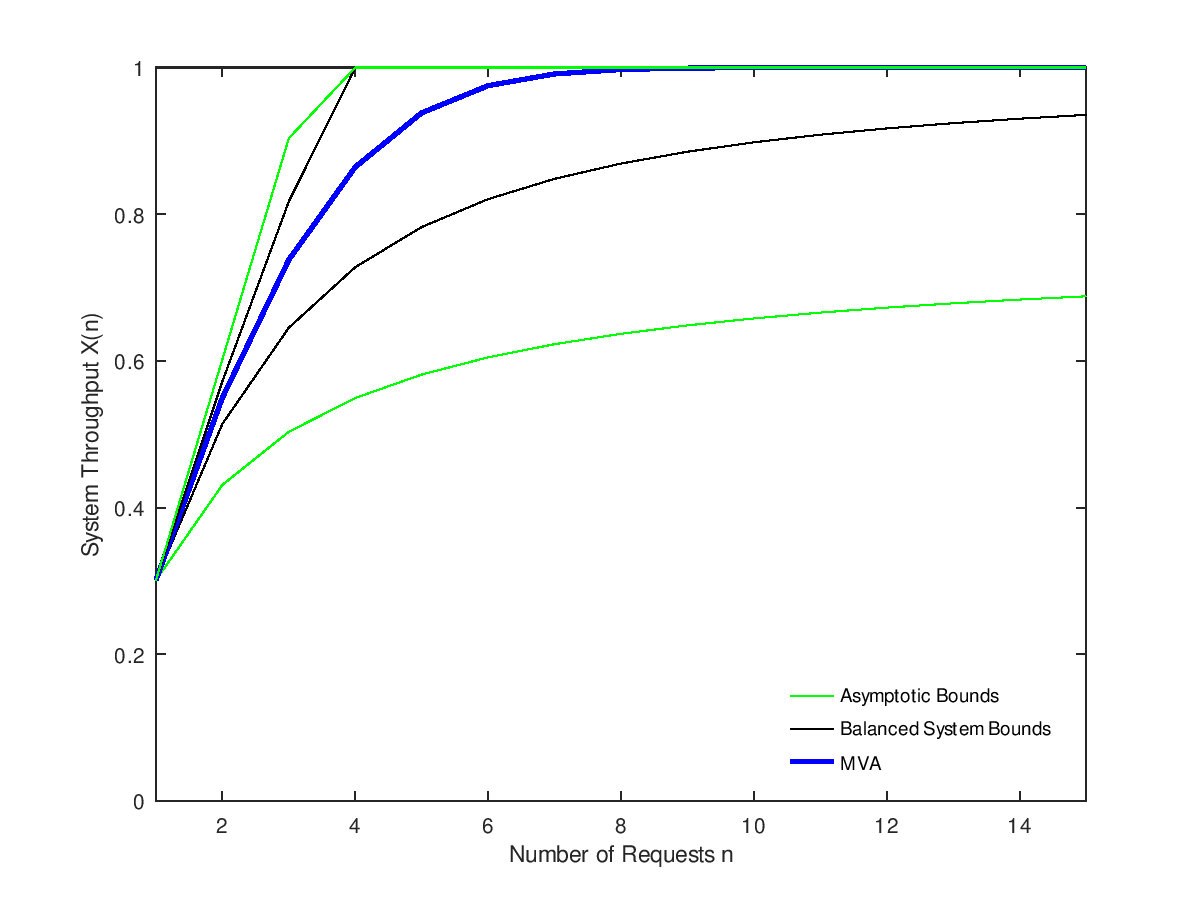
The following code

 P = [0 0.3 0.7; 1 0 0; 1 0 0]; # Transition probability matrix
 S = [1 0.6 0.2];               # Average service times
 m = ones(size(S));             # All centers are single-server
 Z = 2;                         # External delay
 N = 15;                        # Maximum population to consider
 V = qncsvisits(P);             # Compute number of visits
 X_bsb_lower = X_bsb_upper = X_ab_lower = X_ab_upper = X_mva = zeros(1,N);
 for n=1:N
   [X_bsb_lower(n) X_bsb_upper(n)] = qncsbsb(n, S, V, m, Z);
   [X_ab_lower(n) X_ab_upper(n)] = qncsaba(n, S, V, m, Z);
   [U R Q X] = qnclosed( n, S, V, m, Z );
   X_mva(n) = X(1)/V(1);
 endfor
 close all;
 plot(1:N, X_ab_lower,"g;Asymptotic Bounds;", ...
      1:N, X_bsb_lower,"k;Balanced System Bounds;", ...
      1:N, X_mva,"b;MVA;", "linewidth", 2, ...
      1:N, X_bsb_upper,"k", 1:N, X_ab_upper,"g" );
 axis([1,N,0,1]); legend("location","southeast"); legend("boxoff");
 xlabel("Number of Requests n"); ylabel("System Throughput X(n)");

Produces the following figure

Figure 1

Package: queueing