Function Reference: qncmmva

Function File: [U, R, Q, X] = qncmmva (N, S )

Function File: [U, R, Q, X] = qncmmva (N, S, V)

Function File: [U, R, Q, X] = qncmmva (N, S, V, m)

Function File: [U, R, Q, X] = qncmmva (N, S, V, m, Z)

Function File: [U, R, Q, X] = qncmmva (N, S, P)

Function File: [U, R, Q, X] = qncmmva (N, S, P, r)

Function File: [U, R, Q, X] = qncmmva (N, S, P, r, m)

Compute steady-state performance measures for closed, multiclass queueing networks using the Mean Value Analysys (MVA) algorithm.

Queueing policies at service centers can be any of the following:

FCFS: (First-Come-First-Served) customers are served in order of arrival; multiple servers are allowed. For this kind of queueing discipline, average service times must be class-independent.
PS: (Processor Sharing) customers are served in parallel by a single server, each customer receiving an equal share of the service rate.
LCFS-PR: (Last-Come-First-Served, Preemptive Resume) customers are served in reverse order of arrival by a single server and the last arrival preempts the customer in service who will later resume service at the point of interruption.
IS: (Infinite Server) customers are delayed independently of other customers at the service center (there is effectively an infinite number of servers).

INPUTS

N(c): number of class c requests; N(c) ≥ 0. If class c has no requests (N(c) == 0), then for all k, this function returns U(c,k) = R(c,k) = Q(c,k) = X(c,k) = 0
S(c,k): mean service time for class c requests at center k (S(c,k) ≥ 0). If the service time at center k is class-dependent, then center k is assumed to be of type -/G/1–PS (Processor Sharing). If center k is a FCFS node (m(k)>1), then the service times must be class-independent, i.e., all classes must have the same service time.
V(c,k): average number of visits of class c requests at center k; V(c,k) ≥ 0, default is 1. If you pass this argument, class switching is not allowed
P(r,i,s,j): probability that a class r request completing service at center i is routed to center j as a class s request; the reference stations for each class are specified with the paramter r. If you pass argument P, class switching is allowed; however, you can not specify any external delay (i.e., Z must be zero) and all servers must be fixed-rate or infinite-server nodes (m(k) ≤ 1 for all k).
r(c): reference station for class c. If omitted, station 1 is the reference station for all classes. See qncmvisits.
m(k): If m(k)<1, then center k is assumed to be a delay center (IS node -/G/\infty). If m(k)==1, then service center k is a regular queueing center (M/M/1–FCFS, -/G/1–LCFS-PR or -/G/1–PS). Finally, if m(k)>1, center k is a M/M/m–FCFS center with m(k) identical servers. Default is m(k)=1 for each k.
Z(c): class c external delay (think time); Z(c) ≥ 0. Default is 0. This parameter can not be used if you pass a routing matrix as the second parameter of qncmmva.

OUTPUTS

U(c,k): If k is a FCFS, LCFS-PR or PS node (m(k) ≥ 1), then U(c,k) is the class c utilization at center k, 0 ≤ U(c,k) ≤ 1. If k is an IS node, then U(c,k) is the class c traffic intensity at center k, defined as U(c,k) = X(c,k)*S(c,k). In this case the value of U(c,k) may be greater than one.
R(c,k): class c response time at center k. The class c residence time at center k is R(c,k) * C(c,k). The total class c system response time is dot(R, V, 2).
Q(c,k): average number of class c requests at center k. The total number of requests at center k is sum(Q(:,k)). The total number of class c requests in the system is sum(Q(c,:)).
X(c,k): class c throughput at center k. The class c throughput can be computed as X(c,1) / V(c,1).

NOTES

If the function call specifies the visit ratios V, then class switching is not allowed. If the function call specifies the routing probability matrix P, then class switching is allowed; however, in this case all nodes are restricted to be fixed rate servers or delay centers: multiple-server and general load-dependent centers are not supported.

In presence of load-dependent servers (e.g., if m(i)>1 for some i), the MVA algorithm is known to be numerically unstable. Generally this problem shows up as negative values for the computed response times or utilizations. This is not a problem with the queueing package, but with the MVA algorithm; as such, there is no known workaround at the moment (aoart from using a different solution technique, if available). This function prints a warning if it detects numerical problems; you can disable the warning with the command warning("off", "qn:numerical-instability").

Given a network with K service centers, C job classes and population vector {\bf N}=\left[N_1, …, N_C\right], the MVA algorithm requires space O(C \prod_i (N_i + 1)). The time complexity is O(CK\prod_i (N_i + 1)). This implementation is slightly more space-efficient (see details in the code). While the space requirement can be mitigated by using some optimizations, the time complexity can not. If you need to analyze large closed networks you should consider the qncmmvaap function, which implements the approximate MVA algorithm. Note however that qncmmvaap will only provide approximate results.

REFERENCES

M. Reiser and S. S. Lavenberg, Mean-Value Analysis of Closed Multichain Queuing Networks, Journal of the ACM, vol. 27, n. 2, April 1980, pp. 313–322. 10.1145/322186.322195

This implementation is based on G. Bolch, S. Greiner, H. de Meer and K. Trivedi, Queueing Networks and Markov Chains: Modeling and Performance Evaluation with Computer Science Applications, Wiley, 1998 and Edward D. Lazowska, John Zahorjan, G. Scott Graham, and Kenneth C. Sevcik, Quantitative System Performance: Computer System Analysis Using Queueing Network Models, Prentice Hall, 1984. http://www.cs.washington.edu/homes/lazowska/qsp/. In particular, see section 7.4.2.1 ("Exact Solution Techniques").

See also: qnclosed, qncmmvaapprox, qncmvisits.

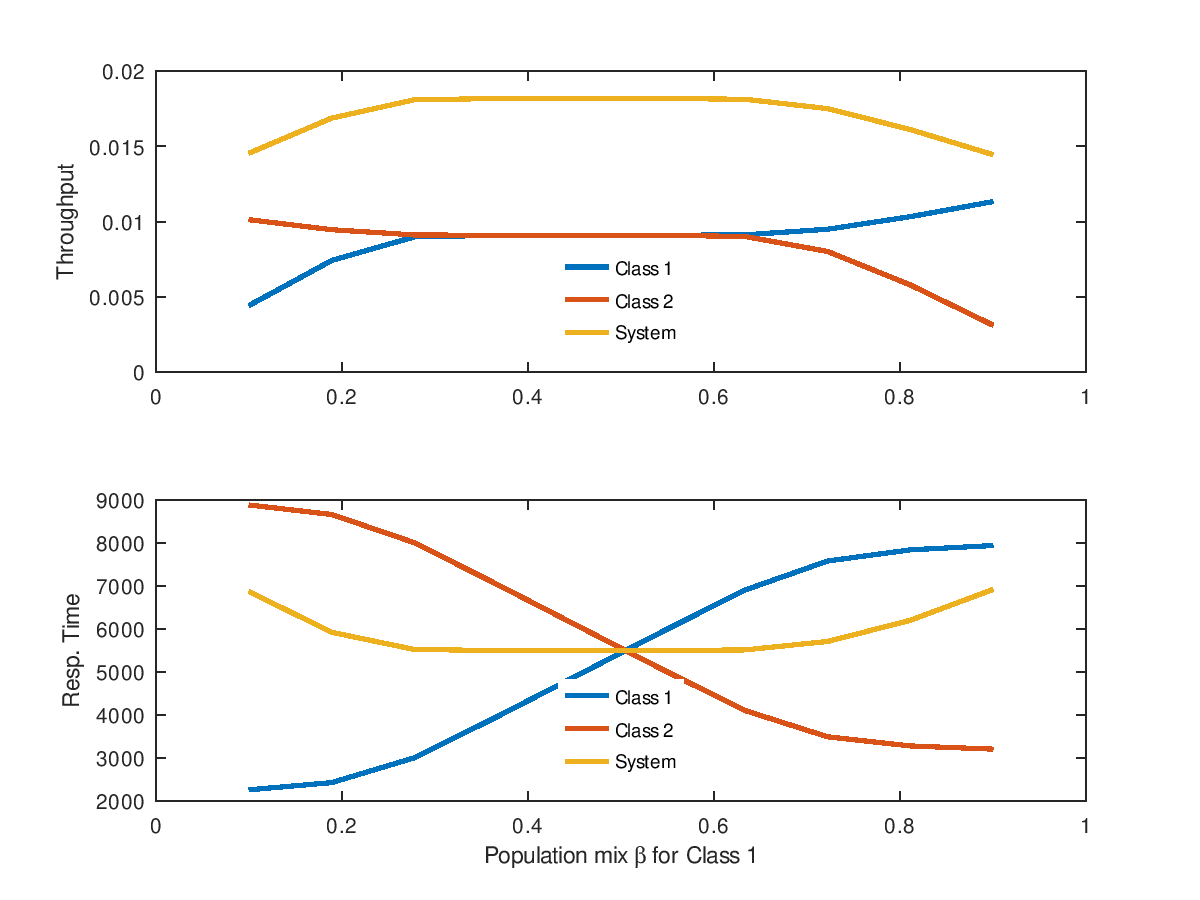
Demonstration 1

The following code

 Ntot = 100; # total population size
 b = linspace(0.1,0.9,10); # fractions of class-1 requests
 S = [20 80 31 14 23 12; ...
      90 30 33 20 14 7];
 V = ones(size(S));
 X1 = X1 = XX = zeros(size(b));
 R1 = R2 = RR = zeros(size(b));
 for i=1:length(b)
   N = [fix(b(i)*Ntot) Ntot-fix(b(i)*Ntot)];
   # printf("[%3d %3d]\n", N(1), N(2) );
   [U R Q X] = qncmmva( N, S, V );
   X1(i) = X(1,1) / V(1,1);
   X2(i) = X(2,1) / V(2,1);
   XX(i) = X1(i) + X2(i);
   R1(i) = dot(R(1,:), V(1,:));
   R2(i) = dot(R(2,:), V(2,:));
   RR(i) = Ntot / XX(i);
 endfor
 subplot(2,1,1);
 plot(b, X1, ";Class 1;", "linewidth", 2, ...
      b, X2, ";Class 2;", "linewidth", 2, ...
      b, XX, ";System;", "linewidth", 2 );
 legend("location","south"); legend("boxoff");
 ylabel("Throughput");
 subplot(2,1,2);
 plot(b, R1, ";Class 1;", "linewidth", 2, ...
      b, R2, ";Class 2;", "linewidth", 2, ...
      b, RR, ";System;", "linewidth", 2 );
 legend("location","south"); legend("boxoff");
 xlabel("Population mix \\beta for Class 1");
 ylabel("Resp. Time");

Produces the following figure

Figure 1

Demonstration 2

The following code

 S = [1 0 .025; 0 15 .5];
 P = zeros(2,3,2,3);
 P(1,1,1,3) = P(1,3,1,1) = 1;
 P(2,2,2,3) = P(2,3,2,2) = 1;
 V = qncmvisits(P,[3 3]); # reference station is station 3
 N = [15 5];
 m = [-1 -1 1];
 [U R Q X] = qncmmva(N,S,V,m)

Produces the following output

U =

   14.32312   -0.00000    0.35808
   -0.00000    4.70699    0.15690

R =

    1.00000    0.00000    0.04726
    0.00000   15.00000    0.93374

Q =

   14.32312   -0.00000    0.67688
   -0.00000    4.70699    0.29301

X =

   14.32312   -0.00000   14.32312
   -0.00000    0.31380    0.31380

Figure 1

Demonstration 3

The following code

 C = 2; K = 3;
 S = [.01 .07 .10; ...
      .05 .07 .10 ];
 P = zeros(C,K,C,K);
 P(1,1,1,2) = .7; P(1,1,1,3) = .2; P(1,1,2,1) = .1;
 P(2,1,2,2) = .3; P(2,1,2,3) = .5; P(2,1,1,1) = .2;
 P(1,2,1,1) = P(2,2,2,1) = 1;
 P(1,3,1,1) = P(2,3,2,1) = 1;
 N = [3 0];
 [U R Q X] = qncmmva(N, S, P)

Produces the following output

U =

   0.12609   0.61784   0.25218
   0.31522   0.13239   0.31522

R =

   0.014653   0.133148   0.163256
   0.073266   0.133148   0.163256

Q =

   0.18476   1.17519   0.41170
   0.46190   0.25183   0.51462

X =

   12.6089    8.8262    2.5218
    6.3044    1.8913    3.1522

Figure 1

Package: queueing