- Function File: [U, R, Q, X, p0, pK] = qsmm1k (lambda, mu, K)
- Function File: pn = qsmm1k (lambda, mu, K, n)
-
Compute utilization, response time, average number of requests and throughput for a M/M/1/K finite capacity system.
In a M/M/1/K queue there is a single server and a queue with finite capacity: the maximum number of requests in the system (including the request being served) is K, and the maximum queue length is therefore K-1.
INPUTS
lambdaArrival rate (
lambda>0).muService rate (
mu>0).KMaximum number of requests allowed in the system (
K ≥ 1).nNumber of requests in the (
0 ≤ n ≤ K).
OUTPUTS
UService center utilization, which is defined as
U = 1-p0RService center response time
QAverage number of requests in the system
XService center throughput
p0Steady-state probability that there are no requests in the system
pKSteady-state probability that there are K requests in the system (i.e., that the system is full)
pnSteady-state probability that there are n requests in the system (including the one being served).
If this function is called with less than four arguments, lambda, mu and K can be vectors of the same size. In this case, the results will be vectors as well.
See also: qsmm1,qsmminf,qsmmm.
Demonstration 1
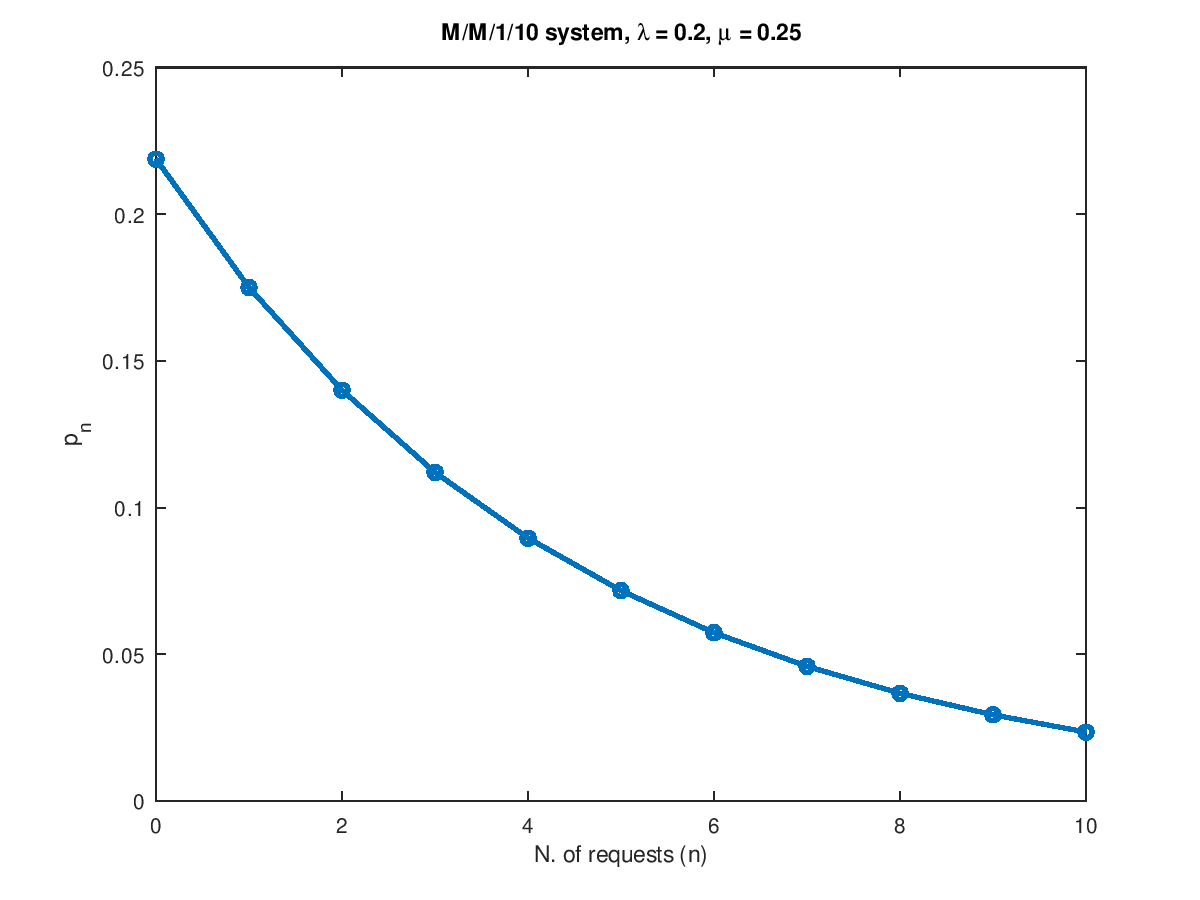
The following code
## Given a M/M/1/K queue, compute the steady-state probability pk
## of having n requests in the systen.
lambda = 0.2;
mu = 0.25;
K = 10;
n = 0:10;
pn = qsmm1k(lambda, mu, K, n);
plot(n, pn, "-o", "linewidth", 2);
xlabel("N. of requests (n)");
ylabel("p_n");
title(sprintf("M/M/1/%d system, \\lambda = %g, \\mu = %g", K, lambda, mu));
Produces the following figure
| Figure 1 |
|---|
 |
Package: queueing