- Function File:
[rmsx,w] =movingrms(x,w,rc,Fs=1)¶ Calculate moving RMS value of the signal in x.
The signal is convoluted against a sigmoid window of width w and risetime rc. The units of these parameters are relative to the value of the sampling frequency given in Fs (Default value = 1).
Run
demo movingrmsto see an example.See also: sigmoid_train.
Demonstration 1
The following code
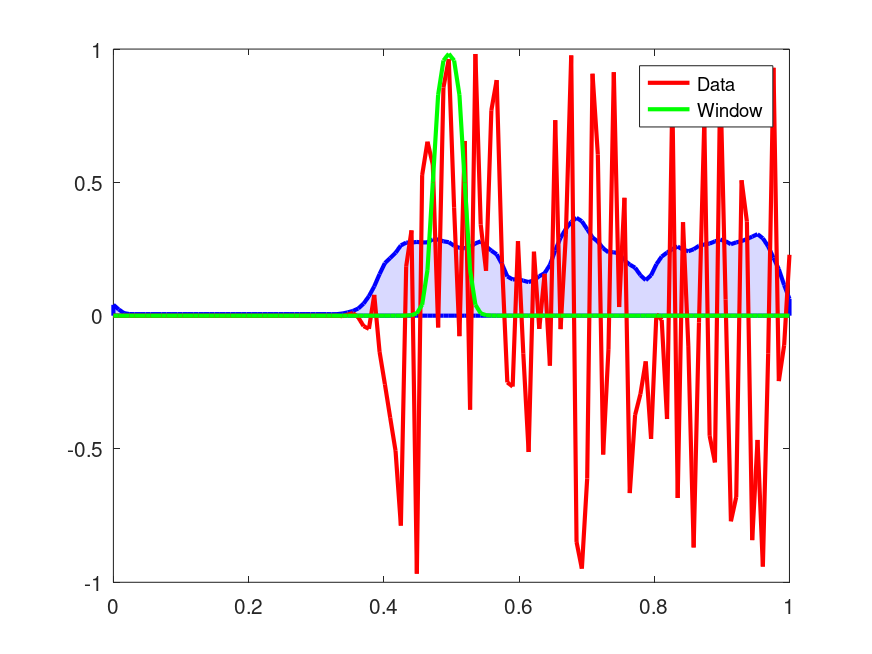
N = 128; t = linspace(0,1,N)'; x = sigmoid_train (t,[0.4 inf],1e-2).*(2*rand(size(t))-1); Fs = 1/diff(t(1:2)); width = 0.05; rc = 5e-3; [wx w] = movingrms (zscore (x),width,rc,Fs); area (t,wx,'facecolor',[0.85 0.85 1],'edgecolor','b','linewidth',2); hold on; h = plot (t,x,'r-;Data;',t,w,'g-;Window;'); set (h, 'linewidth', 2); hold off; # --------------------------------------------------------------------------- # The shaded plot shows the local RMS of the Data: white noise with onset at # aprox. t== 0.4. # The observation window is also shown.
Produces the following figure
| Figure 1 |
|---|
 |
Demonstration 2
The following code
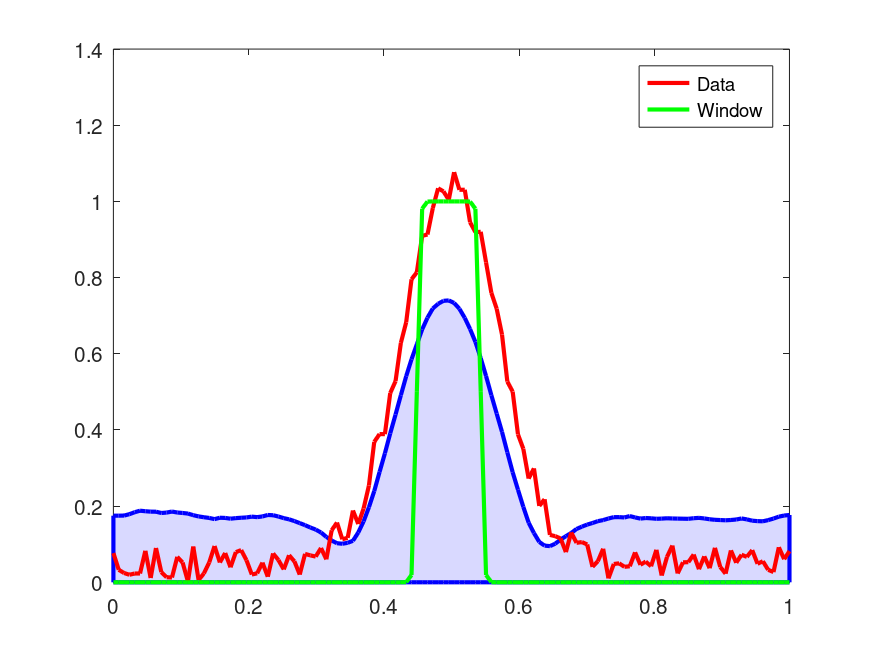
N = 128; t = linspace(0,1,N)'; x = exp(-((t-0.5)/0.1).^2) + 0.1*rand(N,1); Fs = 1/diff(t(1:2)); width = 0.1; rc = 2e-3; [wx w] = movingrms (zscore (x),width,rc,Fs); area (t,wx,'facecolor',[0.85 0.85 1],'edgecolor','b','linewidth',2); hold on; h = plot (t,x,'r-;Data;',t,w,'g-;Window;'); set (h, 'linewidth', 2); hold off; # --------------------------------------------------------------------------- # The shaded plot shows the local RMS of the Data: Gausian with centered at # aprox. t== 0.5. # The observation window is also shown.
Produces the following figure
| Figure 1 |
|---|
 |
Package: signal