- Function File:
F =primitive(f, t, F0)¶ Calculate the primitive of a function.
The function approximates the primitive (indefinite integral) of the univariate function handle f with constant of integration F0. The output is the primitive evaluated at the points t. The vector t must be ordered and ascending.
This function is a fancy way of calculating the cumulative sum,
F = cumsum (f(t).*diff (t)([1 1:end])).Example:
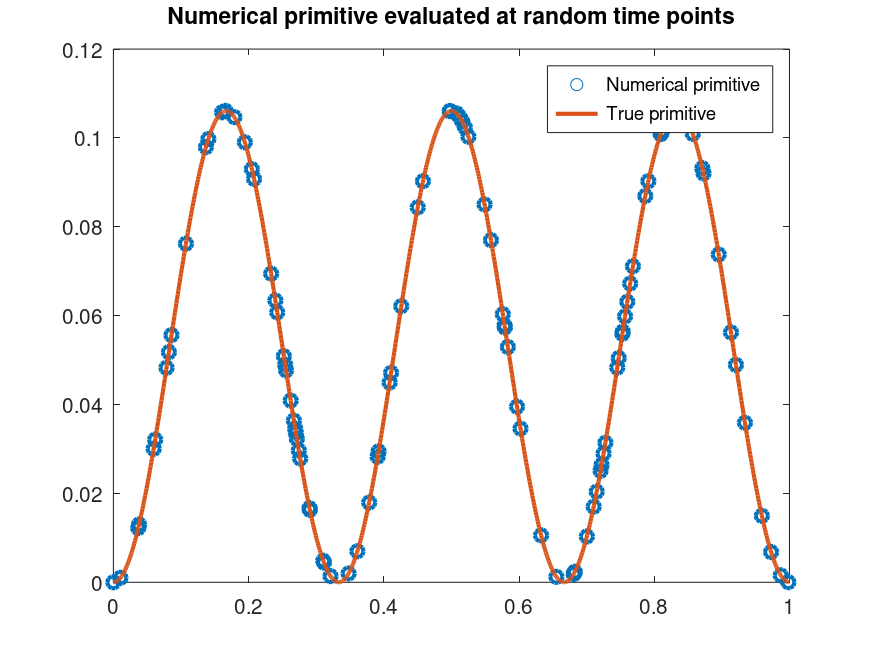
f = @(t) sin (2 * pi * 3 * t); t = [0; sort(rand (100, 1))]; F = primitive (f, t, 0); t_true = linspace (0, 1, 1e3).'; F_true = (1 - cos (2 * pi * 3 * t_true)) / (2 * pi * 3); plot (t, F, 'o', t_true, F_true);
See also: quadgk, cumsum.
Demonstration 1
The following code
f = @(t) sin (2*pi*3*t);
t = [0; sort(rand (100, 1))];
F = primitive (f, t, 0);
t_true = linspace (0, 1, 1e3).';
F_true = (1 - cos (2 * pi * 3 * t_true)) / (2 * pi * 3);
h = plot (t, F, "o;Numerical primitive;", t_true, F_true, "-;True primitive;");
set (h, "linewidth", 2);
title ("Numerical primitive evaluated at random time points");
Produces the following figure
| Figure 1 |
|---|
 |
Package: signal