Function Reference: sgolayfilt

Function File: y = sgolayfilt (x) ¶

Function File: y = sgolayfilt (x, p) ¶

Function File: y = sgolayfilt (x, p, n) ¶

Function File: y = sgolayfilt (x, p, n, m) ¶

Function File: y = sgolayfilt (x, p, n, m, ts) ¶

Function File: y = sgolayfilt (x, f) ¶

Smooth the data in x with a Savitsky-Golay smoothing filter of polynomial order p and length n, n odd, n > p. By default, p=3 and n=p+2 or n=p+3 if p is even.

If f is given as a matrix, it is expected to be a filter as computed by sgolay.

These filters are particularly good at preserving lineshape while removing high frequency squiggles. Particularly, compare a 5 sample averager, an order 5 butterworth lowpass filter (cutoff 1/3) and sgolayfilt(x, 3, 5), the best cubic estimated from 5 points:

[b, a] = butter (5, 1/3);
x = [zeros(1,15), 10*ones(1,10), zeros(1,15)];
plot (sgolayfilt (x), "r;sgolayfilt;", ...
      filtfilt (ones (1,5)/5, 1, x), "g;5 sample average;", ...
      filtfilt (b, a, x), "c;order 5 butterworth;", ...
      x, "+b;original data;");

See also: sgolay.

Demonstration 1

The following code

 [b, a] = butter(5,1/3);
 x=[zeros(1,15), 10*ones(1,10), zeros(1,15)];
 subplot(121);
 plot(sgolayfilt(x),"r;sgolay(3,5);",...
      filtfilt(ones(1,5)/5,1,x),"g;5 sample average;",...
      filtfilt(b,a,x),"c;order 5 butterworth;",...
      x,"+b;original data;");
 axis([1 40 -2 15]);
 title("boxcar");

 x=x+randn(size(x))/2;
 subplot(122);
 plot(sgolayfilt(x,3,5),"r;sgolay(3,5);",...
      filtfilt(ones(1,5)/5,1,x),"g;5 sample average;",...
      filtfilt(b,a,x),"c;order 5 butterworth;",...
      x,"+b;original data;");
 axis([1 40 -2 15]);
 title("boxcar+noise");

Produces the following figure

Figure 1

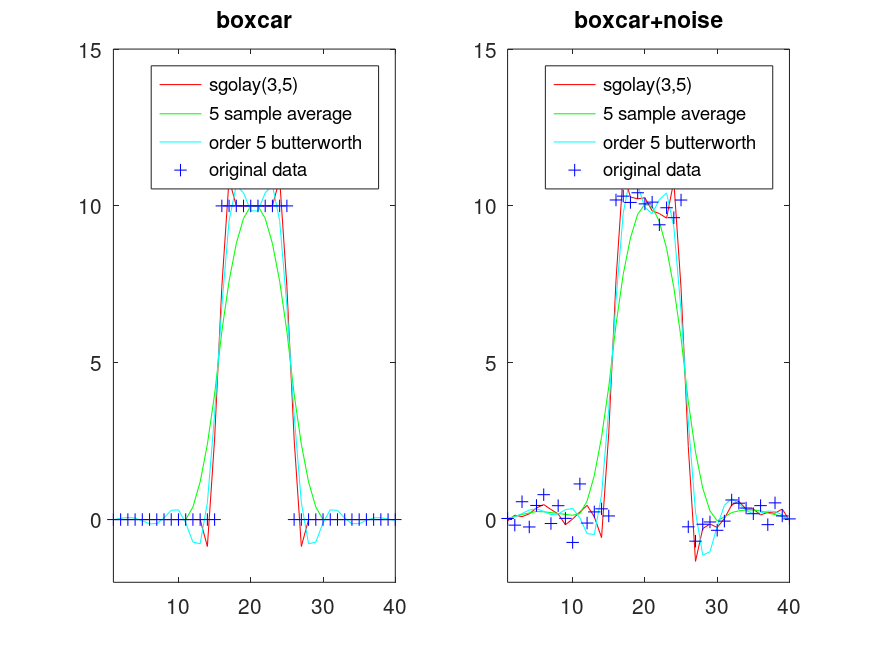Demonstration 2

The following code

 [b, a] = butter(5,1/3);
 t = 0:0.01:1.0;                         % 1 second sample
 x=cos(2*pi*t*3);                        % 3 Hz sinusoid
 subplot(121);
 plot(t,sgolayfilt(x,3,5),"r;sgolay(3,5);",...
      t,filtfilt(ones(1,5)/5,1,x),"g;5 sample average;",...
      t,filtfilt(b,a,x),"c;order 5 butterworth;",...
      t,x,"+b;original data;");
 axis([0 1 -1.5 2.5]);
 title("sinusoid");

 x=x+0.2*randn(size(x));                % signal+noise
 subplot(122);
 plot(t,sgolayfilt(x',3,5),"r;sgolay(3,5);",...
      t,filtfilt(ones(1,5)/5,1,x),"g;5 sample average;",...
      t,filtfilt(b,a,x),"c;order 5 butterworth;",...
      t,x,"+b;original data;");
 axis([0 1 -1.5 2.5]);
 title("sinusoid+noise");

Produces the following figure

Figure 1

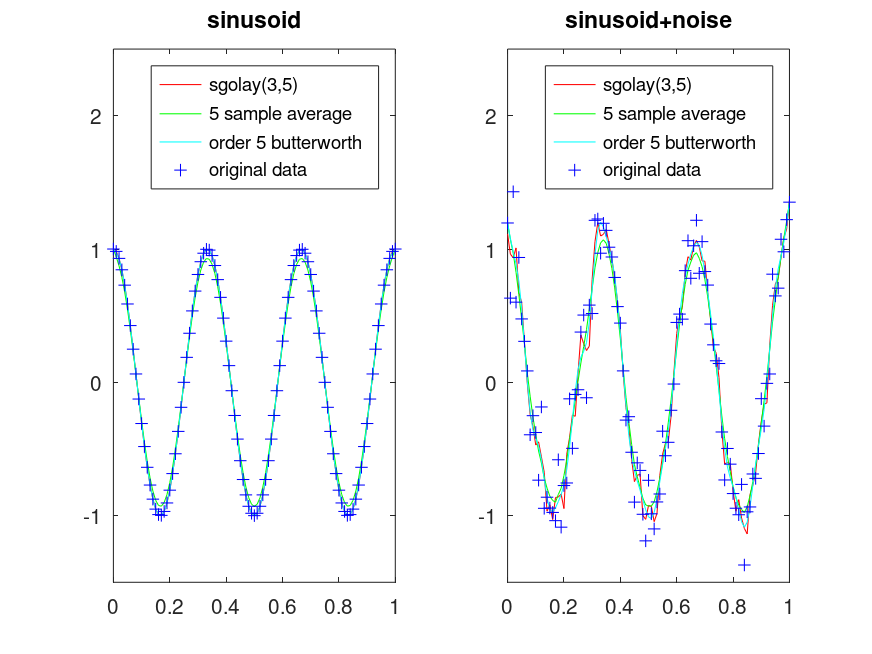Package: signal