- Function File: triang
(m)¶ -
Return the filter coefficients of a triangular window of length m. Unlike the Bartlett window,
triangdoes not go to zero at the edges of the window. For odd m,triang (m)is equal tobartlett (m + 2)except for the zeros at the edges of the window.See also: bartlett.
Demonstration 1
The following code
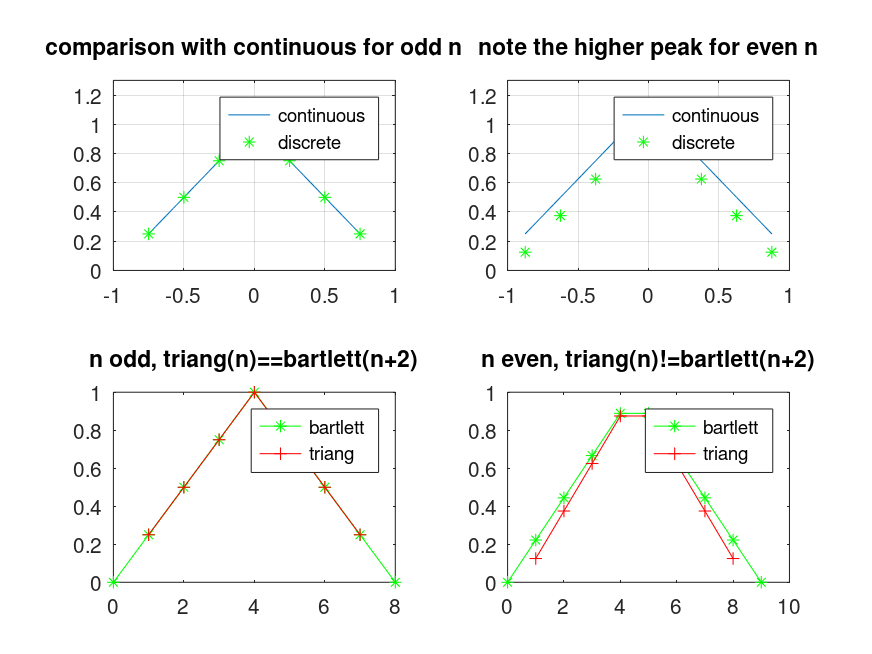
subplot(221);
n=7; k=(n-1)/2; t=[-k:0.1:k]/(k+1);
plot(t,1-abs(t),";continuous;",[-k:k]/(k+1),triang(n),"g*;discrete;");
axis([-1, 1, 0, 1.3]); grid("on");
title("comparison with continuous for odd n");
subplot(222);
n=8; k=(n-1)/2; t=[-k:0.1:k]/(k+1/2);
plot(t,1+1/n-abs(t),";continuous;",[-k:k]/(k+1/2),triang(n),"g*;discrete;");
axis([-1, 1, 0, 1.3]); grid("on");
title("note the higher peak for even n");
subplot(223);
n=7;
plot(0:n+1,bartlett(n+2),"g-*;bartlett;",triang(n),"r-+;triang;");
axis; grid("off");
title("n odd, triang(n)==bartlett(n+2)");
subplot(224);
n=8;
plot(0:n+1,bartlett(n+2),"g-*;bartlett;",triang(n),"r-+;triang;");
axis; grid("off");
title("n even, triang(n)!=bartlett(n+2)");
Produces the following figure
| Figure 1 |
|---|
 |
Package: signal