- Function File: welchwin
(m)¶ - Function File: welchwin
(m, "periodic")¶ - Function File: welchwin
(m, "symmetric")¶ Return the filter coefficients of a Welch window of length m. The Welch window is given by w(n)=1-(n/N-1)^2, n=[0,1, ... m-1]. The optional argument specifies a "symmetric" window (the default) or a "periodic" window.
A symmetric window has zero at each end and maximum in the middle, and the length must be an integer greater than 2. The variable N in the formula above is
(m-1)/2.A periodic window wraps around the cyclic interval [0,1, ... m-1], and is intended for use with the DFT. The length must be an integer greater than 1. The variable N in the formula above is
m/2.See also: blackman, kaiser.
Demonstration 1
The following code
m = 32;
t = [0:m-1];
printf ("Graph: single period of ");
printf ("%d-point periodic (blue) and symmetric (red) windows\n", m);
xp = welchwin (m, "periodic");
xs = welchwin (m, "symmetric");
plot (t, xp, "b", t, xs, "r")
Produces the following output
Graph: single period of 32-point periodic (blue) and symmetric (red) windows
and the following figure
| Figure 1 |
|---|
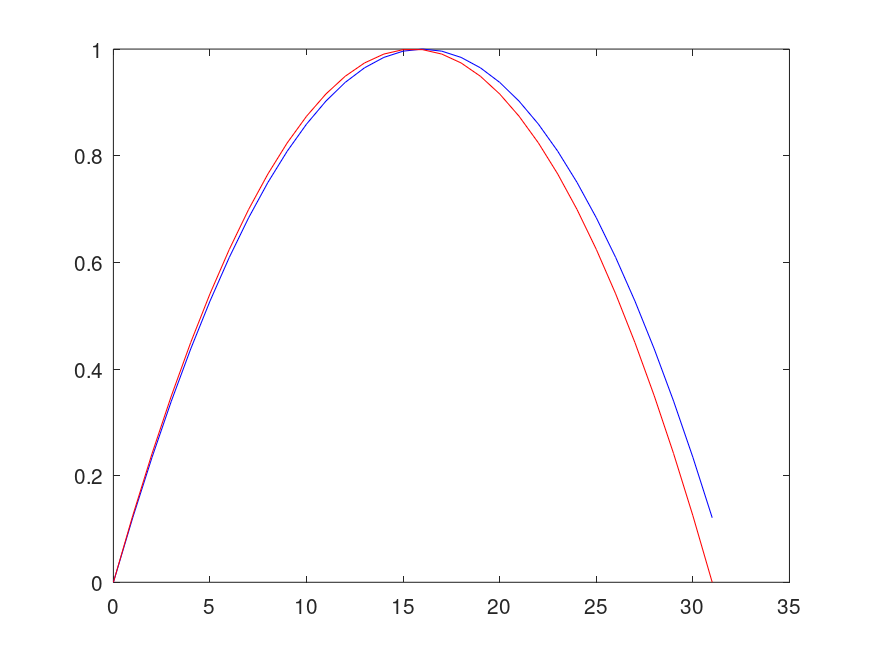 |
Demonstration 2
The following code
m = 32;
t = [0:4*m-1];
printf ("Graph: 4 periods of ");
printf ("%d-point periodic (blue) and symmetric (red) windows\n", m);
xp = welchwin (m, "periodic");
xs = welchwin (m, "symmetric");
xp2 = repmat (xp, 4, 1);
xs2 = repmat (xs, 4, 1);
plot (t, xp2, "b", t, xs2, "r")
Produces the following output
Graph: 4 periods of 32-point periodic (blue) and symmetric (red) windows
and the following figure
| Figure 1 |
|---|
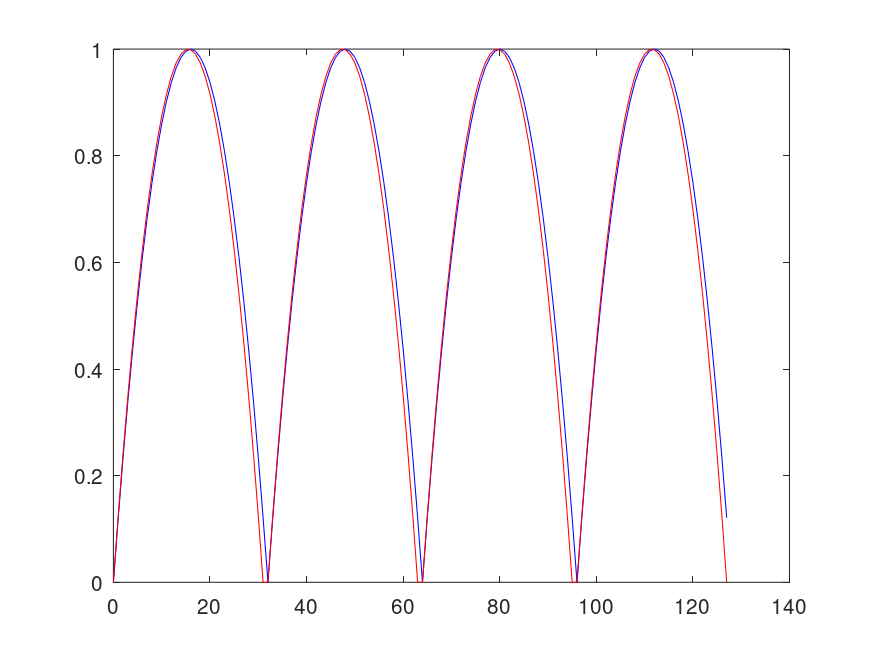 |
Demonstration 3
The following code
m = 32;
n = 512;
xp = welchwin (m, "periodic");
s = fftshift (max (1e-2, abs (fft (postpad (xp, n)))));
f = [-0.5:1/n:0.5-1/n];
printf ("%dx null-padded, power spectrum of %d-point window\n", n/m, m);
semilogy (f, s)
Produces the following output
16x null-padded, power spectrum of 32-point window
and the following figure
| Figure 1 |
|---|
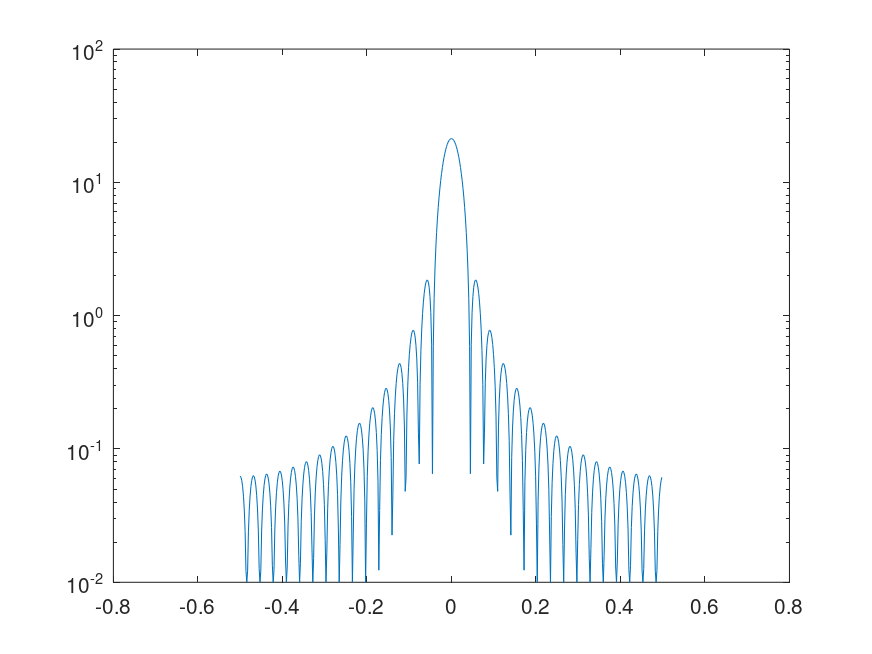 |
Package: signal