- Function File: [dCor, dCov, dVarX, dVarY] = dcov (x, y, index=1)
Distance correlation, covariance and correlation statistics.
It returns distace correlation (dCor), distance covariance (dCov), diatance variace on x (dVarX) and distance variance on y (dVarY).
Reference: https://en.wikipedia.org/wiki/Distance_correlation
See also: corr, cov.
Demonstration 1
The following code
base=@(x) (x- min(x))./(max(x)-min(x));
N = 5e2;
x = randn (N,1); x = base (x);
z = randn (N,1); z = base (z);
# Linear relations
cy = [1 0.55 0.3 0 -0.3 -0.55 -1];
ly = x .* cy;
ly(:,[1:3 5:end]) = base (ly(:,[1:3 5:end]));
# Correlated Gaussian
cz = 1 - abs (cy);
gy = base ( ly + cz.*z);
# Shapes
sx = repmat (x,1,7);
sy = zeros (size (ly));
v = 2 * rand (size(x,1),2) - 1;
sx(:,1) = v(:,1); sy(:,1) = cos(2*pi*sx(:,1)) + 0.5*v(:,2).*exp(-sx(:,1).^2/0.5);
R =@(d) [cosd(d) sind(d); -sind(d) cosd(d)];
tmp = R(35) * v.';
sx(:,2) = tmp(1,:); sy(:,2) = tmp(2,:);
tmp = R(45) * v.';
sx(:,3) = tmp(1,:); sy(:,3) = tmp(2,:);
sx(:,4) = v(:,1); sy(:,4) = sx(:,4).^2 + 0.5*v(:,2);
sx(:,5) = v(:,1); sy(:,5) = 3*sign(v(:,2)).*(sx(:,5)).^2 + v(:,2);
sx(:,6) = cos (2*pi*v(:,1)) + 0.5*(x-0.5);
sy(:,6) = sin (2*pi*v(:,1)) + 0.5*(z-0.5);
sx(:,7) = x + sign(v(:,1)); sy(:,7) = z + sign(v(:,2));
sy = base (sy);
sx = base (sx);
# scaled shape
sc = 1/3;
ssy = (sy-0.5) * sc + 0.5;
n = size (ly,2);
ym = 1.2;
xm = 0.5;
fmt={'horizontalalignment','center'};
ff = "% .2f";
figure (1)
for i=1:n
subplot(4,n,i);
plot (x, gy(:,i), '.b');
axis tight
axis off
text (xm,ym,sprintf (ff, dcov (x,gy(:,i))),fmt{:})
subplot(4,n,i+n);
plot (x, ly(:,i), '.b');
axis tight
axis off
text (xm,ym,sprintf (ff, dcov (x,ly(:,i))),fmt{:})
subplot(4,n,i+2*n);
plot (sx(:,i), sy(:,i), '.b');
axis tight
axis off
text (xm,ym,sprintf (ff, dcov (sx(:,i),sy(:,i))),fmt{:})
v = axis ();
subplot(4,n,i+3*n);
plot (sx(:,i), ssy(:,i), '.b');
axis (v)
axis off
text (xm,ym,sprintf (ff, dcov (sx(:,i),ssy(:,i))),fmt{:})
endfor
Produces the following figure
| Figure 1 |
|---|
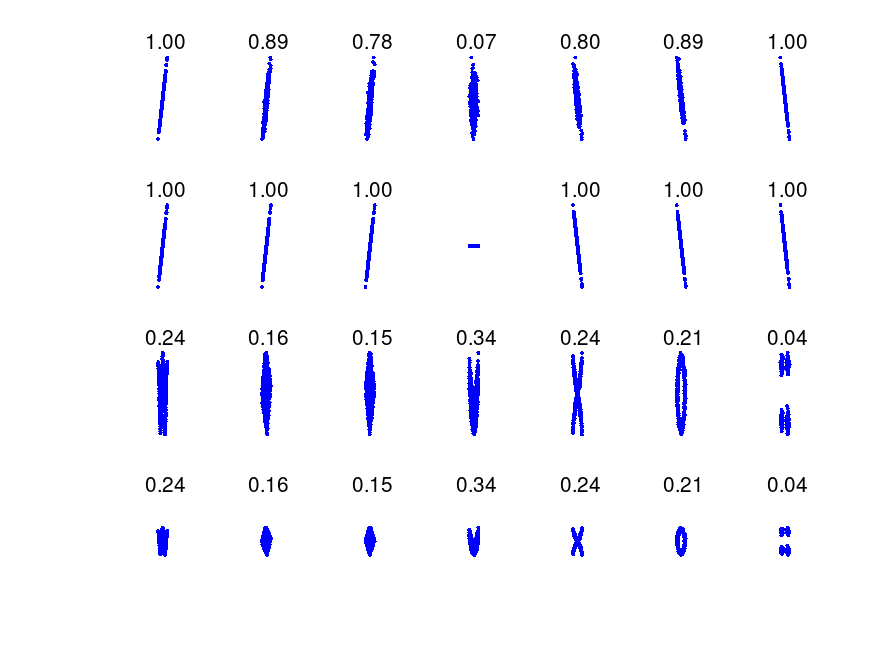 |
Package: statistics