- Function File: jackstat = jackknife (E, x, …)
Compute jackknife estimates of a parameter taking one or more given samples as parameters. In particular, E is the estimator to be jackknifed as a function name, handle, or inline function, and x is the sample for which the estimate is to be taken. The i-th entry of jackstat will contain the value of the estimator on the sample x with its i-th row omitted.
jackstat(i) = E(x(1 : i - 1, i + 1 : length(x)))
Depending on the number of samples to be used, the estimator must have the appropriate form: If only one sample is used, then the estimator need not be concerned with cell arrays, for example jackknifing the standard deviation of a sample can be performed with
jackstat = jackknife (@std, rand (100, 1)). If, however, more than one sample is to be used, the samples must all be of equal size, and the estimator must address them as elements of a cell-array, in which they are aggregated in their order of appearance:jackstat = jackknife(@(x) std(x{1})/var(x{2}), rand (100, 1), randn (100, 1)If all goes well, a theoretical value P for the parameter is already known, n is the sample size,
t = n * E(x) - (n - 1) * mean(jackstat), andv = sumsq(n * E(x) - (n - 1) * jackstat - t) / (n * (n - 1)), then(t-P)/sqrt(v)should follow a t-distribution with n-1 degrees of freedom.Jackknifing is a well known method to reduce bias; further details can be found in:
- Rupert G. Miller: The jackknife-a review; Biometrika (1974) 61(1): 1-15; doi:10.1093/biomet/61.1.1
- Rupert G. Miller: Jackknifing Variances; Ann. Math. Statist. Volume 39, Number 2 (1968), 567-582; doi:10.1214/aoms/1177698418
- M. H. Quenouille: Notes on Bias in Estimation; Biometrika Vol. 43, No. 3/4 (Dec., 1956), pp. 353-360; doi:10.1093/biomet/43.3-4.353
Demonstration 1
The following code
for k = 1:1000 x=rand(10,1); s(k)=std(x); jackstat=jackknife(@std,x); j(k)=10*std(x) - 9*mean(jackstat); end figure();hist([s',j'], 0:sqrt(1/12)/10:2*sqrt(1/12))
Produces the following figure
| Figure 1 |
|---|
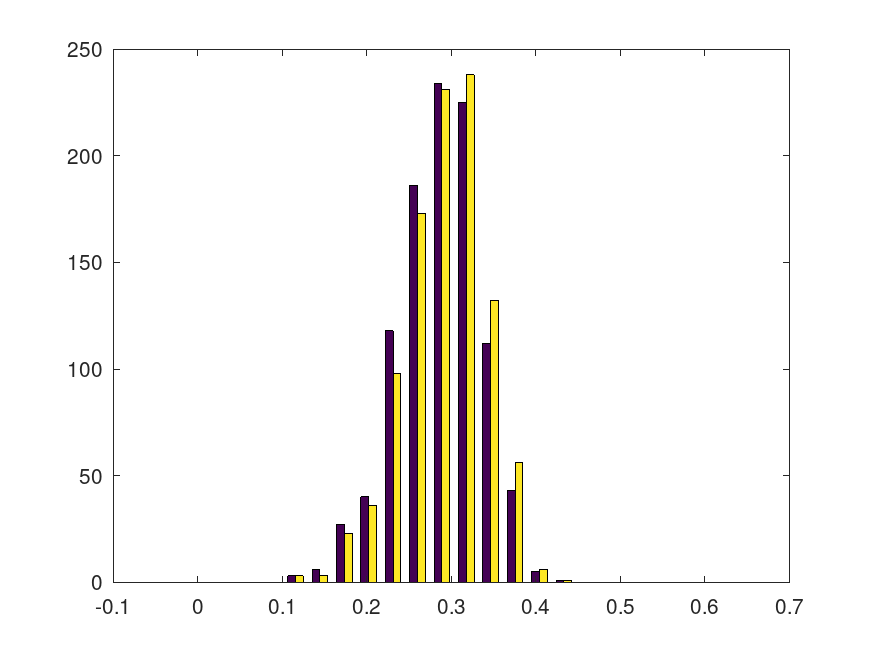 |
Demonstration 2
The following code
for k = 1:1000
x=randn(1,50);
y=rand(1,50);
jackstat=jackknife(@(x) std(x{1})/std(x{2}),y,x);
j(k)=50*std(y)/std(x) - 49*mean(jackstat);
v(k)=sumsq((50*std(y)/std(x) - 49*jackstat) - j(k)) / (50 * 49);
end
t=(j-sqrt(1/12))./sqrt(v);
figure();plot(sort(tcdf(t,49)),"-;Almost linear mapping indicates good fit with t-distribution.;")
Produces the following figure
| Figure 1 |
|---|
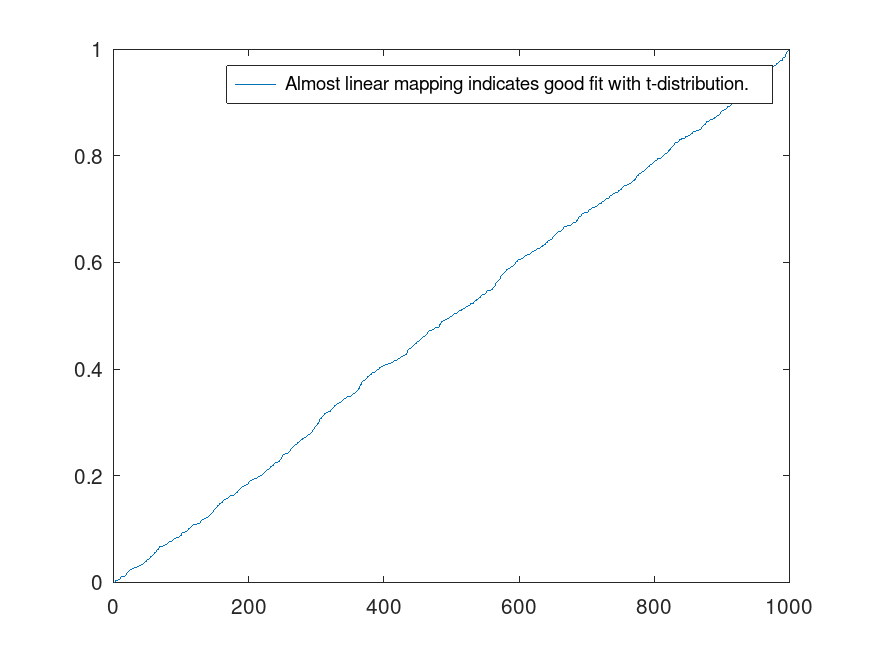 |
Package: statistics