Function File: y = mvnpdf (x)

Function File: y = mvnpdf (x, mu)

Function File: y = mvnpdf (x, mu, sigma)

Compute multivariate normal pdf for x given mean mu and covariance matrix sigma. The dimension of x is d x p, mu is 1 x p and sigma is p x p. The normal pdf is defined as

1/y^2 = (2 pi)^p |Sigma|exp { (x-mu)' inv(Sigma) (x-mu) }

References

NIST Engineering Statistics Handbook 6.5.4.2 http://www.itl.nist.gov/div898/handbook/pmc/section5/pmc542.htm

Algorithm

Using Cholesky factorization on the positive definite covariance matrix:

r = chol (sigma);

where r’*r = sigma. Being upper triangular, the determinant of r is trivially the product of the diagonal, and the determinant of sigma is the square of this:

det = prod (diag (r))^2;

The formula asks for the square root of the determinant, so no need to square it.

The exponential argument A = x’ * inv (sigma) * x

A = x' * inv (sigma) * x
  = x' * inv (r' * r) * x
  = x' * inv (r) * inv(r') * x

Given that inv (r’) == inv(r)’, at least in theory if not numerically,

A  = (x' / r) * (x'/r)' = sumsq (x'/r)

The interface takes the parameters to the multivariate normal in columns rather than rows, so we are actually dealing with the transpose:

A = sumsq (x/r)

and the final result is:

r = chol (sigma)
y = (2*pi)^(-p/2) * exp (-sumsq ((x-mu)/r, 2)/2) / prod (diag (r))

See also: mvncdf, mvnrnd.

Demonstration 1

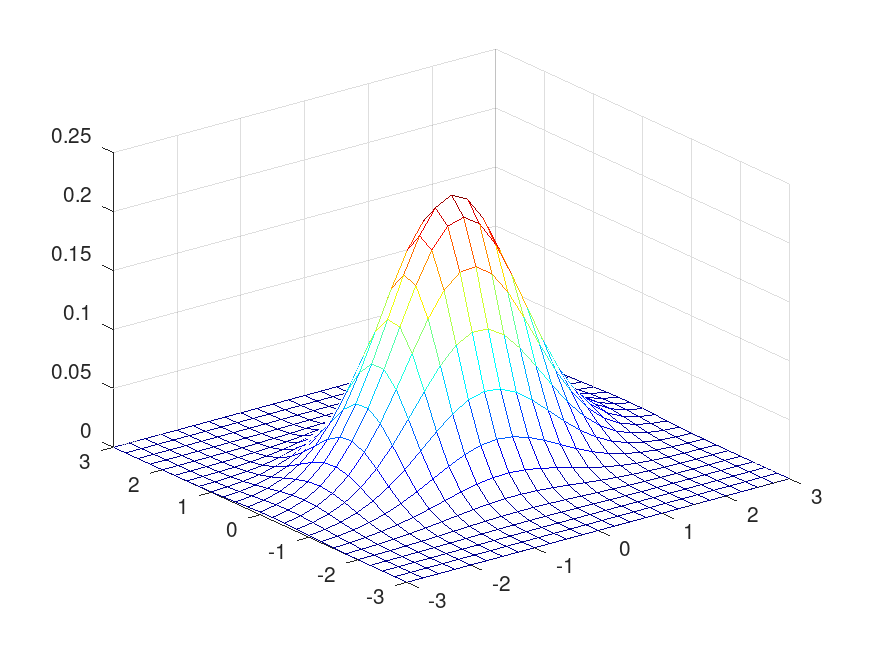Package: statistics