- Function File: [m, K] = regress_gp (x, y, Sp)
- Function File: [… yi dy] = regress_gp (…, xi)
Linear scalar regression using gaussian processes.
It estimates the model y = x’*m for x R^D and y in R. The information about errors of the predictions (interpolation/extrapolation) is given by the covarianve matrix K. If D==1 the inputs must be column vectors, if D>1 then x is n-by-D, with n the number of data points. Sp defines the prior covariance of m, it should be a (D+1)-by-(D+1) positive definite matrix, if it is empty, the default is
Sp = 100*eye(size(x,2)+1).If xi inputs are provided, the model is evaluated and returned in yi. The estimation of the variation of yi are given in dy.
Run
demo regress_gpto see an examples.The function is a direc implementation of the formulae in pages 11-12 of Gaussian Processes for Machine Learning. Carl Edward Rasmussen and Christopher K. I. Williams. The MIT Press, 2006. ISBN 0-262-18253-X. available online at http://gaussianprocess.org/gpml/.
See also: regress.
Demonstration 1
The following code
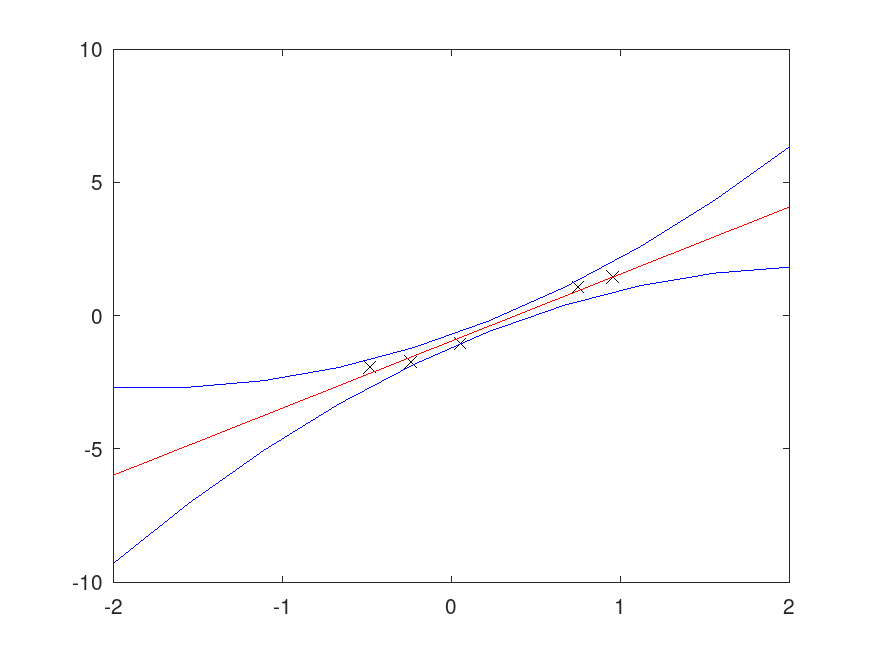
% 1D Data x = 2*rand (5,1)-1; y = 2*x -1 + 0.3*randn (5,1); % Points for interpolation/extrapolation xi = linspace (-2,2,10)'; [m K yi dy] = regress_gp (x,y,[],xi); plot (x,y,'xk',xi,yi,'r-',xi,bsxfun(@plus, yi, [-dy +dy]),'b-');
Produces the following figure
| Figure 1 |
|---|
 |
Demonstration 2
The following code
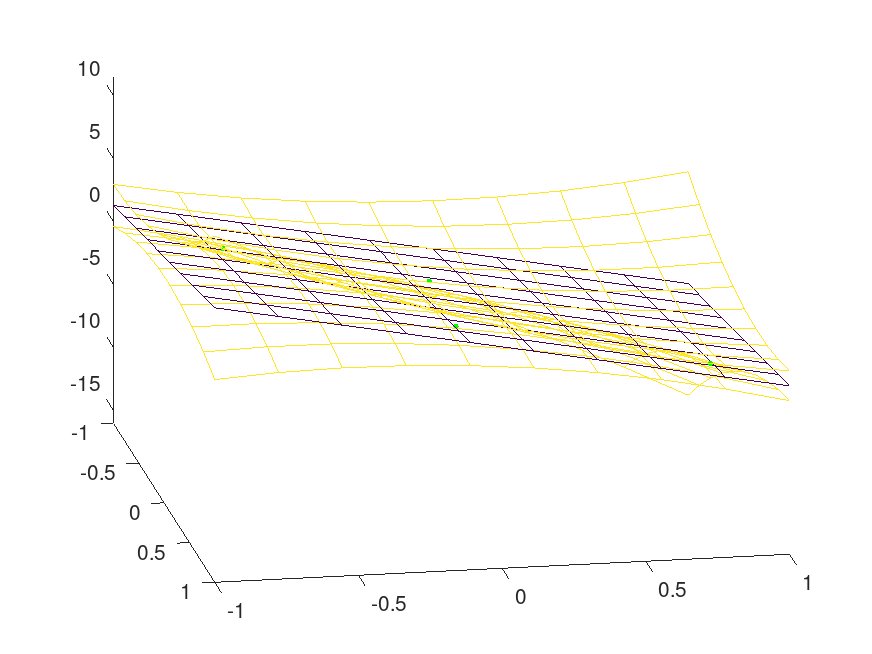
% 2D Data x = 2*rand (4,2)-1; y = 2*x(:,1)-3*x(:,2) -1 + 1*randn (4,1); % Mesh for interpolation/extrapolation [xi yi] = meshgrid (linspace (-1,1,10)); [m K zi dz] = regress_gp (x,y,[],[xi(:) yi(:)]); zi = reshape (zi, 10,10); dz = reshape (dz,10,10); plot3 (x(:,1),x(:,2),y,'.g','markersize',8); hold on; h = mesh (xi,yi,zi,zeros(10,10)); set(h,'facecolor','none'); h = mesh (xi,yi,zi+dz,ones(10,10)); set(h,'facecolor','none'); h = mesh (xi,yi,zi-dz,ones(10,10)); set(h,'facecolor','none'); hold off axis tight view(80,25)
Produces the following figure
| Figure 1 |
|---|
 |
Demonstration 3
The following code
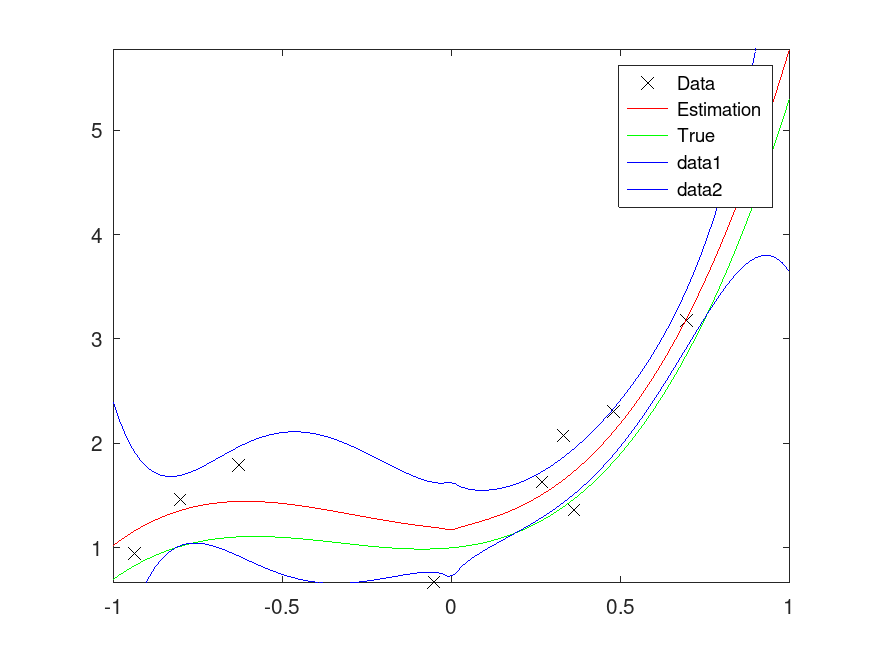
% Projection over basis function pp = [2 2 0.3 1]; n = 10; x = 2*rand (n,1)-1; y = polyval(pp,x) + 0.3*randn (n,1); % Powers px = [sqrt(abs(x)) x x.^2 x.^3]; % Points for interpolation/extrapolation xi = linspace (-1,1,100)'; pxi = [sqrt(abs(xi)) xi xi.^2 xi.^3]; Sp = 100*eye(size(px,2)+1); Sp(2,2) = 1; # We don't believe the sqrt is present [m K yi dy] = regress_gp (px,y,Sp,pxi); disp(m) plot (x,y,'xk;Data;',xi,yi,'r-;Estimation;',xi,polyval(pp,xi),'g-;True;'); axis tight axis manual hold on plot (xi,bsxfun(@plus, yi, [-dy +dy]),'b-'); hold off
Produces the following output
1.1572 0.1989 0.2314 2.0433 2.1448
and the following figure
| Figure 1 |
|---|
 |
Package: statistics