- : pts = sigma_pts (n)
- pts =: sigma_pts (n, m)
- pts =: sigma_pts (n, m, K)
- pts =: sigma_pts (n, m, K, l)
Calculates 2*n+1 sigma points in n dimensions.
Sigma points are used in the unscented transfrom to estimate the result of applying a given nonlinear transformation to a probability distribution that is characterized only in terms of a finite set of statistics.
If only the dimension n is given the resulting points have zero mean and identity covariance matrix. If the mean m or the covaraince matrix K are given, then the resulting points will have those statistics. The factor l scaled the points away from the mean. It is useful to tune the accuracy of the unscented transfrom.
There is no unique way of computing sigma points, this function implements the algorithm described in section 2.6 "The New Filter" pages 40-41 of
Uhlmann, Jeffrey (1995). "Dynamic Map Building and Localization: New Theoretical Foundations". Ph.D. thesis. University of Oxford.
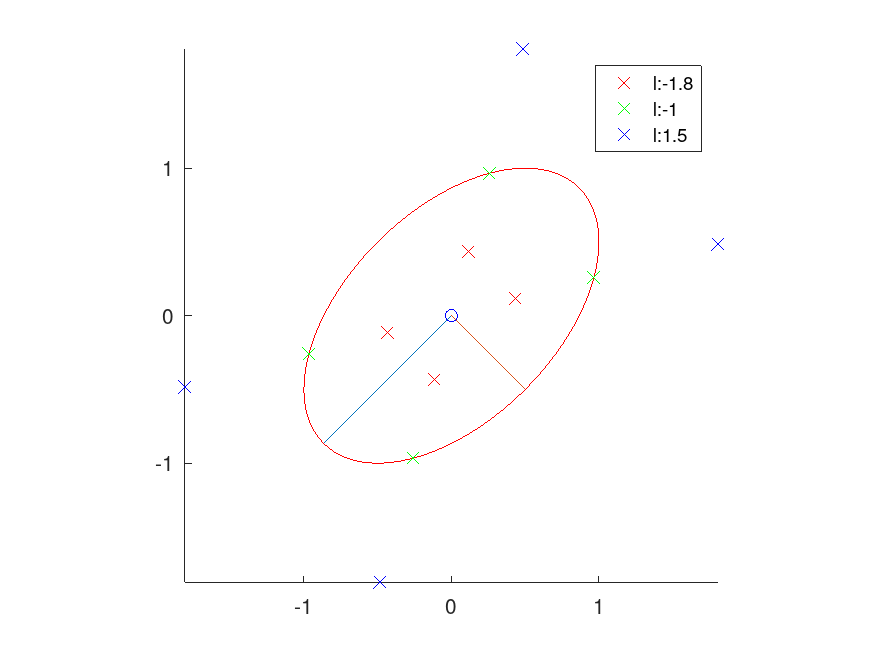
Demonstration 1
The following code
K = [1 0.5; 0.5 1]; # covaraince matrix
# calculate and build associated ellipse
[R,S,~] = svd (K);
theta = atan2 (R(2,1), R(1,1));
v = sqrt (diag (S));
v = v .* [cos(theta) sin(theta); -sin(theta) cos(theta)];
t = linspace (0, 2*pi, 100).';
xe = v(1,1) * cos (t) + v(2,1) * sin (t);
ye = v(1,2) * cos (t) + v(2,2) * sin (t);
figure(1); clf; hold on
# Plot ellipse and axes
line ([0 0; v(:,1).'],[0 0; v(:,2).'])
plot (xe,ye,'-r');
col = 'rgb';
l = [-1.8 -1 1.5];
for li = 1:3
p = sigma_pts (2, [], K, l(li));
tmp = plot (p(2:end,1), p(2:end,2), ['x' col(li)], ...
p(1,1), p(1,2), ['o' col(li)]);
h(li) = tmp(1);
endfor
hold off
axis image
legend (h, arrayfun (@(x) sprintf ("l:%.2g", x), l, "unif", 0));
Produces the following figure
| Figure 1 |
|---|
 |
Package: statistics