- Function File:
output =boxcount(S)¶ - Function File:
output =boxcount(S, paramName, paramValue, …)¶ -
Estimates the Renyi entropy of Qth order using a partition of the phase space instead of using the Grassberger-Procaccia scheme.
The program also can handle multivariate data, so that the phase space is build of the components of the time series plus a temporal embedding, if desired. Also, note that the memory requirement does not increase exponentially like 1/epsilon^M but only like M*(length of series). So it can also be used for small epsilon and large M. No finite sample corrections are implemented so far.
Input
- S
This function always assumes that each time series is along the longer dimension of matrix S. It also assumes that every dimension (counting along the shorter dimension) of S is considered a component of the time series.
Parameters
- m
The maximum embedding dimension [default = 10].
- d
The delay used [default = 1].
- q
Order of the entropy [default = 2.0].
- rlow
Minimum length scale [default = 1e-3].
- rhigh
Maximum length scale [default = 1].
- eps_no
Number of length scale values [default = 20].
Output
The output is alligned with the input. If the input components where column vectors then the output is a maximum-embedding-dimension x number-of-components struct array with the following fields:
- dim
Holds the embedding dimension of the struct.
- entropy
The entropy output. Contains three columns which hold:
- epsilon
- Qth order entropy (Hq (dimension,epsilon))
- Qth order differential entropy (Hq (dimension,epsilon) - Hq (dimension-1,epsilon))
See also: demo boxcount, d2, c1.
Algorithms
The algorithms for this functions have been taken from the TISEAN package.
Demonstration 1
The following code
res = boxcount (henon (1000),'m',5);
do_plot_entrop = @(x) semilogx (x{1}(:,1),x{1}(:,3),'g');
hold on
# Show only for first component
arrayfun (do_plot_entrop, {res(:,1).entropy});
hold off
axis tight
xlabel ("Epsilon")
ylabel ("Differential Entropies");
title ("Entropies")
Produces the following figure
| Figure 1 |
|---|
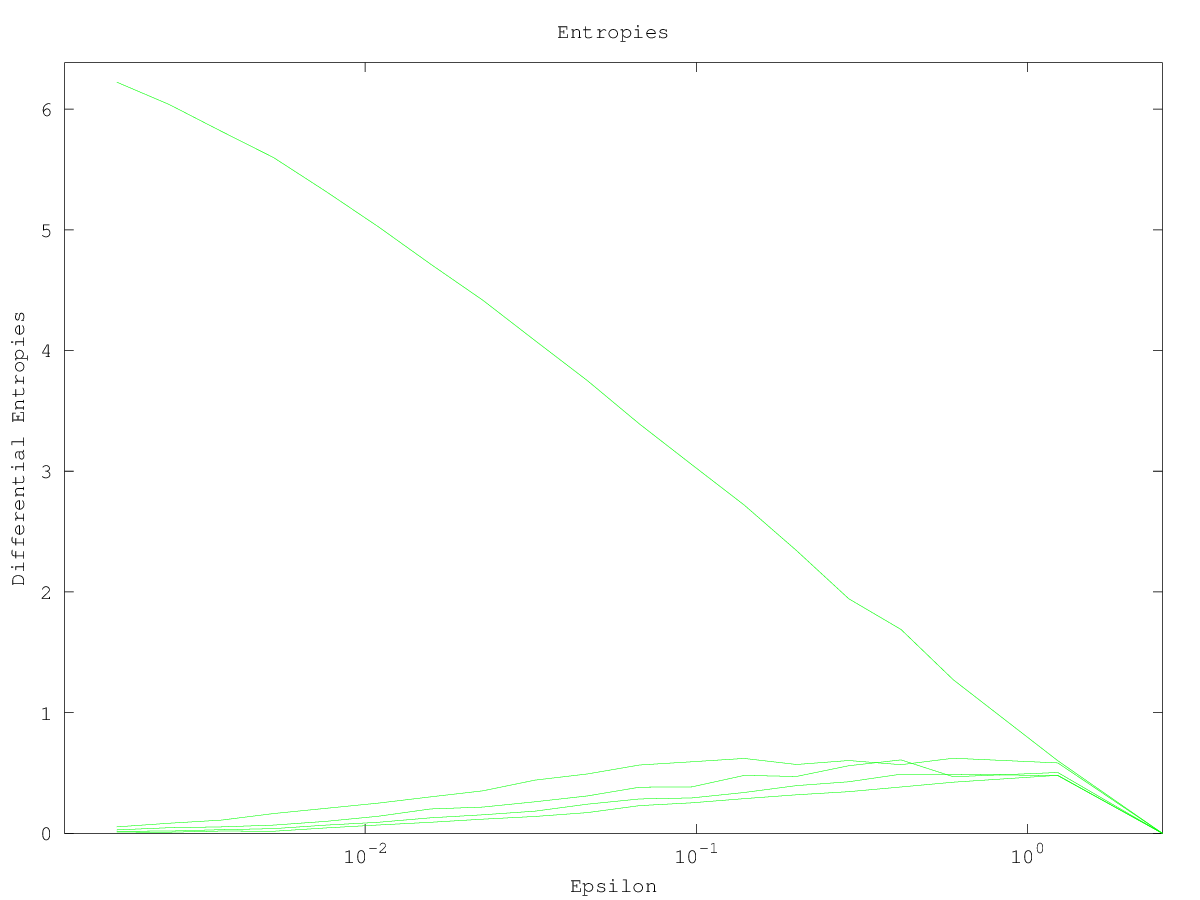 |
Package: tisean