Navigation

Operators and Keywords

Function List:

C++ API

Function File: output = c2g (d2_out)

This program calculates the Gaussian kernel correlation integral and its logarithmic derivatice from correlation sums calculated by d2 (the ’c2’ field of the d2 output).

It uses the following formula to calculate the Gaussian kernel correlation integral: 

             /00            2
         1   |       /    x   \
C (r) = ---  |dx exp |- ----- |x C(x)
 G        2  |       \     2  /
         r   /0           2r

And the logarithmic derivative is calculated using: 

           d
D (r) = ------- log C (r)
 G      d log r      G

Input

The input needs to be the output of d2.

Output

The output is a struct array of the same length as the input. It contains the following fiels:

dim

The dimension for each matrix g.

g

Matrix with three columns. The first contains epsilon (the first column of field ’c2’ from the d2 output), the second is the Gaussian kernel correlation integral and the third its logarithmic derivative.

See also: demo c2g, d2, c2t, av_d2.

Algorithms

The algorithms for this functions have been taken from the TISEAN package.

Demonstration 1

The following code

 vals          = d2 (henon (5000), 'd', 1, 't', 50);
 kernel        = c2g (vals);
 do_plot_slope = @(x) semilogx (x{1}(:,1),x{1}(:,3),'r');
 hold on
 arrayfun (do_plot_slope, {kernel.g});
 hold off
 axis tight
 xlabel ("Epsilon")
 ylabel ("logarithmic derivative")
 title ("Gaussian kernel");

Produces the following figure

Figure 1

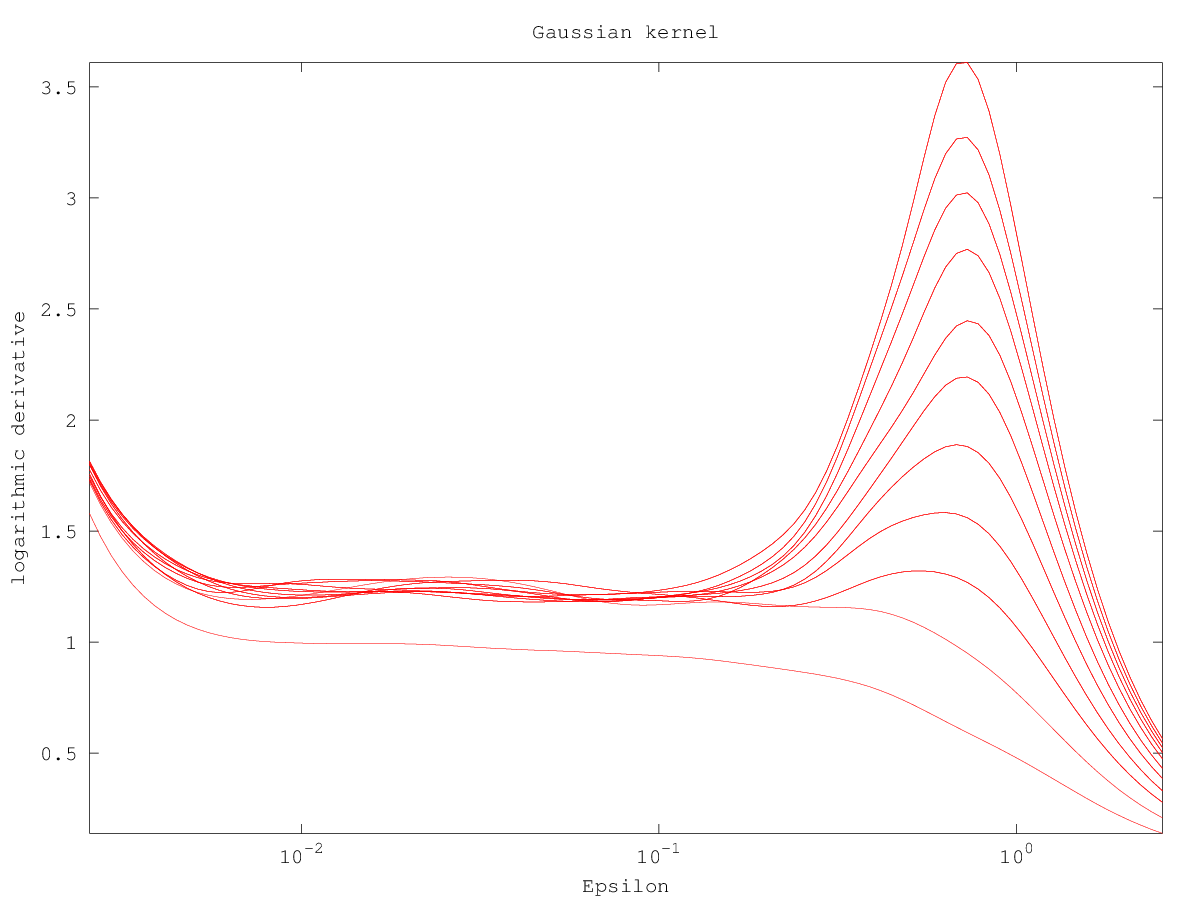Package: tisean