Navigation

Operators and Keywords

Function List:

C++ API

Function File: phi = ls_extract_solution (t, d, phi0, f)

Calculate a level-set function of an evolving geometry from the result of ls_solve_stationary. In particular, it is assumed that d = ls_solve_stationary (phi0, f, h). phi is set to a level-set function for the evolved geometry at time t. The zero level-set of phi will describe the same geometry as the solution of the level-set equation 

d/dt phi + f |grad phi |= 0,

although phi will not be the full solution to this equation.

See also: ls_solve_stationary, ls_time_step, ls_animate_evolution.

Demonstration 1

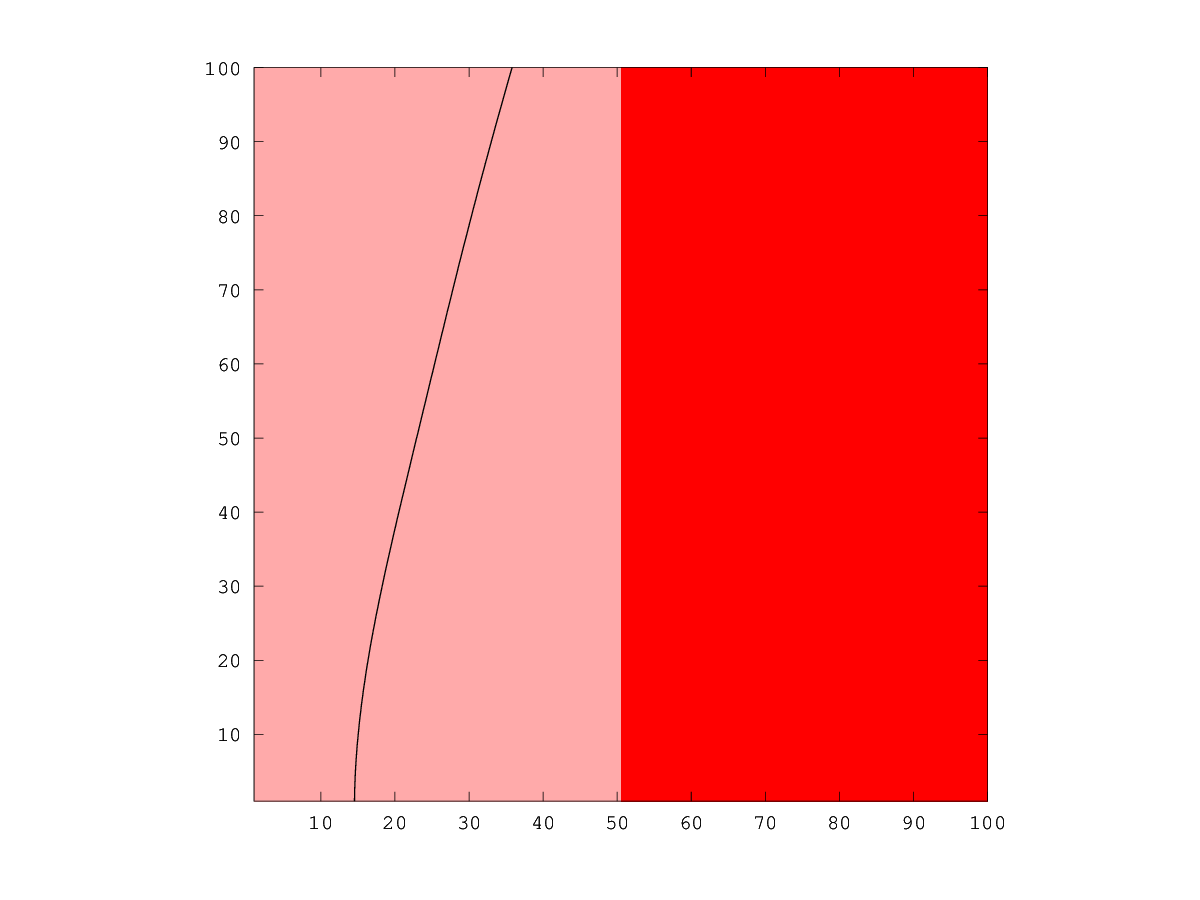
The following code

  n = 100;
  x = linspace (-10, 10, n);
  h = x(2) - x(1);
  [XX, YY] = meshgrid (x, x);

  phi = ls_genbasic (XX, YY, "half", [5, -10], [1, -1]);
  f = sign (XX) + 2;

  times = linspace (1, 9, 80);
  ls_animate_evolution (phi, f, h, times, 0.05);

Produces the following figure

Figure 1

Demonstration 2

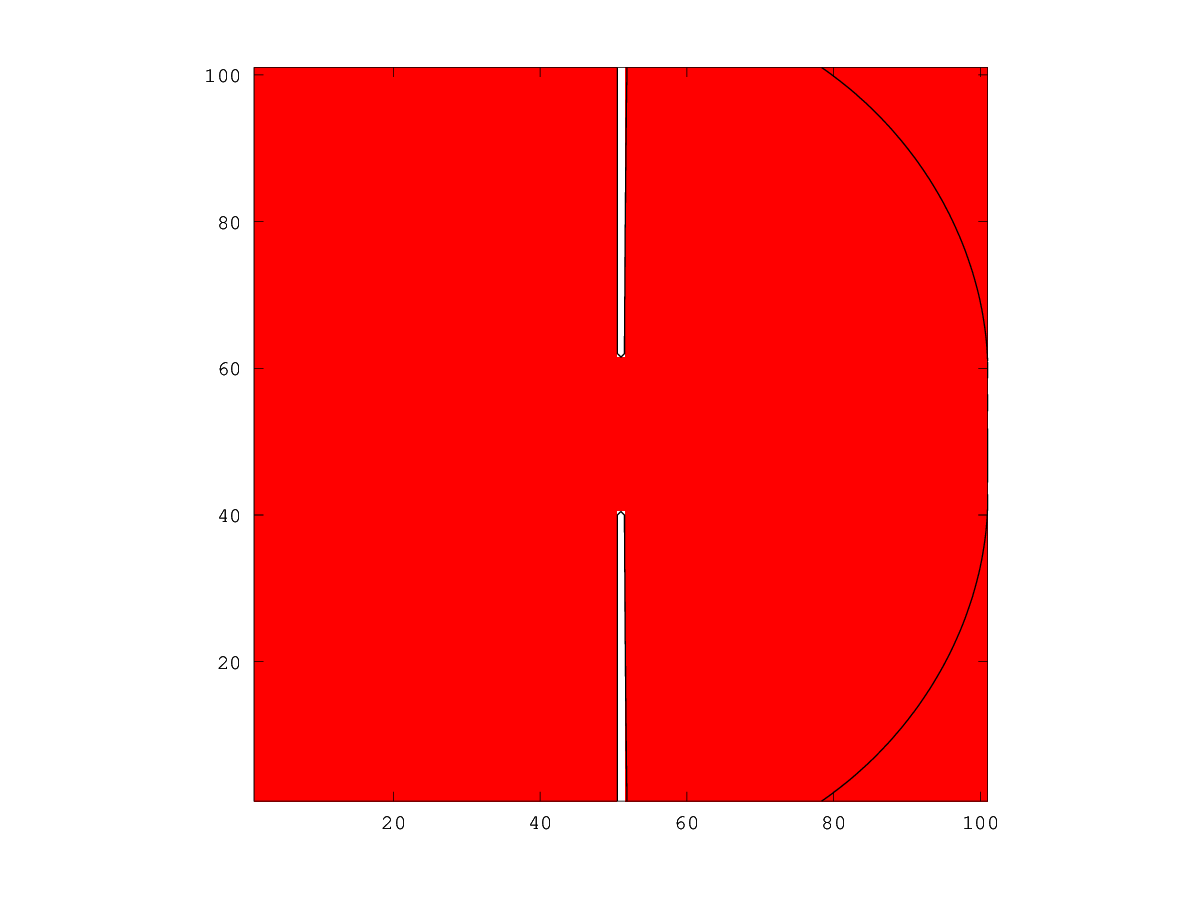
The following code

  n = 101;
  x = linspace (-10, 10, n);
  h = x(2) - x(1);
  [XX, YY] = meshgrid (x, x);

  phi = ls_genbasic (XX, YY, "half", [-9, 0], [-1, 0]);
  f = ones (size (phi));
  f(XX == 0 & abs (YY) > 2) = 0;

  times = linspace (1, 19, 80);
  ls_animate_evolution (phi, f, h, times, 0.05);

Produces the following figure

Figure 1

Demonstration 3

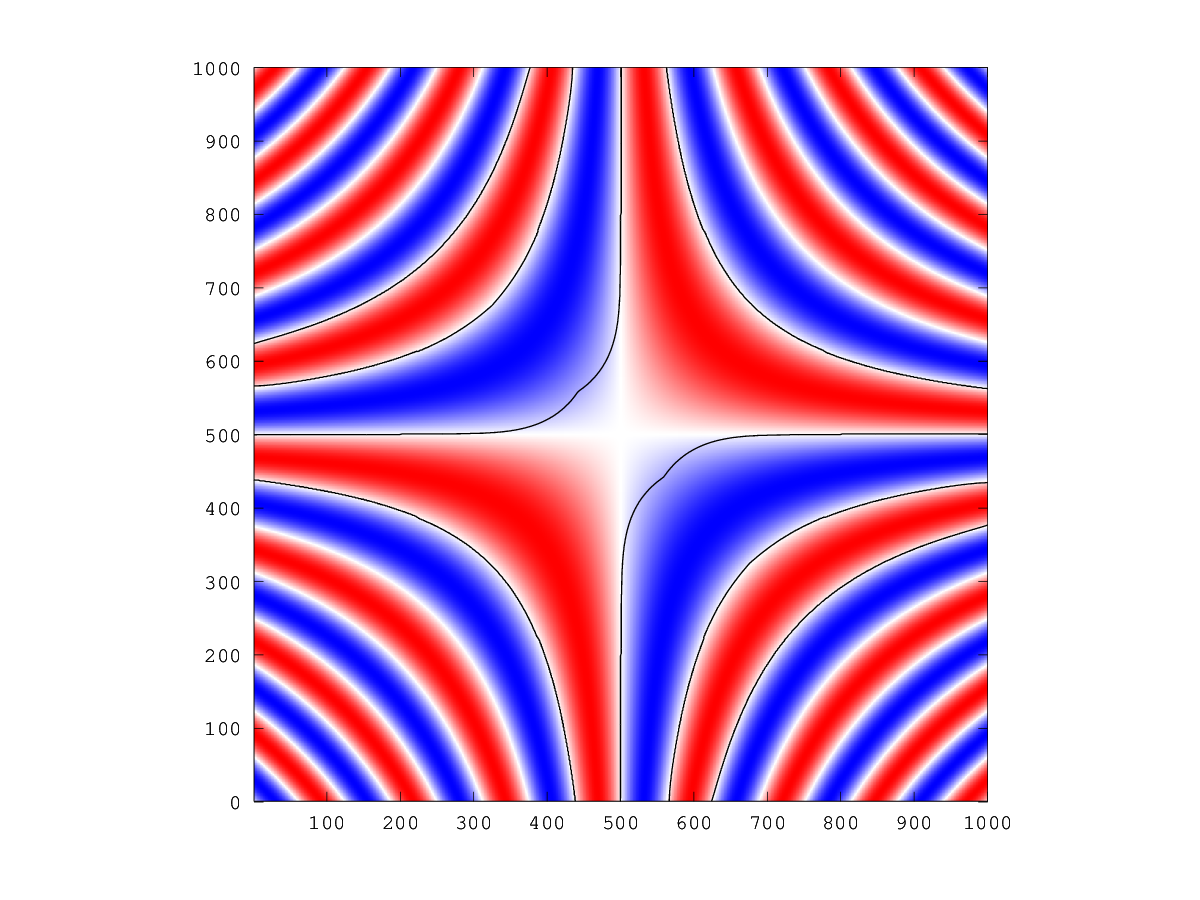
The following code

  n = 1000;
  x = linspace (-5, 5, n);
  h = x(2) - x(1);
  [XX, YY] = meshgrid (x, x);

  F = sin (XX .* YY);
  phi0 = ls_genbasic (XX, YY, "sphere", [0, 0], 3);
  ls_animate_evolution (phi0, F, h, linspace (0, 3, 40), 0.01);

Produces the following figure

Figure 1

Package: level-set